We prove the longstanding physics conjecture that there exists a unique two-parameter 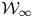${\mathcal {W}}_{\infty }$-algebra which is freely generated of type 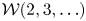${\mathcal {W}}(2,3,\ldots )$, and generated by the weights 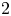$2$ and 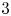$3$ fields. Subject to some mild constraints, all vertex algebras of type 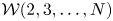${\mathcal {W}}(2,3,\ldots , N)$ for some 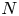$N$ can be obtained as quotients of this universal algebra. As an application, we show that for 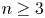$n\geq 3$, the structure constants for the principal 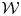${\mathcal {W}}$-algebras 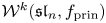${\mathcal {W}}^k({\mathfrak s}{\mathfrak l}_n, f_{\text {prin}})$ are rational functions of 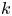$k$ and 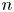$n$, and we classify all coincidences among the simple quotients 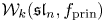${\mathcal {W}}_k({\mathfrak s}{\mathfrak l}_n, f_{\text {prin}})$ for $n\geq 2$. 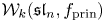We also obtain many new coincidences between ${\mathcal {W}}_k({\mathfrak s}{\mathfrak l}_n, f_{\text {prin}})$ and other vertex algebras of type 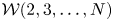${\mathcal {W}}(2,3,\ldots , N)$ which arise as cosets of affine vertex algebras or nonprincipal ${\mathcal {W}}$-algebras.

Simple, or Kleinian, singularities are classified by Dynkin diagrams of type $ADE$. Let $\mathfrak {g}$ be the corresponding finite-dimensional Lie algebra, and $W$ its Weyl group. The set of $\mathfrak {g}$-invariants in the basic representation of the affine Kac–Moody algebra $\hat {\mathfrak {g}}$ is known as a $\mathcal {W}$-algebra and is a subalgebra of the Heisenberg vertex algebra $\mathcal {F}$. Using period integrals, we construct an analytic continuation of the twisted representation of $\mathcal {F}$. Our construction yields a global object, which may be called a $W$-twisted representation of $\mathcal {F}$. Our main result is that the total descendant potential of the singularity, introduced by Givental, is a highest-weight vector for the $\mathcal {W}$-algebra.