The Banach spaces 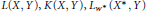 $L(X,Y),K(X,Y),{{L}_{{{w}^{*}}}}({{X}^{*}},Y)$, and
$L(X,Y),K(X,Y),{{L}_{{{w}^{*}}}}({{X}^{*}},Y)$, and 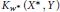 ${{K}_{{{w}^{*}}}}({{X}^{*}},Y)$ are studied to determine when they contain the classical Banach spaces
${{K}_{{{w}^{*}}}}({{X}^{*}},Y)$ are studied to determine when they contain the classical Banach spaces 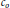 ${{c}_{o}}$ or
${{c}_{o}}$ or 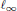 ${{l}_{\infty }}$. The complementation of the Banach space
${{l}_{\infty }}$. The complementation of the Banach space 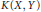 $K(X,Y)$ in
$K(X,Y)$ in 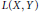 $L(X,Y)$ is discussed as well as what impact this complementation has on the embedding of
$L(X,Y)$ is discussed as well as what impact this complementation has on the embedding of 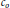 ${{c}_{o}}$ or
${{c}_{o}}$ or 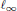 ${{l}_{\infty }}$ in
${{l}_{\infty }}$ in 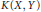 $K(X,Y)$ or
$K(X,Y)$ or 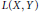 $L(X,Y)$. Results of Kalton, Feder, and Emmanuele concerning the complementation of
$L(X,Y)$. Results of Kalton, Feder, and Emmanuele concerning the complementation of 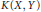 $K(X,Y)$ in
$K(X,Y)$ in 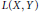 $L(X,Y)$ are generalized. Results concerning the complementation of the Banach space
$L(X,Y)$ are generalized. Results concerning the complementation of the Banach space 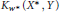 ${{K}_{{{w}^{*}}}}({{X}^{*}},Y)$ in
${{K}_{{{w}^{*}}}}({{X}^{*}},Y)$ in 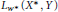 ${{L}_{{{w}^{*}}}}({{X}^{*}},Y)$ are also explored as well as how that complementation affects the embedding of
${{L}_{{{w}^{*}}}}({{X}^{*}},Y)$ are also explored as well as how that complementation affects the embedding of 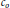 ${{c}_{o}}$ or
${{c}_{o}}$ or 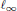 ${{l}_{\infty }}$ in
${{l}_{\infty }}$ in 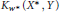 ${{K}_{{{w}^{*}}}}({{X}^{*}},Y)$ or
${{K}_{{{w}^{*}}}}({{X}^{*}},Y)$ or 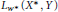 ${{L}_{{{w}^{*}}}}({{X}^{*}},Y)$. The
${{L}_{{{w}^{*}}}}({{X}^{*}},Y)$. The 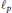 ${{l}_{p}}$ spaces for
${{l}_{p}}$ spaces for 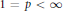 $1\,=\,p\,<\,\infty $ are studied to determine when the space of compact operators from one
$1\,=\,p\,<\,\infty $ are studied to determine when the space of compact operators from one 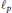 ${{l}_{p}}$ space to another contains
${{l}_{p}}$ space to another contains 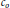 ${{c}_{o}}$. The paper contains a new result which classifies these spaces of operators. A new result using vector measures is given to provide more efficient proofs of theorems by Kalton, Feder, Emmanuele, Emmanuele and John, and Bator and Lewis.
${{c}_{o}}$. The paper contains a new result which classifies these spaces of operators. A new result using vector measures is given to provide more efficient proofs of theorems by Kalton, Feder, Emmanuele, Emmanuele and John, and Bator and Lewis.