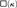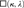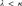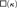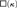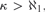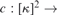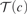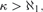With the help of various square principles, we obtain results concerning the consistency strength of several statements about trees containing ascent paths, special trees, and strong chain conditions. Building on a result that shows that Todorčević’s principle $\square \left( {\kappa ,\lambda } \right)$ implies an indexed version of $\square \left( {\kappa ,\lambda } \right)$, we show that for all infinite, regular cardinals $\lambda < \kappa$, the principle $\square \left( \kappa \right)$ implies the existence of a κ-Aronszajn tree containing a λ-ascent path. We then provide a complete picture of the consistency strengths of statements relating the interactions of trees with ascent paths and special trees. As a part of this analysis, we construct a model of set theory in which ${\aleph _2}$-Aronszajn trees exist and all such trees contain ${\aleph _0}$-ascent paths. Finally, we use our techniques to show that the assumption that the κ-Knaster property is countably productive and the assumption that every κ-Knaster partial order is κ-stationarily layered both imply the failure of $\square \left( \kappa \right)$.

We formulate combinatorial principles that combine the square principle with various strong forms of the diamond principle, and prove that the strongest amongst them holds in L for every infinite cardinal.

As an application, we prove that the following two hold in L:

1. 1. For every infinite regular cardinal λ, there exists a special λ+-Aronszajn tree whose projection is almost Souslin;

2. 2. For every infinite cardinal λ, there exists a respecting λ+-Kurepa tree; Roughly speaking, this means that this λ+-Kurepa tree looks very much like the λ+-Souslin trees that Jensen constructed in L.

The history of productivity of the κ-chain condition in partial orders, topological spaces, or Boolean algebras is surveyed, and its connection to the set-theoretic notion of a weakly compact cardinal is highlighted. Then, it is proved that for every regular cardinal 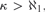$\kappa > \aleph _1 {\rm{,}}$ the principle □(k) is equivalent to the existence of a certain strong coloring 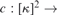$c\,:\,[k]^2 \, \to $k for which the family of fibers 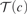${\cal T}\left( c \right)$ is a nonspecial κ-Aronszajn tree.

The theorem follows from an analysis of a new characteristic function for walks on ordinals, and implies in particular that if the κ-chain condition is productive for a given regular cardinal 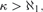$\kappa > \aleph _1 {\rm{,}}$ then κ is weakly compact in some inner model of ZFC. This provides a partial converse to the fact that if κ is a weakly compact cardinal, then the κ-chain condition is productive.