In nonparametric statistics a classical optimality criterion for estimation procedures isprovided by the minimax rate of convergence. However this point of view can be subject tocontroversy as it requires to look for the worst behavior of an estimation procedure in agiven space. The purpose of this paper is to introduce a new criterion based on genericbehavior of estimators. We are here interested in the rate of convergence obtained withsome classical estimators on almost every, in the sense of prevalence, function in a Besovspace. We also show that generic results coincide with minimax ones in these cases.

We present here a new proof of the theorem ofBirman and Solomyak on the metric entropy of the unit ball of aBesov space $B^s_{\pi,q}$ 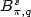on a regular domain of ${\mathbb R}^d.$ 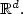Theresult is: if s - d(1/π - 1/p) +> 0, then the Kolmogorov metric entropy satisfies H(ε) ~ ε-d/s . This prooftakes advantage of the representation of such spaces on wavelet typebases and extends the result to more general spaces. The lower boundis a consequence of very simple probabilistic exponentialinequalities. To prove the upper bound, we provide a newuniversal coding based on a thresholding-quantizing procedure usingreplication.