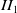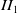1 results
A few remarks on Pimsner–Popa bases and regular subfactors of depth 2
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 01 December 2021, pp. 586-602
- Print publication:
- September 2022
-
- Article
- Export citation
-
We prove that a finite index regular inclusion of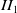
$II_1$
-factors with commutative first relative commutant is always a crossed product subfactor with respect to a minimal action of a biconnected weak Kac algebra. Prior to this, we prove that every finite index inclusion of 
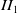$II_1$
-factors which is of depth 2 and has simple first relative commutant (respectively, is regular and has commutative or simple first relative commutant) admits a two-sided Pimsner–Popa basis (respectively, a unitary orthonormal basis).
