We prove a general principle satisfied by weakly precompact sets of Lipschitz-free spaces. By this principle, certain infinite dimensional phenomena in Lipschitz-free spaces over general metric spaces may be reduced to the same phenomena in free spaces over their compact subsets. As easy consequences we derive several new and some known results. The main new results are: $\mathcal {F}(X)$ is weakly sequentially complete for every superreflexive Banach space $X$, and $\mathcal {F}(M)$ has the Schur property and the approximation property for every scattered complete metric space $M$.

For Banach spaces $X$ and $Y$, we show that if ${{X}^{*}}$ and $Y$ are weakly sequentially complete and every weakly compact operator from $X$ to $Y$ is compact, then the space of all compact operators from $X$ to $Y$ is weakly sequentially complete. The converse is also true if, in addition, either ${{X}^{*}}$ or $Y$ has the bounded compact approximation property.

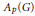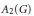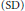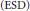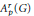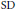Let ${{A}_{p}}\left( G \right)$ be the Figa-Talamanca, Herz Banach Algebra on $G$; thus ${{A}_{2}}\left( G \right)$ is the Fourier algebra. Strong Ditkin $\left( \text{SD} \right)$ and Extremely Strong Ditkin $\left( \text{ESD} \right)$ sets for the Banach algebras $A_{P}^{r}\left( G \right)$ are investigated for abelian and nonabelian locally compact groups $G$. It is shown that $\text{SD}$ and 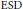$\text{ESD}$ sets for 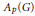${{A}_{p}}\left( G \right)$ remain 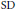$\text{SD}$ and 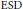$\text{ESD}$ sets for 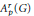$A_{P}^{r}\left( G \right)$, with strict inclusion for 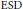$\text{ESD}$ sets. The case for the strict inclusion of 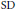$\text{SD}$ sets is left open.

A result on the weak sequential completeness of 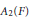${{A}_{2}}\left( F \right)$ for 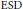$\text{ESD}$ sets $F$ is proved and used to show that Varopoulos, Helson, and Sidon sets are not 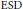$\text{ESD}$ sets for 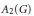${{A}_{2}}\left( G \right)$, yet they are such for 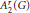$A_{2}^{r}\left( G \right)$ for discrete groups $G$, for any 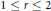$1\,\le \,r\,\le \,2$.

A result is given on the equivalence of the sequential and the net definitions of 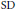$\text{SD}$ or 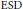$\text{ESD}$ sets for $\sigma $-compact groups.

The above results are new even if $G$ is abelian.