1 results
Matrices Whose Norms Are Determined by Their Actions on Decreasing Sequences
-
- Journal:
- Canadian Journal of Mathematics / Volume 60 / Issue 3 / 01 June 2008
- Published online by Cambridge University Press:
- 20 November 2018, pp. 520-531
- Print publication:
- 01 June 2008
-
- Article
-
- You have access
- Export citation
-
Let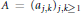
$A={{({{a}_{j,k}})}_{j,k\ge 1}}$ be a non-negative matrix. In this paper, we characterize those 
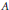$A$ for which 
${{\left\| A \right\|}_{E,F}}$ are determined by their actions on decreasing sequences, where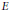 
$E$ and 
$F$ are suitable normed Riesz spaces of sequences. In particular, our results can apply to the following spaces: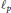 
${{\ell }_{p}}$, 
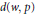$d(w,p)$, and 
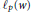${{\ell }_{p}}(w)$. The results established here generalize ones given by Bennett; Chen, Luor, and Ou; Jameson; and Jameson and Lashkaripour.
