In this paper, we study the probability distribution of the word map 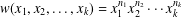$w(x_{1},x_{2},\ldots ,x_{k})=x_{1}^{n_{1}}x_{2}^{n_{2}}\cdots x_{k}^{n_{k}}$ in a compact Lie group. We show that the probability distribution can be represented as an infinite series. Moreover, in the case of the Lie group 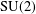$\text{SU}(2)$, our computations give a nice convergent series for the probability distribution.

A finitely generated subgroup ${\rm\Gamma}$ of a real Lie group $G$ is said to be Diophantine if there is ${\it\beta}>0$ such that non-trivial elements in the word ball $B_{{\rm\Gamma}}(n)$ centered at $1\in {\rm\Gamma}$ never approach the identity of $G$ closer than $|B_{{\rm\Gamma}}(n)|^{-{\it\beta}}$. A Lie group $G$ is said to be Diophantine if for every $k\geqslant 1$ a random $k$-tuple in $G$ generates a Diophantine subgroup. Semi-simple Lie groups are conjectured to be Diophantine but very little is proven in this direction. We give a characterization of Diophantine nilpotent Lie groups in terms of the ideal of laws of their Lie algebra. In particular we show that nilpotent Lie groups of class at most $5$, or derived length at most $2$, as well as rational nilpotent Lie groups are Diophantine. We also find that there are non-Diophantine nilpotent and solvable (non-nilpotent) Lie groups.