1 results
Maximizing the probability of visiting a set infinitely often for a Markov decision process with Borel state and action spaces
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 22 August 2024, pp. 1424-1447
- Print publication:
- December 2024
-
- Article
-
- You have access
- HTML
- Export citation
-
We consider a Markov control model with Borel state space, metric compact action space, and transitions assumed to have a density function with respect to some probability measure satisfying some continuity conditions. We study the optimization problem of maximizing the probability of visiting some subset of the state space infinitely often, and we show that there exists an optimal stationary Markov policy for this problem. We endow the set of stationary Markov policies and the family of strategic probability measures with adequate topologies (namely, the narrow topology for Young measures and the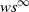
$ws^\infty$-topology, respectively) to obtain compactness and continuity properties, which allow us to obtain our main results.
