No CrossRef data available.
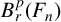 $B^p_r(F_n)$ HAS NO NONTRIVIAL IDEMPOTENTS
$B^p_r(F_n)$ HAS NO NONTRIVIAL IDEMPOTENTSPublished online by Cambridge University Press: 06 October 2022
We show that there is no nontrivial idempotent in the reduced group 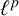 $\ell ^p$-operator algebra
$\ell ^p$-operator algebra 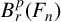 $B^p_r(F_n)$ of the free group
$B^p_r(F_n)$ of the free group 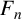 $F_n$ on n generators for each positive integer n.
$F_n$ on n generators for each positive integer n.
The second author is supported by NSFC (No. 12171156).