Published online by Cambridge University Press: 14 September 2023
Multi-cell positron traps have been proposed to accumulate and store large numbers of positrons (e.g. ${\ge }10^{10}$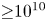 ). This design arranges lines of Penning–Malmberg traps (‘cells’) on and off the magnetic axis in a vacuum chamber in a common, uniform magnetic field. Confinement considerations impose additional constraints on the magnetic field beyond the usual on-axis homogeneity requirements. These requirements are discussed. A prototype magnetic field and associated coil geometry is suggested to achieve good single-component plasma confinement in all cells. Experimental confinement data as a function of electrode alignment with respect to a nominally uniform magnetic field are also presented. These results are related to the field-alignment considerations of the magnet design study.
). This design arranges lines of Penning–Malmberg traps (‘cells’) on and off the magnetic axis in a vacuum chamber in a common, uniform magnetic field. Confinement considerations impose additional constraints on the magnetic field beyond the usual on-axis homogeneity requirements. These requirements are discussed. A prototype magnetic field and associated coil geometry is suggested to achieve good single-component plasma confinement in all cells. Experimental confinement data as a function of electrode alignment with respect to a nominally uniform magnetic field are also presented. These results are related to the field-alignment considerations of the magnet design study.