Published online by Cambridge University Press: 30 November 2023
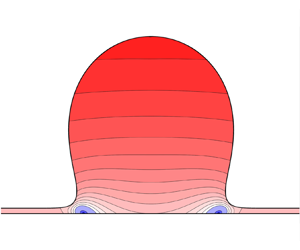
A novel boundary integral approach for the recovery of overhanging (or not) rotational water waves (with constant vorticity) from pressure measurements at the bottom is presented. The method is based on the Cauchy integral formula and on an Eulerian–Lagrangian formalism to accommodate overturning free surfaces. This approach eliminates the need to introduce a priori a special basis of functions, thus providing a general means of fitting the pressure data and, consequently, recovering the free surface. The effectiveness and accuracy of the method are demonstrated through numerical examples.