Published online by Cambridge University Press: 06 December 2023
We generalise the properties  $\mathsf {OP}$,
$\mathsf {OP}$, 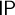 $\mathsf {IP}$, k-
$\mathsf {IP}$, k- $\mathsf {TP}$,
$\mathsf {TP}$,  $\mathsf {TP}_{1}$, k-
$\mathsf {TP}_{1}$, k- $\mathsf {TP}_{2}$,
$\mathsf {TP}_{2}$,  $\mathsf {SOP}_{1}$,
$\mathsf {SOP}_{1}$,  $\mathsf {SOP}_{2}$, and
$\mathsf {SOP}_{2}$, and  $\mathsf {SOP}_{3}$ to positive logic, and prove various implications and equivalences between them. We also provide a characterisation of stability in positive logic in analogy with the one in full first-order logic, both on the level of formulas and on the level of theories. For simple theories there are the classically equivalent definitions of not having
$\mathsf {SOP}_{3}$ to positive logic, and prove various implications and equivalences between them. We also provide a characterisation of stability in positive logic in analogy with the one in full first-order logic, both on the level of formulas and on the level of theories. For simple theories there are the classically equivalent definitions of not having  $\mathsf {TP}$ and dividing having local character, which we prove to be equivalent in positive logic as well. Finally, we show that a thick theory T has
$\mathsf {TP}$ and dividing having local character, which we prove to be equivalent in positive logic as well. Finally, we show that a thick theory T has  $\mathsf {OP}$ iff it has
$\mathsf {OP}$ iff it has 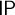 $\mathsf {IP}$ or
$\mathsf {IP}$ or  $\mathsf {SOP}_{1}$ and that T has
$\mathsf {SOP}_{1}$ and that T has  $\mathsf {TP}$ iff it has
$\mathsf {TP}$ iff it has  $\mathsf {SOP}_{1}$ or
$\mathsf {SOP}_{1}$ or  $\mathsf {TP}_{2}$, analogous to the well-known results in full first-order logic where
$\mathsf {TP}_{2}$, analogous to the well-known results in full first-order logic where  $\mathsf {SOP}_{1}$ is replaced by
$\mathsf {SOP}_{1}$ is replaced by 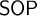 $\mathsf {SOP}$ in the former and by
$\mathsf {SOP}$ in the former and by  $\mathsf {TP}_{1}$ in the latter. Our proofs of these final two theorems are new and make use of Kim-independence.
$\mathsf {TP}_{1}$ in the latter. Our proofs of these final two theorems are new and make use of Kim-independence.