Article contents
Heat transport and flow morphology of geostrophic rotating Rayleigh–Bénard convection in the presence of boundary flow
Published online by Cambridge University Press: 22 November 2023
Abstract
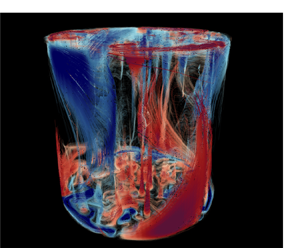
Using direct numerical simulations, we investigate the heat transport in bulk and boundary flows separately in rotating Rayleigh–Bénard convection in cylindrical cells. In the bulk we observe a steep scaling relationship between the Nusselt number ( $Nu$) and the Rayleigh number (
$Nu$) and the Rayleigh number ( $Ra$), which is consistent with the results from simulations using periodic boundary conditions. For the boundary flow, we observe a power law
$Ra$), which is consistent with the results from simulations using periodic boundary conditions. For the boundary flow, we observe a power law  $Nu_{BF}\sim (Ra/Ra_w)^1$ at the leading order, where
$Nu_{BF}\sim (Ra/Ra_w)^1$ at the leading order, where  $Nu_{BF}$ is the local Nusselt number of the boundary flow and
$Nu_{BF}$ is the local Nusselt number of the boundary flow and  $Ra_w$ is the onset Rayleigh number of the wall mode. We develop a model using the boundary layer marginal stability theory to explain this power law, and further show that a more precise description of the data can be obtained if a higher-order correction is introduced. A striking finding of our study is the observation of a sharp transition in flow state, manifested by a sudden drop in
$Ra_w$ is the onset Rayleigh number of the wall mode. We develop a model using the boundary layer marginal stability theory to explain this power law, and further show that a more precise description of the data can be obtained if a higher-order correction is introduced. A striking finding of our study is the observation of a sharp transition in flow state, manifested by a sudden drop in  $Nu_{BF}$ with a corresponding collapse of the boundary flow coherency. After the transition, the boundary flow breaks into vortices, leading to a reduction in flow coherency and heat transport efficiency. As the physical properties of the vortices should not depend on the aspect ratio,
$Nu_{BF}$ with a corresponding collapse of the boundary flow coherency. After the transition, the boundary flow breaks into vortices, leading to a reduction in flow coherency and heat transport efficiency. As the physical properties of the vortices should not depend on the aspect ratio,  $Nu_{BF}$ for all aspect ratios collapse together after the transition. Moreover, the centrifugal force helps trigger the breakdown of the coherent boundary flow state. For this reason,
$Nu_{BF}$ for all aspect ratios collapse together after the transition. Moreover, the centrifugal force helps trigger the breakdown of the coherent boundary flow state. For this reason,  $Nu_{BF}$ for the cases with non-zero centrifugal force collapse together. We further develop a method that enables us to separate the contributions from the bulk and boundary flows in the global Nusselt number using only the global
$Nu_{BF}$ for the cases with non-zero centrifugal force collapse together. We further develop a method that enables us to separate the contributions from the bulk and boundary flows in the global Nusselt number using only the global  $Nu$ and it does not require the centrifugal force to be absent.
$Nu$ and it does not require the centrifugal force to be absent.
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press
References
- 1
- Cited by


