Hostname: page-component-857557d7f7-v48vw Total loading time: 0 Render date: 2025-11-28T23:59:13.025Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE NORMALISERS OF ALL NON-p-NILPOTENT SUBGROUPS IN A FINITE GROUP

Part of: Representation theory of groups

Published online by Cambridge University Press:  28 November 2025

XUAN LI Open the ORCID record for XUAN LI [Opens in a new window] ,
JUNXIN WANG Open the ORCID record for JUNXIN WANG [Opens in a new window]  and
XIUYUN GUO Open the ORCID record for XIUYUN GUO [Opens in a new window]
XUAN LI*
Affiliation:
School of Applied Mathematics, Shanxi University of Finance and Economics , Taiyuan 030006, PR China
JUNXIN WANG
Affiliation:
School of Applied Mathematics, Shanxi University of Finance and Economics , Taiyuan 030006, PR China e-mail: wangjunxin660712@163.com
XIUYUN GUO
Affiliation:
Department of Mathematics, Shanghai University , Shanghai 200444, PR China e-mail: xyguo@staff.shu.edu.cn
*
e-mail: lixuan@sxufe.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

For a prime p, let 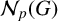$\mathcal {N}_p(G)$ denote the intersection of the normalisers of all non-p-nilpotent subgroups of a finite group G and set $\mathcal {N}_p(G)=G$ if G itself is p-nilpotent. We give some properties of $\mathcal {N}_p(G)$ and investigate the influence of $\mathcal {N}_p(G)$ on G.

Keywords

p-nilpotent subgroupp-solvable groupnormaliser

MSC classification

Primary: 20D10: Solvable groups, theory of formations, Schunck classes, Fitting classes, $pi$-length, ranks
Secondary: 20D20: Sylow subgroups, Sylow properties, $pi$-groups, $pi$-structure

Information

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , First View , pp. 1 - 8
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

The research was partially supported by the National Natural Science Foundation of China (Grant No. 12171302).

References

Baer, R., ‘Der Kern, eine charakteristische Untergruppe’, Compos. Math. 1 (1934), 254–283.Google Scholar
Baer, R., ‘Zentrum und Kern von Gruppen mit Elementen unendlicher Ordnung’, Compos. Math. 2 (1935), 247–249.Google Scholar
Baer, R., ‘Der Kern, Norm and hypernorm’, Publ. Math. Debrecen 4 (1956), 347–350.10.5486/PMD.1956.4.3-4.30CrossRefGoogle Scholar
Ballester-Bolinches, A., Cossey, J. and Zhang, L., ‘Generalised norms in finite soluble groups’, J. Algebra 402 (2014), 392–405.10.1016/j.jalgebra.2013.12.012CrossRefGoogle Scholar
Bruno, B. and Phillips, R. E., ‘Groups with restricted nonnormal subgroups’, Math. Z. 176 (1981), 199–221.10.1007/BF01261869CrossRefGoogle Scholar
Gong, L. and Guo, X., ‘On the intersection of the normalizers of the nilpotent residuals of all subgroups of a finitie group’, Algebra Colloq. 20(2) (2013), 349–360.10.1142/S1005386713000321CrossRefGoogle Scholar
Gorenstein, D., Finite Groups (Chelsea, New York, 1980).Google Scholar
Guo, X. and Wang, J., ‘The power automorphisms and the subgroup lattices in finite groups’, Adv. Math. (China) 2 (2025), 357–378.Google Scholar
Li, S. and Shen, Z., ‘On the intersection of the normalizers of derived subgroups of all subgroups of a finite group’, J. Algebra 323(5) (2010), 1349–1357.10.1016/j.jalgebra.2009.12.015CrossRefGoogle Scholar
Li, X. and Guo, X., ‘On the normalizers of $p$ -nilpotency-residuals of all subgroups in a finite group’, J. Algebra Appl. 14(10) (2015), Article no. 1550146.10.1142/S0219498815501467CrossRefGoogle Scholar
Li, X. and Guo, X., ‘On generalised norms of finite groups’, Comm. Algebra 44(3) (2016), 1088–1095.10.1080/00927872.2014.999927CrossRefGoogle Scholar
Nagrebeckii, V. T., ‘Finite non nilpotent groups, any non abelian subgroup of which is invariant’, Ural. Gos. Univ. Mat. Zap. 6 (1967), 80–88 (in Russian).Google Scholar
Nagrebeckii, V. T., ‘Finite groups in which any nonnilpotent subgroup is invariant’, Ural. Gos. Univ. Mat. Zap. 6 (1968), 45–49 (in Russian).Google Scholar
Robinson, D. J. S., A Course in the Theory of Groups (Springer, New York, 1982).10.1007/978-1-4684-0128-8CrossRefGoogle Scholar
Romalis, G. M. and Sesekin, N. F., ‘Metahamiltonian groups’, Ural. Gos. Univ. Mat. Zap. 5 (1966), 101–106 (in Russian).Google Scholar
Shen, Z., Shi, W. and Qian, G., ‘On the norm of the nilpotent residuals of all subgroups of a finite group’, J. Algebra 352 (2010), 290–298.10.1016/j.jalgebra.2011.11.018CrossRefGoogle Scholar
Shen, Z., Shi, W. and Zhang, J., ‘Finite non-nilpotent generalisations of Hamiltonian groups’, Bull. Korean Math. Soc. 48 (2011), 1147–1155.10.4134/BKMS.2011.48.6.1147CrossRefGoogle Scholar
Su, N. and Wang, Y., ‘On the normalizers of $\mathcal {F}$ -residuals of all subgroups of a finite group’, J. Algebra 392 (2013), 185–198.10.1016/j.jalgebra.2013.06.037CrossRefGoogle Scholar