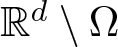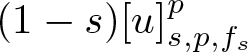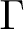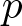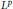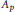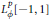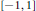Refine search
Actions for selected content:
7 results
On the Γ-limit of weighted fractional energies
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 01 December 2025, pp. 1-22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Existence and uniqueness of solutions to a flow and transport problem with degenerating coefficients
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 03 February 2022, pp. 55-76
-
- Article
-
- You have access
- HTML
- Export citation
Degenerate equations in a diffusion–precipitation model for clogging porous media
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 31 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 18 December 2019, pp. 1050-1069
-
- Article
-
- You have access
- Open access
- Export citation
Transference of Vector-valued Multipliers on Weighted Lp-spaces
-
- Journal:
- Canadian Journal of Mathematics / Volume 65 / Issue 3 / 01 June 2013
- Published online by Cambridge University Press:
- 20 November 2018, pp. 510-543
- Print publication:
- 01 June 2013
-
- Article
-
- You have access
- Export citation
QUASI-MONTE CARLO METHODS FOR HIGH-DIMENSIONAL INTEGRATION: THE STANDARD (WEIGHTED HILBERT SPACE) SETTING AND BEYOND
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 53 / Issue 1 / July 2011
- Published online by Cambridge University Press:
- 29 May 2012, pp. 1-37
-
- Article
-
- You have access
- Export citation
Representation of Banach Ideal Spaces and Factorization of Operators
-
- Journal:
- Canadian Journal of Mathematics / Volume 57 / Issue 5 / 01 October 2005
- Published online by Cambridge University Press:
- 20 November 2018, pp. 897-940
- Print publication:
- 01 October 2005
-
- Article
-
- You have access
- Export citation
Strong Converse Inequalities for Averages in Weighted L p Spaces on [-1,1]
-
- Journal:
- Canadian Journal of Mathematics / Volume 51 / Issue 3 / 01 June 1999
- Published online by Cambridge University Press:
- 20 November 2018, pp. 546-565
- Print publication:
- 01 June 1999
-
- Article
-
- You have access
- Export citation