No CrossRef data available.
Published online by Cambridge University Press: 17 February 2009
Let Δ denote a triangulation of a planar polygon Ω. For any positive integer 0 ≤ r < k, let 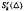 denote the vector space of functions in Cr whose restrictions to each triangle of Δ are polynomials of total degree at most k. Such spaces, called bivariate spline spaces, have many applications in surface fitting, scattered data interpolation, function approximation and numerical solutions of partial differential equations. An important problem is to give the function expression. In this paper, we prove that, if (Δ, Ω) is type-X, then any bivariate spline function in
denote the vector space of functions in Cr whose restrictions to each triangle of Δ are polynomials of total degree at most k. Such spaces, called bivariate spline spaces, have many applications in surface fitting, scattered data interpolation, function approximation and numerical solutions of partial differential equations. An important problem is to give the function expression. In this paper, we prove that, if (Δ, Ω) is type-X, then any bivariate spline function in 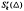 can be expressed by a series of univariate polynomials and a special bivariate finite element function in
can be expressed by a series of univariate polynomials and a special bivariate finite element function in 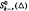 satisfying a so-called integral conformality condition system. We also give a direct sum decomposition of the space
satisfying a so-called integral conformality condition system. We also give a direct sum decomposition of the space 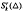 . In addition, the dimension of
. In addition, the dimension of 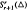 for a kind of triangulation has been determined.
for a kind of triangulation has been determined.