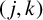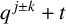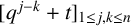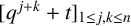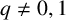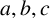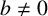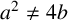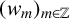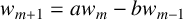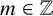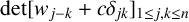1. Introduction
For any integer
![]() $n\ge 3$
, we have the determinant identity
$n\ge 3$
, we have the determinant identity
since
![]() $(1-k)+(3-k)=2(2-k)$
for all
$(1-k)+(3-k)=2(2-k)$
for all
![]() $k=1,\ldots ,n$
. However, it is nontrivial to deter- mine the characteristic polynomial
$k=1,\ldots ,n$
. However, it is nontrivial to deter- mine the characteristic polynomial
![]() $\det [xI_n-(\,j-k)]_{1\le \,j,k\le n}$
of the matrix
$\det [xI_n-(\,j-k)]_{1\le \,j,k\le n}$
of the matrix
![]() $[\,j-k]_{1\le \,j,k\le n}$
, where
$[\,j-k]_{1\le \,j,k\le n}$
, where
![]() $I_n$
is the identity matrix of order n.
$I_n$
is the identity matrix of order n.
For
![]() $j,k\in \mathbb N=\{0,1,2,\ldots \}$
, the Kronecker symbol
$j,k\in \mathbb N=\{0,1,2,\ldots \}$
, the Kronecker symbol
![]() $\delta _{jk}$
takes the value
$\delta _{jk}$
takes the value
![]() $1$
or
$1$
or
![]() $0$
according to whether
$0$
according to whether
![]() $j=k$
or not. In 2003, Cloitre [Reference Cloitre1] generated the sequence
$j=k$
or not. In 2003, Cloitre [Reference Cloitre1] generated the sequence
![]() $\det [\,j-k+\delta _{jk}]_{1\le \,j,k\le n}$
$\det [\,j-k+\delta _{jk}]_{1\le \,j,k\le n}$
![]() $(n=1,2,3,\ldots )$
with the initial fifteen terms:
$(n=1,2,3,\ldots )$
with the initial fifteen terms:
In 2013, C. Baker added a comment to [Reference Cloitre1] in which he claimed that
without any proof. It seems that Baker found the recurrence of the sequence using the Maple package gfun.
Recall that the q-analogue of an integer m is given by
 $$ \begin{align*}[m]_q=\frac{q^m-1}{q-1}.\end{align*} $$
$$ \begin{align*}[m]_q=\frac{q^m-1}{q-1}.\end{align*} $$
Note that
![]() $\lim _{q\to 1}[m]_q=m$
.
$\lim _{q\to 1}[m]_q=m$
.
In our first theorem, we determine the characteristic polynomial of the matrix
![]() $[q^{\,j-k}+t]_{1\le \,j,k\le n}$
for any complex number
$[q^{\,j-k}+t]_{1\le \,j,k\le n}$
for any complex number
![]() $q\not =0,1$
.
$q\not =0,1$
.
Theorem 1.1. Let
![]() $n\ge 2$
be an integer and let
$n\ge 2$
be an integer and let
![]() $q\not =0,1$
be a complex number. Then the characteristic polynomial of the matrix
$q\not =0,1$
be a complex number. Then the characteristic polynomial of the matrix
![]() $P=[q^{\,j-k}+t]_{1\le \,j,k\le n}$
is
$P=[q^{\,j-k}+t]_{1\le \,j,k\le n}$
is
Putting
![]() $t=-1$
and replacing x by
$t=-1$
and replacing x by
![]() $(q-1)x$
in Theorem 1.1, we immediately obtain the following corollary.
$(q-1)x$
in Theorem 1.1, we immediately obtain the following corollary.
Corollary 1.2. Let
![]() $n\ge 2$
be an integer and let
$n\ge 2$
be an integer and let
![]() $q\not =0,1$
be a complex number. For the matrix
$q\not =0,1$
be a complex number. For the matrix
![]() $P_q=[[\,j-k]_q]_{1\le \,j,k\le n}$
,
$P_q=[[\,j-k]_q]_{1\le \,j,k\le n}$
,
 $$ \begin{align*}\det(xI_n-P_q)=x^{n}+\frac{q^{1-n}[n]_q^2-n^2}{(q-1)^2}x^{n-2}. \end{align*} $$
$$ \begin{align*}\det(xI_n-P_q)=x^{n}+\frac{q^{1-n}[n]_q^2-n^2}{(q-1)^2}x^{n-2}. \end{align*} $$
Remark 1.3. Fix an integer
![]() $n\ge 2$
. Observe that
$n\ge 2$
. Observe that
 $$ \begin{align*}\lim_{q\to1}\frac{q^{1-n}[n]_q^2-n^2}{(q-1)^2} &=\lim_{t\to0}\frac{(t+1)^{1-n}(((t+1)^n-1)/t)^2-n^2}{t^2} \\&=\lim_{t\to0}\frac{(t+1)^{1-n}((\sum_{k=1}^n\binom nkt^{k-1})^2-n^2)+((t+1)^{1-n}-1)n^2}{t^2} \\&=\lim_{t\to0}\bigg(\frac{(n+\binom n2t+\binom n3t^2+\cdots)^2-n^2}{(t+1)^{n-1}t^2}+n^2\frac{1-(t+1)^{n-1}}{(t+1)^{n-1}t^2}\bigg) \\&=\binom n2^2+2n\binom n3+\lim_{t\to0}\bigg(2n\binom n2\frac{t^{-1}}{(t+1)^{n-1}}-n^2\frac{\sum_{k=1}^n\binom{n-1}kt^{k-2}}{(t+1)^{n-1}}\bigg) \\&=\binom n2^2+2n\binom n3-n^2\binom{n-1}2 =\frac{n^2(n^2-1)}{12}. \end{align*} $$
$$ \begin{align*}\lim_{q\to1}\frac{q^{1-n}[n]_q^2-n^2}{(q-1)^2} &=\lim_{t\to0}\frac{(t+1)^{1-n}(((t+1)^n-1)/t)^2-n^2}{t^2} \\&=\lim_{t\to0}\frac{(t+1)^{1-n}((\sum_{k=1}^n\binom nkt^{k-1})^2-n^2)+((t+1)^{1-n}-1)n^2}{t^2} \\&=\lim_{t\to0}\bigg(\frac{(n+\binom n2t+\binom n3t^2+\cdots)^2-n^2}{(t+1)^{n-1}t^2}+n^2\frac{1-(t+1)^{n-1}}{(t+1)^{n-1}t^2}\bigg) \\&=\binom n2^2+2n\binom n3+\lim_{t\to0}\bigg(2n\binom n2\frac{t^{-1}}{(t+1)^{n-1}}-n^2\frac{\sum_{k=1}^n\binom{n-1}kt^{k-2}}{(t+1)^{n-1}}\bigg) \\&=\binom n2^2+2n\binom n3-n^2\binom{n-1}2 =\frac{n^2(n^2-1)}{12}. \end{align*} $$
So, by Corollary 1.2,
which indicates that when
![]() $n>2$
, the n eigenvalues of
$n>2$
, the n eigenvalues of
![]() $A_n=[\,j-k]_{1\le \,j,k\le n}$
are
$A_n=[\,j-k]_{1\le \,j,k\le n}$
are
 $$ \begin{align*}\lambda_1=\frac{n\sqrt{n^2-1}}{2\sqrt3}\,i,\quad \lambda_2=-\frac{n\sqrt{n^2-1}}{2\sqrt3}\,i,\quad \lambda_3=\cdots=\lambda_n=0.\end{align*} $$
$$ \begin{align*}\lambda_1=\frac{n\sqrt{n^2-1}}{2\sqrt3}\,i,\quad \lambda_2=-\frac{n\sqrt{n^2-1}}{2\sqrt3}\,i,\quad \lambda_3=\cdots=\lambda_n=0.\end{align*} $$
Note that (1.1) follows from (1.3) with
![]() $x=-1$
. Concerning the permanent of
$x=-1$
. Concerning the permanent of
![]() $A_n$
, motivated by [Reference Sun3, Conjecture 11.23], we conjecture that
$A_n$
, motivated by [Reference Sun3, Conjecture 11.23], we conjecture that
for any odd prime p. Inspired by (1.1), Sun [Reference Sun4] conjectured that for any positive integers m and n,
for a certain polynomial
![]() $f(x)\in \mathbb Q[x]$
with
$f(x)\in \mathbb Q[x]$
with
![]() $\deg f=(m+1)^2-4$
.
$\deg f=(m+1)^2-4$
.
Applying Corollary 1.2 with
![]() $q=-1$
, we find that
$q=-1$
, we find that
 $$ \begin{align*}\det(xI_n-P_{-1})=x^n+\frac{(-1)^{n-1}[n]_{-1}^2-n^2}4x^{n-2}\end{align*} $$
$$ \begin{align*}\det(xI_n-P_{-1})=x^n+\frac{(-1)^{n-1}[n]_{-1}^2-n^2}4x^{n-2}\end{align*} $$
for any integer
![]() $n\ge 2$
. In particular,
$n\ge 2$
. In particular,
 $$ \begin{align*}\det\bigg[\frac{1-(-1)^{\,j-k}}2+\delta_{\,j,k}\bigg]_{1\le \,j,k\le n}=\frac{9-(-1)^n-2n^2}8.\end{align*} $$
$$ \begin{align*}\det\bigg[\frac{1-(-1)^{\,j-k}}2+\delta_{\,j,k}\bigg]_{1\le \,j,k\le n}=\frac{9-(-1)^n-2n^2}8.\end{align*} $$
Applying Theorem 1.1 with
![]() $(t,x)=(-1,-2)$
and
$(t,x)=(-1,-2)$
and
![]() $(1,-1)$
, we obtain the following result.
$(1,-1)$
, we obtain the following result.
Corollary 1.4. For any positive integer n,
and
In contrast to Theorem 1.1, we also establish the following result.
Theorem 1.5. Let
![]() $n\ge 2$
be an integer and let
$n\ge 2$
be an integer and let
![]() $q\not =0,1$
be a complex number. Then the characteristic polynomial of the matrix
$q\not =0,1$
be a complex number. Then the characteristic polynomial of the matrix
![]() $Q=[q^{\,j+k}+t]_{0\le \,j,k\le n-1}$
is
$Q=[q^{\,j+k}+t]_{0\le \,j,k\le n-1}$
is
The identity (1.4) with
![]() $q=2$
and
$q=2$
and
![]() $x=t=-1$
yields the following corollary.
$x=t=-1$
yields the following corollary.
Corollary 1.6. For any positive integer n,
For complex numbers a and
![]() $b\not =0$
, the Lucas sequence
$b\not =0$
, the Lucas sequence
![]() $u_m=u_m(a,b)$
$u_m=u_m(a,b)$
![]() $(m\in \mathbb Z)$
and its companion sequence
$(m\in \mathbb Z)$
and its companion sequence
![]() $v_m=v_m(a,b)$
$v_m=v_m(a,b)$
![]() $(m\in \mathbb Z)$
are defined as follows:
$(m\in \mathbb Z)$
are defined as follows:
 $$ \begin{gather*}u_0=0,\ u_1=1\quad \text{and} \quad u_{k+1}=au_k-bu_{k-1}\quad \text{for all } k\in\mathbb Z; \\v_0=2,\ v_1=a\quad \text{and} \quad v_{k+1}=av_k-bv_{k-1}\quad \text{for all } k\in\mathbb Z. \end{gather*} $$
$$ \begin{gather*}u_0=0,\ u_1=1\quad \text{and} \quad u_{k+1}=au_k-bu_{k-1}\quad \text{for all } k\in\mathbb Z; \\v_0=2,\ v_1=a\quad \text{and} \quad v_{k+1}=av_k-bv_{k-1}\quad \text{for all } k\in\mathbb Z. \end{gather*} $$
By the Binet formula,
where
 $$ \begin{align}\alpha=\frac{a+\sqrt{a^2-4b}}2\quad \text{and}\quad \beta=\frac{a-\sqrt{a^2-4b}}2\end{align} $$
$$ \begin{align}\alpha=\frac{a+\sqrt{a^2-4b}}2\quad \text{and}\quad \beta=\frac{a-\sqrt{a^2-4b}}2\end{align} $$
are the two roots of the quadratic equation
![]() $x^2-ax+b=0$
. Clearly,
$x^2-ax+b=0$
. Clearly,
![]() $b^nu_{-n}=-u_n$
and
$b^nu_{-n}=-u_n$
and
![]() $b^nv_{-n}=v_n$
for all
$b^nv_{-n}=v_n$
for all
![]() $n\in \mathbb N$
. For any positive integer n, it is known that
$n\in \mathbb N$
. For any positive integer n, it is known that
 $$ \begin{align*}u_n=\sum_{k=0}^{\lfloor(n-1)/2\rfloor}\binom{n-1-k}ka^{n-1-2k}(-b)^k \quad \text{and}\quad v_n=\sum_{k=0}^{\lfloor n/2\rfloor}\frac n{n-k}\binom{n-k}ka^{n-2k}(-b)^k\end{align*} $$
$$ \begin{align*}u_n=\sum_{k=0}^{\lfloor(n-1)/2\rfloor}\binom{n-1-k}ka^{n-1-2k}(-b)^k \quad \text{and}\quad v_n=\sum_{k=0}^{\lfloor n/2\rfloor}\frac n{n-k}\binom{n-k}ka^{n-2k}(-b)^k\end{align*} $$
(see [Reference Sun5, page 10]), which can be easily proved by induction. Note also that
![]() $u_m(2,1)=m$
for all
$u_m(2,1)=m$
for all
![]() $m\in \mathbb Z$
.
$m\in \mathbb Z$
.
For
![]() $P(z)=\sum _{k=0}^{n-1}a_kz^k\in \mathbb C[z]$
, it is known (see [Reference Krattenthaler2, Lemma 9]) that
$P(z)=\sum _{k=0}^{n-1}a_kz^k\in \mathbb C[z]$
, it is known (see [Reference Krattenthaler2, Lemma 9]) that
 $$ \begin{align*}\det[P(x_{\,j}+y_k)]_{1\le \,j,k\le n}=a_{n-1}^n\prod_{r=0}^{n-1}\binom{n-1}r\times\prod_{1\le \,j<k\le n}(x_j-x_k)(y_k-y_j).\end{align*} $$
$$ \begin{align*}\det[P(x_{\,j}+y_k)]_{1\le \,j,k\le n}=a_{n-1}^n\prod_{r=0}^{n-1}\binom{n-1}r\times\prod_{1\le \,j<k\le n}(x_j-x_k)(y_k-y_j).\end{align*} $$
Thus, for any integer
![]() $n\ge 3$
and complex numbers a and
$n\ge 3$
and complex numbers a and
![]() $b\not =0$
,
$b\not =0$
,
(where
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
are given by (1.5)), since
$\beta $
are given by (1.5)), since
 $$ \begin{align*}\det[\alpha^{\,j-k}\pm\beta^{\,j-k}]_{1\le \,j,k\le n} =\prod_{k=1}^n\alpha^{-k}\times\prod_{\,j=1}^n\beta^{\,j}\times\det\bigg[\bigg(\frac{\alpha}{\beta}\bigg)^{\,j} \pm\bigg(\frac{\alpha}{\beta}\bigg)^k\bigg]_{1\le \,j,k\le n}=0. \end{align*} $$
$$ \begin{align*}\det[\alpha^{\,j-k}\pm\beta^{\,j-k}]_{1\le \,j,k\le n} =\prod_{k=1}^n\alpha^{-k}\times\prod_{\,j=1}^n\beta^{\,j}\times\det\bigg[\bigg(\frac{\alpha}{\beta}\bigg)^{\,j} \pm\bigg(\frac{\alpha}{\beta}\bigg)^k\bigg]_{1\le \,j,k\le n}=0. \end{align*} $$
As an application of Theorem 1.1, we obtain the following new result.
Theorem 1.7. Let a and
![]() $b\not =0$
be complex numbers with
$b\not =0$
be complex numbers with
![]() $a^2\not =4b$
. Let
$a^2\not =4b$
. Let
![]() $(w_m)_{m\in \mathbb Z}$
be a sequence of complex numbers with
$(w_m)_{m\in \mathbb Z}$
be a sequence of complex numbers with
![]() $w_{k+1}=aw_k-bw_{k-1}$
for all
$w_{k+1}=aw_k-bw_{k-1}$
for all
![]() $k\in \mathbb Z$
. For any complex number c and integer
$k\in \mathbb Z$
. For any complex number c and integer
![]() $n\ge 2$
,
$n\ge 2$
,
 $$ \begin{align}\det[w_{\,j-k}+c\delta_{jk}]_{1\le \,j,k\le n} =c^n+c^{n-1}nw_0+c^{n-2}(w_1^2-aw_0w_1+bw_0^2)\frac{b^{1-n}u_n(a,b)^2-n^2}{a^2-4b}. \end{align} $$
$$ \begin{align}\det[w_{\,j-k}+c\delta_{jk}]_{1\le \,j,k\le n} =c^n+c^{n-1}nw_0+c^{n-2}(w_1^2-aw_0w_1+bw_0^2)\frac{b^{1-n}u_n(a,b)^2-n^2}{a^2-4b}. \end{align} $$
Remark 1.8. It would be hard to guess the exact formula for
![]() $\det [w_{\,j-k}+c\delta _{jk}]_{1\le \,j,k\le n}$
in Theorem 1.7 by looking at various numerical examples.
$\det [w_{\,j-k}+c\delta _{jk}]_{1\le \,j,k\le n}$
in Theorem 1.7 by looking at various numerical examples.
Corollary 1.9. Let
![]() $a,b,c$
be complex numbers with
$a,b,c$
be complex numbers with
![]() $b\not =0$
and
$b\not =0$
and
![]() $a^2\not =4b$
. For any integer
$a^2\not =4b$
. For any integer
![]() $n\ge 2$
,
$n\ge 2$
,
 $$ \begin{align*} \det[u_{\,j-k}(a,b)+c\delta_{jk}]_{1\le \,j,k\le n}=c^n+c^{n-2}\frac{b^{1-n}u_n(a,b)^2-n^2}{a^2-4b} \end{align*} $$
$$ \begin{align*} \det[u_{\,j-k}(a,b)+c\delta_{jk}]_{1\le \,j,k\le n}=c^n+c^{n-2}\frac{b^{1-n}u_n(a,b)^2-n^2}{a^2-4b} \end{align*} $$
and
For any
![]() $m\in \mathbb Z$
,
$m\in \mathbb Z$
,
![]() $u_m(-1,1)$
coincides with the Legendre symbol
$u_m(-1,1)$
coincides with the Legendre symbol
![]() $(\frac {m}{3})$
, and
$(\frac {m}{3})$
, and
![]() $v_m(1,-1)=\omega ^m+\bar \omega ^m$
, where
$v_m(1,-1)=\omega ^m+\bar \omega ^m$
, where
![]() $\omega $
denotes the cube root
$\omega $
denotes the cube root
![]() $(-1+\sqrt {-3})/2$
of unity. Applying Corollary 1.9 with
$(-1+\sqrt {-3})/2$
of unity. Applying Corollary 1.9 with
![]() $a=-1$
and
$a=-1$
and
![]() $b=1$
, we get the following result.
$b=1$
, we get the following result.
Corollary 1.10. For any integer
![]() $n\ge 2$
and complex number c,
$n\ge 2$
and complex number c,
 $$ \begin{align*} \det\bigg[\bigg(\frac{\,j-k}3\bigg)+c\delta_{\,j,k}\bigg]_{1\le \,j,k\le n}=c^n+c^{n-2}\bigg\lfloor\frac{n^2}3\bigg\rfloor. \end{align*} $$
$$ \begin{align*} \det\bigg[\bigg(\frac{\,j-k}3\bigg)+c\delta_{\,j,k}\bigg]_{1\le \,j,k\le n}=c^n+c^{n-2}\bigg\lfloor\frac{n^2}3\bigg\rfloor. \end{align*} $$
Recall that
![]() $F_m=u_m(1,-1)$
(
$F_m=u_m(1,-1)$
(
![]() $m\in \mathbb Z$
) are the well-known Fibonacci numbers and
$m\in \mathbb Z$
) are the well-known Fibonacci numbers and
![]() $L_m=v_m(1,-1)$
$L_m=v_m(1,-1)$
![]() $(m\in \mathbb Z$
) are the Lucas numbers. Corollary 1.9 with
$(m\in \mathbb Z$
) are the Lucas numbers. Corollary 1.9 with
![]() $a=1$
and
$a=1$
and
![]() $b=-1$
yields the following result.
$b=-1$
yields the following result.
Corollary 1.11. For any integer
![]() $n\ge 2$
and complex number c,
$n\ge 2$
and complex number c,
and
Although we have Theorem 1.5 which is similar to Theorem 1.1, it seems impossible to use Theorem 1.5 to deduce a result similar to Theorem 1.7.
2. Proof of Theorem 1.1
Lemma 2.1. Let n be a positive integer, and let
![]() $q\neq 0$
and t be complex numbers with
$q\neq 0$
and t be complex numbers with
![]() $n-[n]_q+t(q^{1-n}[n]_q-n)\not =0$
. Suppose that
$n-[n]_q+t(q^{1-n}[n]_q-n)\not =0$
. Suppose that
 $$ \begin{align} \gamma=\frac{n(t+1)\pm\sqrt{n^2(t-1)^2+4tq^{1-n}[n]_q^2}}2 \quad \text{and}\quad y=\frac{\gamma-[n]_q-nt}{n-[n]_q+(q^{1-n}[n]_q-n)t}. \end{align} $$
$$ \begin{align} \gamma=\frac{n(t+1)\pm\sqrt{n^2(t-1)^2+4tq^{1-n}[n]_q^2}}2 \quad \text{and}\quad y=\frac{\gamma-[n]_q-nt}{n-[n]_q+(q^{1-n}[n]_q-n)t}. \end{align} $$
Then, for any positive integer j,
 $$ \begin{align} \sum_{k=1}^n(q^{\,j-k}+t)(1+y(q^{k-n}-1))=\gamma(1+y(q^{\,j-n}-1)). \end{align} $$
$$ \begin{align} \sum_{k=1}^n(q^{\,j-k}+t)(1+y(q^{k-n}-1))=\gamma(1+y(q^{\,j-n}-1)). \end{align} $$
Proof. As
![]() $\gamma ^2-n(t+1)\gamma +(n^2-q^{1-n}[n]_q^2)t=0,$
$\gamma ^2-n(t+1)\gamma +(n^2-q^{1-n}[n]_q^2)t=0,$
and hence
For
![]() $j\in \{1,2,3,\ldots \}$
, set
$j\in \{1,2,3,\ldots \}$
, set
 $$ \begin{align*}\Delta_{\,j}=\sum_{k=1}^n(q^{\,j-k}+t)(1+y(q^{k-n}-1))-\gamma(1+y(q^{\,j-n}-1)).\end{align*} $$
$$ \begin{align*}\Delta_{\,j}=\sum_{k=1}^n(q^{\,j-k}+t)(1+y(q^{k-n}-1))-\gamma(1+y(q^{\,j-n}-1)).\end{align*} $$
Then, by (2.3),
 $$ \begin{align*} \Delta_{\,j}-t(1+y(q^{k-n}-1))+\gamma(1-y) & = q^{\,j-n}\bigg(\sum_{k=1}^nq^{n-k}(1+y(q^{k-n}-1))-\gamma y\bigg) \\ & =q^{\,j-n}([n]_q(1-y)+ny-\gamma y)=0. \end{align*} $$
$$ \begin{align*} \Delta_{\,j}-t(1+y(q^{k-n}-1))+\gamma(1-y) & = q^{\,j-n}\bigg(\sum_{k=1}^nq^{n-k}(1+y(q^{k-n}-1))-\gamma y\bigg) \\ & =q^{\,j-n}([n]_q(1-y)+ny-\gamma y)=0. \end{align*} $$
So
![]() $\Delta _1=\Delta _2=\cdots $
.
$\Delta _1=\Delta _2=\cdots $
.
Next we show that
![]() $\Delta _n=0$
. Observe that
$\Delta _n=0$
. Observe that
 $$ \begin{align*} \sum_{k=1}^n(q^{n-k}+t)(1+(q^{k-n}-1)y) & =\sum_{k=1}^n(q^{n-k}(1-y)+t(1-y)+y+q^{k-n}ty) \\ & = [n]_q(1-y)+nt(1-y)+ny+q^{1-n}[n]_qty \\ & = [n]_q+nt+y(n-[n]_q+(q^{1-n}[n]_q-n)t) \\ & = \gamma=\gamma(1+y(q^{n-n}-1)) \end{align*} $$
$$ \begin{align*} \sum_{k=1}^n(q^{n-k}+t)(1+(q^{k-n}-1)y) & =\sum_{k=1}^n(q^{n-k}(1-y)+t(1-y)+y+q^{k-n}ty) \\ & = [n]_q(1-y)+nt(1-y)+ny+q^{1-n}[n]_qty \\ & = [n]_q+nt+y(n-[n]_q+(q^{1-n}[n]_q-n)t) \\ & = \gamma=\gamma(1+y(q^{n-n}-1)) \end{align*} $$
by the definition of y. So
![]() $\Delta _n=0$
.
$\Delta _n=0$
.
In view of the above,
![]() $\Delta _{j}=0$
for all
$\Delta _{j}=0$
for all
![]() $j=1,2,3,\ldots $
. This concludes the proof.
$j=1,2,3,\ldots $
. This concludes the proof.
Proof of Theorem 1.1.
It is easy to verify the desired result for
![]() $n=2$
. Below we assume that
$n=2$
. Below we assume that
![]() $n\ge 3$
.
$n\ge 3$
.
If
![]() $n-[n]_q$
and
$n-[n]_q$
and
![]() $q^{1-n}[n]_q-n$
are both zero, then
$q^{1-n}[n]_q-n$
are both zero, then
![]() $q^{n-1}=1$
and
$q^{n-1}=1$
and
![]() $n=[n]_q=1$
. As
$n=[n]_q=1$
. As
![]() $n\ge 3$
, there are infinitely many
$n\ge 3$
, there are infinitely many
![]() $t\in \mathbb C$
such that
$t\in \mathbb C$
such that
Take such a number t, and choose
![]() $\gamma $
and y as in (2.1). Then
$\gamma $
and y as in (2.1). Then
![]() $\gamma $
given in (2.1) is an eigenvalue of the matrix
$\gamma $
given in (2.1) is an eigenvalue of the matrix
![]() $P=[q^{\,j-k}+t]_{1\le \,j,k\le n}$
, and the column vector
$P=[q^{\,j-k}+t]_{1\le \,j,k\le n}$
, and the column vector
![]() $v=(v_1,\ldots ,v_n)^T$
with
$v=(v_1,\ldots ,v_n)^T$
with
![]() $v_k=1+y(q^{k-n}-1)$
is an eigenvector of P associated with the eigenvalue
$v_k=1+y(q^{k-n}-1)$
is an eigenvector of P associated with the eigenvalue
![]() $\gamma $
. Note that
$\gamma $
. Note that
![]() $\gamma $
given by (2.1) has two different choices since
$\gamma $
given by (2.1) has two different choices since
![]() $n^2(t-1)^2+4tq^{1-n}[n]_q^2\not =0$
.
$n^2(t-1)^2+4tq^{1-n}[n]_q^2\not =0$
.
Let
![]() $s\in \{3,\ldots ,n\}$
. For
$s\in \{3,\ldots ,n\}$
. For
![]() $1\le k\le n$
, let us define
$1\le k\le n$
, let us define
 $$ \begin{align*}v^{(s)}_k= \begin{cases} q^{2-s}[s-2]_q&\text{if}\ k=1, \\ -q^{2-s}[s-1]_q&\text{if}\ k=2, \\ \delta_{sk}&\text{if}\ 3\le k\le n. \end{cases}\end{align*} $$
$$ \begin{align*}v^{(s)}_k= \begin{cases} q^{2-s}[s-2]_q&\text{if}\ k=1, \\ -q^{2-s}[s-1]_q&\text{if}\ k=2, \\ \delta_{sk}&\text{if}\ 3\le k\le n. \end{cases}\end{align*} $$
It is easy to verify that
 $$ \begin{align*}\sum_{k=1}^nv^{(s)}_k=0=\sum_{k=1}^nq^{\,j-k}v^{(s)}_k\quad \text{for all}\ j=1,\ldots,n.\end{align*} $$
$$ \begin{align*}\sum_{k=1}^nv^{(s)}_k=0=\sum_{k=1}^nq^{\,j-k}v^{(s)}_k\quad \text{for all}\ j=1,\ldots,n.\end{align*} $$
Thus,
![]() $0$
is an eigenvalue of the matrix
$0$
is an eigenvalue of the matrix
![]() $P=[q^{\,j-k}+t]_{1\le \,j,k\le n}$
, and the column vector
$P=[q^{\,j-k}+t]_{1\le \,j,k\le n}$
, and the column vector
![]() $v^{(s)}=(v^{(s)}_1,\ldots ,v^{(s)}_n)^T$
is an eigenvector of P associated with the eigenvalue
$v^{(s)}=(v^{(s)}_1,\ldots ,v^{(s)}_n)^T$
is an eigenvector of P associated with the eigenvalue
![]() $0$
.
$0$
.
If
![]() $\sum _{s=3}^n c_sv^{(s)}$
is the zero column vector for some
$\sum _{s=3}^n c_sv^{(s)}$
is the zero column vector for some
![]() $c_3,\ldots ,c_n\in \mathbb C$
, then for each
$c_3,\ldots ,c_n\in \mathbb C$
, then for each
![]() $k=3,\ldots ,n$
,
$k=3,\ldots ,n$
,
 $$ \begin{align*}c_k=\sum_{s=3}^n c_s\delta_{sk}=\sum_{s=3}^n c_sv^{(s)}_k=0.\end{align*} $$
$$ \begin{align*}c_k=\sum_{s=3}^n c_s\delta_{sk}=\sum_{s=3}^n c_sv^{(s)}_k=0.\end{align*} $$
Thus, the
![]() $n-2$
column vectors
$n-2$
column vectors
![]() $v^{(3)},\ldots ,v^{(n)}$
are linearly independent over
$v^{(3)},\ldots ,v^{(n)}$
are linearly independent over
![]() $\mathbb C$
.
$\mathbb C$
.
By the above, the n eigenvalues of the matrix
![]() $P=[q^{\,j-k}+t]_{1\le \,j,k\le n}$
are the two values of
$P=[q^{\,j-k}+t]_{1\le \,j,k\le n}$
are the two values of
![]() $\gamma $
given by (2.2) and
$\gamma $
given by (2.2) and
![]() $\lambda _3=\cdots =\lambda _n=0$
. Thus, the characteristic polynomial of P is
$\lambda _3=\cdots =\lambda _n=0$
. Thus, the characteristic polynomial of P is
 $$ \begin{align*}\det(xI_n-P)&=\bigg(x-\frac{n(t+1)}2-\frac{\sqrt{n^2(t-1)^2+4tq^{1-n}[n]_q^2}}2\bigg) \\&\quad\times\bigg(x-\frac{n(t+1)}2+\frac{\sqrt{n^2(t-1)^2+4tq^{1-n}[n]_q^2}}2\bigg)\prod_{s=3}^n(x-\lambda_s) \\&=x^{n-2}\bigg(\bigg(x-\frac{n(t+1)}2\bigg)^2-\frac{n^2(t-1)^2+4tq^{1-n}[n]_q^2}4\bigg) \\&=x^{n-2}(x^2-n(t+1)x+t(n^2-q^{1-n}[n]_q^2)). \end{align*} $$
$$ \begin{align*}\det(xI_n-P)&=\bigg(x-\frac{n(t+1)}2-\frac{\sqrt{n^2(t-1)^2+4tq^{1-n}[n]_q^2}}2\bigg) \\&\quad\times\bigg(x-\frac{n(t+1)}2+\frac{\sqrt{n^2(t-1)^2+4tq^{1-n}[n]_q^2}}2\bigg)\prod_{s=3}^n(x-\lambda_s) \\&=x^{n-2}\bigg(\bigg(x-\frac{n(t+1)}2\bigg)^2-\frac{n^2(t-1)^2+4tq^{1-n}[n]_q^2}4\bigg) \\&=x^{n-2}(x^2-n(t+1)x+t(n^2-q^{1-n}[n]_q^2)). \end{align*} $$
Thus, the identity (1.2) holds for infinitely many values of t. Note that both sides of (1.2) are polynomials in t for any fixed
![]() $x\in \mathbb C$
. Thus, if we view both sides of (1.2) as polynomials in x and t, then the identity (1.2) still holds. This completes the proof.
$x\in \mathbb C$
. Thus, if we view both sides of (1.2) as polynomials in x and t, then the identity (1.2) still holds. This completes the proof.
3. Proof of Theorem 1.5
The following lemma is quite similar to Lemma 2.1.
Lemma 3.1. Let n be a positive integer, and let
![]() $q\neq 0$
and t be complex numbers with
$q\neq 0$
and t be complex numbers with
![]() $[n]_{q^2}+(q^{1-n}t-q^{n-1})[n]_q-nt\neq 0$
. Suppose that
$[n]_{q^2}+(q^{1-n}t-q^{n-1})[n]_q-nt\neq 0$
. Suppose that
 $$ \begin{align} \gamma=\frac{nt+[n]_{q^2}\pm\sqrt{(nt-[n]_{q^2})^2+4t[n]_q^2}}2 \quad \text{and}\quad z=\frac{\gamma-q^{n-1}[n]_q-nt}{[n]_{q^2}+(q^{1-n}t-q^{n-1})[n]_q-nt}. \end{align} $$
$$ \begin{align} \gamma=\frac{nt+[n]_{q^2}\pm\sqrt{(nt-[n]_{q^2})^2+4t[n]_q^2}}2 \quad \text{and}\quad z=\frac{\gamma-q^{n-1}[n]_q-nt}{[n]_{q^2}+(q^{1-n}t-q^{n-1})[n]_q-nt}. \end{align} $$
Then, for every
![]() $j=0,1,2,\ldots ,$
$j=0,1,2,\ldots ,$
 $$ \begin{align} \sum_{k=0}^{n-1}(q^{\,j+k}+t)(1+z(q^{k-n+1}-1))=\gamma(1+z(q^{\,j-n+1}-1)). \end{align} $$
$$ \begin{align} \sum_{k=0}^{n-1}(q^{\,j+k}+t)(1+z(q^{k-n+1}-1))=\gamma(1+z(q^{\,j-n+1}-1)). \end{align} $$
Proof. Since
![]() $\gamma ^2-(nt+[n]_{q^2})\gamma +t(n[n]_{q^2}-[n]_q^2)=0,$
we have
$\gamma ^2-(nt+[n]_{q^2})\gamma +t(n[n]_{q^2}-[n]_q^2)=0,$
we have
For
![]() $j\in \{0,1,2,\ldots \}$
, set
$j\in \{0,1,2,\ldots \}$
, set
 $$ \begin{align*}R_{j}=\sum_{k=0}^{n-1}(q^{\,j+k}+t)(1+z(q^{k-n+1}-1))-\gamma(1+z(q^{\,j-n+1}-1)).\end{align*} $$
$$ \begin{align*}R_{j}=\sum_{k=0}^{n-1}(q^{\,j+k}+t)(1+z(q^{k-n+1}-1))-\gamma(1+z(q^{\,j-n+1}-1)).\end{align*} $$
It is easy to see that
 $$ \begin{align*} \begin{aligned} R_{j}-\sum_{k=0}^{n-1}t(1+z(q^{k-n+1}-1))+\gamma(1-z) =q^{\,j-n+1}\big({q^{n-1}[n]_q(1-z)+z[n]_{q^2}}-\gamma z\big)=0 \end{aligned}\end{align*} $$
$$ \begin{align*} \begin{aligned} R_{j}-\sum_{k=0}^{n-1}t(1+z(q^{k-n+1}-1))+\gamma(1-z) =q^{\,j-n+1}\big({q^{n-1}[n]_q(1-z)+z[n]_{q^2}}-\gamma z\big)=0 \end{aligned}\end{align*} $$
with the aid of (3.3). So
![]() $R_0=R_1=\cdots $
. As
$R_0=R_1=\cdots $
. As
 $$ \begin{align*} \sum_{k=0}^{n-1}(q^{n-1+k}+t)(1+z(q^{k-n+1}-1)) =\gamma=\gamma(1+z(q^{(n-1)-n+1}-1)), \end{align*} $$
$$ \begin{align*} \sum_{k=0}^{n-1}(q^{n-1+k}+t)(1+z(q^{k-n+1}-1)) =\gamma=\gamma(1+z(q^{(n-1)-n+1}-1)), \end{align*} $$
we get
![]() $R_{n-1}=0$
. So the desired result follows.
$R_{n-1}=0$
. So the desired result follows.
Proof of Theorem 1.5.
It is easy to verify the desired result for
![]() $n=2$
. Below we assume that
$n=2$
. Below we assume that
![]() $n\ge 3$
.
$n\ge 3$
.
If
![]() $[n]_{q^2}-q^{n-1}[n]_q$
and
$[n]_{q^2}-q^{n-1}[n]_q$
and
![]() $q^{1-n}[n]_q-n$
are both zero, then
$q^{1-n}[n]_q-n$
are both zero, then
![]() $[n]_q\not =0$
and
$[n]_q\not =0$
and
and hence
![]() $q^{n-1}=1$
and
$q^{n-1}=1$
and
![]() $n=[n]_q=1$
. As
$n=[n]_q=1$
. As
![]() $n\ge 3$
, there are infinitely many
$n\ge 3$
, there are infinitely many
![]() $t\in \mathbb C$
such that
$t\in \mathbb C$
such that
Take such a number t, and choose
![]() $\gamma $
and z as in (3.1). Then
$\gamma $
and z as in (3.1). Then
![]() $\gamma $
given in (3.1) is an eigenvalue of the matrix
$\gamma $
given in (3.1) is an eigenvalue of the matrix
![]() $Q=[q^{\,j+k}+t]_{0\le \,j,k\le n-1}$
, and the column vector
$Q=[q^{\,j+k}+t]_{0\le \,j,k\le n-1}$
, and the column vector
![]() $v=(v_0,\ldots ,v_{n-1})^T$
with
$v=(v_0,\ldots ,v_{n-1})^T$
with
![]() $v_k=1+z(q^{k-n+1}-1)$
is an eigenvector of Q associated with the eigenvalue
$v_k=1+z(q^{k-n+1}-1)$
is an eigenvector of Q associated with the eigenvalue
![]() $\gamma $
. There are two different choices for
$\gamma $
. There are two different choices for
![]() $\gamma $
since
$\gamma $
since
![]() $(nt-[n]_{q^2})^2+4t[n]_q^2\not =0$
.
$(nt-[n]_{q^2})^2+4t[n]_q^2\not =0$
.
Let
![]() $s\in \{3,\ldots ,n\}$
. For
$s\in \{3,\ldots ,n\}$
. For
![]() $k\in \{0,\ldots ,n-1\}$
, define
$k\in \{0,\ldots ,n-1\}$
, define
 $$ \begin{align*}v^{(s)}_k= \begin{cases} q[s-2]_q&\text{if}\ k=0, \\ -[s-1]_q&\text{if}\ k=1, \\ \delta_{s,k+1}&\text{if}\ 2\le k\le n-1. \end{cases}\end{align*} $$
$$ \begin{align*}v^{(s)}_k= \begin{cases} q[s-2]_q&\text{if}\ k=0, \\ -[s-1]_q&\text{if}\ k=1, \\ \delta_{s,k+1}&\text{if}\ 2\le k\le n-1. \end{cases}\end{align*} $$
It is easy to verify that
 $$ \begin{align*}\sum_{k=0}^{n-1}v^{(s)}_k=0=\sum_{k=0}^{n-1}q^{\,j+k}v^{(s)}_k\quad \text{for all}\ j=1,\ldots,n.\end{align*} $$
$$ \begin{align*}\sum_{k=0}^{n-1}v^{(s)}_k=0=\sum_{k=0}^{n-1}q^{\,j+k}v^{(s)}_k\quad \text{for all}\ j=1,\ldots,n.\end{align*} $$
Thus,
![]() $0$
is an eigenvalue of the matrix
$0$
is an eigenvalue of the matrix
![]() $Q=[q^{\,j+k}+t]_{0\le \,j,k\le {n-1}}$
, and the column vector
$Q=[q^{\,j+k}+t]_{0\le \,j,k\le {n-1}}$
, and the column vector
![]() $v^{(s)}=(v^{(s)}_0,\ldots ,v^{(s)}_{n-1})^T$
is an eigenvector of Q associated with the eigenvalue
$v^{(s)}=(v^{(s)}_0,\ldots ,v^{(s)}_{n-1})^T$
is an eigenvector of Q associated with the eigenvalue
![]() $0$
.
$0$
.
If
![]() $\sum _{s=3}^{n} c_sv^{(s)}$
is the zero column vector for some
$\sum _{s=3}^{n} c_sv^{(s)}$
is the zero column vector for some
![]() $c_3,\ldots ,c_{n}\in \mathbb C$
, then for each
$c_3,\ldots ,c_{n}\in \mathbb C$
, then for each
![]() $k=2,\ldots ,n-1$
,
$k=2,\ldots ,n-1$
,
 $$ \begin{align*} c_{k+1}=\sum_{s=3}^{n} c_s\delta_{s,k+1}=\sum_{s=3}^{n} c_sv^{(s)}_{k}=0. \end{align*} $$
$$ \begin{align*} c_{k+1}=\sum_{s=3}^{n} c_s\delta_{s,k+1}=\sum_{s=3}^{n} c_sv^{(s)}_{k}=0. \end{align*} $$
Thus, the
![]() $n-2$
column vectors
$n-2$
column vectors
![]() $v^{(3)},\ldots ,v^{(n)}$
are linearly independent over
$v^{(3)},\ldots ,v^{(n)}$
are linearly independent over
![]() $\mathbb C$
.
$\mathbb C$
.
By the above, the n eigenvalues of the matrix
![]() $Q=[q^{\,j+k}+t]_{0\le \,j,k\le {n-1}}$
are the two values of
$Q=[q^{\,j+k}+t]_{0\le \,j,k\le {n-1}}$
are the two values of
![]() $\gamma $
given by (3.2) and
$\gamma $
given by (3.2) and
![]() $\lambda _3=\cdots =\lambda _n=0$
. Thus, the characteristic polynomial of Q is
$\lambda _3=\cdots =\lambda _n=0$
. Thus, the characteristic polynomial of Q is
 $$ \begin{align*}\det(xI_n-Q)=&\ \bigg(x-\frac{nt+[n]_{q^2}}2-\frac{\sqrt{(nt-[n]_{q^2})^2+4t[n]_q^2}}2\bigg) \\&\ \times\bigg(x-\frac{nt+[n]_{q^2}}2+\frac{\sqrt{(nt-[n]_{q^2})^2+4t[n]_q^2}}2\bigg)\prod_{s=3}^n(x-\lambda_s) \\=&\ x^{n-2}\bigg(\bigg(x-\frac{nt+[n]_{q^2}}2\bigg)^2-\frac{(nt-[n]_{q^2})^2+4t[n]_q^2}4\bigg) \\=&\ x^n-(nt+[n]_{q^2})x^{n-1}+(n[n]_{q^2}-[n]_q^2)tx^{n-2}. \end{align*} $$
$$ \begin{align*}\det(xI_n-Q)=&\ \bigg(x-\frac{nt+[n]_{q^2}}2-\frac{\sqrt{(nt-[n]_{q^2})^2+4t[n]_q^2}}2\bigg) \\&\ \times\bigg(x-\frac{nt+[n]_{q^2}}2+\frac{\sqrt{(nt-[n]_{q^2})^2+4t[n]_q^2}}2\bigg)\prod_{s=3}^n(x-\lambda_s) \\=&\ x^{n-2}\bigg(\bigg(x-\frac{nt+[n]_{q^2}}2\bigg)^2-\frac{(nt-[n]_{q^2})^2+4t[n]_q^2}4\bigg) \\=&\ x^n-(nt+[n]_{q^2})x^{n-1}+(n[n]_{q^2}-[n]_q^2)tx^{n-2}. \end{align*} $$
Thus, the identity (1.4) holds for infinitely many values of t. Note that both sides of (1.4) are polynomials in t for any fixed
![]() $x\in \mathbb C$
. If we view both sides of (1.4) as polynomials in x and t, then the identity (1.4) still holds. This concludes the proof.
$x\in \mathbb C$
. If we view both sides of (1.4) as polynomials in x and t, then the identity (1.4) still holds. This concludes the proof.
4. Proof of Theorem 1.7
Proof of Theorem 1.7.
If
![]() $w_0=w_1=0$
or
$w_0=w_1=0$
or
![]() $n=2$
, then the desired result can be easily verified. Below we assume that
$n=2$
, then the desired result can be easily verified. Below we assume that
![]() $n\ge 3$
and
$n\ge 3$
and
![]() $\{w_0,w_1\}\not =\{0\}$
.
$\{w_0,w_1\}\not =\{0\}$
.
Let
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
be the two roots of the quadratic equation
$\beta $
be the two roots of the quadratic equation
![]() $z^2-az+b=0$
. Note that
$z^2-az+b=0$
. Note that
![]() $\alpha \beta =b\not =0$
. Also,
$\alpha \beta =b\not =0$
. Also,
![]() $\alpha \not =\beta $
since
$\alpha \not =\beta $
since
![]() $\Delta =a^2-4b$
is nonzero. It is well known that there are constants
$\Delta =a^2-4b$
is nonzero. It is well known that there are constants
![]() $c_1,c_2\in \mathbb C$
such that
$c_1,c_2\in \mathbb C$
such that
![]() $w_m=c_1\alpha ^m+c_2\beta ^m$
for all
$w_m=c_1\alpha ^m+c_2\beta ^m$
for all
![]() $m\in \mathbb Z$
. As
$m\in \mathbb Z$
. As
![]() $c_1+c_2=w_0$
and
$c_1+c_2=w_0$
and
![]() $c_1\alpha +c_2\beta =w_1$
,
$c_1\alpha +c_2\beta =w_1$
,
Since
![]() $w_0$
or
$w_0$
or
![]() $w_1$
is nonzero, one of
$w_1$
is nonzero, one of
![]() $c_1$
and
$c_1$
and
![]() $c_2$
is nonzero. Without any loss of generality, we assume
$c_2$
is nonzero. Without any loss of generality, we assume
![]() $c_1\not =0$
.
$c_1\not =0$
.
Let W denote the matrix
![]() $[w_{\,j-k}+c\delta _{jk}]_{1\le \,j,k\le n}$
. Then
$[w_{\,j-k}+c\delta _{jk}]_{1\le \,j,k\le n}$
. Then
 $$ \begin{align*}\det(W) & = \det[c_1\alpha^{\,j-k}+c_2\beta^{\,j-k}+c\delta_{jk}]_{1\le \,j,k\le n} \\ & =c_1^n\prod_{\,j=1}^n\beta^{\,j}\times\prod_{k=1}^n\beta^{-k} \times\det\bigg[\bigg(\frac{\alpha}{\beta}\bigg)^{\,j-k}+\frac{c_2+c\delta_{jk}\beta^{k-\,j}}{c_1}\bigg]_{1\le \,j,k\le n} \\ & = c_1^n\det[q^{\,j-k}+t-x\delta_{jk}]_{1\le \,j,k\le n}=(-c_1)^n\det[x\delta_{jk}-q^{\,j-k}-t]_{1\le \,j,k\le n}, \end{align*} $$
$$ \begin{align*}\det(W) & = \det[c_1\alpha^{\,j-k}+c_2\beta^{\,j-k}+c\delta_{jk}]_{1\le \,j,k\le n} \\ & =c_1^n\prod_{\,j=1}^n\beta^{\,j}\times\prod_{k=1}^n\beta^{-k} \times\det\bigg[\bigg(\frac{\alpha}{\beta}\bigg)^{\,j-k}+\frac{c_2+c\delta_{jk}\beta^{k-\,j}}{c_1}\bigg]_{1\le \,j,k\le n} \\ & = c_1^n\det[q^{\,j-k}+t-x\delta_{jk}]_{1\le \,j,k\le n}=(-c_1)^n\det[x\delta_{jk}-q^{\,j-k}-t]_{1\le \,j,k\le n}, \end{align*} $$
where
![]() $q=\alpha /\beta \not =0,1$
,
$q=\alpha /\beta \not =0,1$
,
![]() $t=c_2/c_1$
and
$t=c_2/c_1$
and
![]() $x=-c/c_1$
. By applying Theorem 1.1, we obtain
$x=-c/c_1$
. By applying Theorem 1.1, we obtain
 $$ \begin{align*}\det(W)&=(-c_1)^n x^{n-2}(x^2-n(t+1)x+t(n^2-q^{1-n}[n]_q^2)) \\ &=c^{n-2}\bigg(c^2+nc(c_1+c_2)+c_1c_2\bigg(n^2-\frac{\alpha^{1-n}}{\beta^{1-n}}\bigg(\frac{(\alpha/\beta)^n-1}{\alpha/\beta-1}\bigg)^2\bigg)\bigg) \\ &=c^n+nw_0c^{n-1}+c^{n-2}c_1c_2\bigg(n^2-(\alpha\beta)^{1-n}\bigg(\frac{\alpha^n-\beta^n}{\alpha-\beta}\bigg)^2\bigg) \\ &=c^n+nw_0c^{n-1}+c^{n-2}c_1c_2(n^2-b^{1-n}u_n(a,b)^2). \end{align*} $$
$$ \begin{align*}\det(W)&=(-c_1)^n x^{n-2}(x^2-n(t+1)x+t(n^2-q^{1-n}[n]_q^2)) \\ &=c^{n-2}\bigg(c^2+nc(c_1+c_2)+c_1c_2\bigg(n^2-\frac{\alpha^{1-n}}{\beta^{1-n}}\bigg(\frac{(\alpha/\beta)^n-1}{\alpha/\beta-1}\bigg)^2\bigg)\bigg) \\ &=c^n+nw_0c^{n-1}+c^{n-2}c_1c_2\bigg(n^2-(\alpha\beta)^{1-n}\bigg(\frac{\alpha^n-\beta^n}{\alpha-\beta}\bigg)^2\bigg) \\ &=c^n+nw_0c^{n-1}+c^{n-2}c_1c_2(n^2-b^{1-n}u_n(a,b)^2). \end{align*} $$
In view of (4.1),
 $$ \begin{align*} c_1c_2=\frac{(w_1-\beta w_0)(\alpha w_0-w_1)}{(\alpha-\beta)^2}=\frac{-w_1^2+(\alpha+\beta)w_0w_1-\alpha\beta w_0^2}{\Delta}=-\frac{w_1^2-aw_0w_1+bw_0^2}{a^2-4b}. \end{align*} $$
$$ \begin{align*} c_1c_2=\frac{(w_1-\beta w_0)(\alpha w_0-w_1)}{(\alpha-\beta)^2}=\frac{-w_1^2+(\alpha+\beta)w_0w_1-\alpha\beta w_0^2}{\Delta}=-\frac{w_1^2-aw_0w_1+bw_0^2}{a^2-4b}. \end{align*} $$
Therefore, the desired evaluation (1.6) follows.