Article contents
THE SECOND SHIFTED DIFFERENCE OF PARTITIONS AND ITS APPLICATIONS
Published online by Cambridge University Press: 25 August 2022
Abstract
A number of recent papers have estimated ratios of the partition function 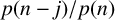 $p(n-j)/p(n)$, which appear in many applications. Here, we prove an easy-to-use effective bound on these ratios. Using this, we then study the second shifted difference of partitions,
$p(n-j)/p(n)$, which appear in many applications. Here, we prove an easy-to-use effective bound on these ratios. Using this, we then study the second shifted difference of partitions, 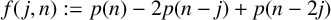 $f(\,j,n) := p(n) -2p(n-j) +p(n-2j)$, and give another easy-to-use estimate of
$f(\,j,n) := p(n) -2p(n-j) +p(n-2j)$, and give another easy-to-use estimate of 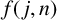 $f(\,j,n)$. As applications of these, we prove a shifted convexity property of
$f(\,j,n)$. As applications of these, we prove a shifted convexity property of 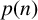 $p(n)$, as well as giving new estimates of the k-rank partition function
$p(n)$, as well as giving new estimates of the k-rank partition function 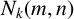 $N_k(m,n)$ and non-k-ary partitions along with their differences.
$N_k(m,n)$ and non-k-ary partitions along with their differences.
MSC classification
Information
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 107 , Issue 1 , February 2023 , pp. 66 - 78
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.
Footnotes
The research of the second author conducted for this paper is supported by the Pacific Institute for the Mathematical Sciences (PIMS). The research and findings may not reflect those of the Institute. This work was supported by a grant from the Simons Foundation (853830, LR). The third author is also grateful for support from a 2021–2023 Dean’s Faculty Fellowship from Vanderbilt University and to the Max Planck Institute for Mathematics in Bonn for its hospitality and financial support.
References
- 1
- Cited by


