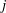 $j$-WISE RELATIVELY
$j$-WISE RELATIVELY  $r$-PRIME ALGEBRAIC INTEGERS
$r$-PRIME ALGEBRAIC INTEGERSPublished online by Cambridge University Press: 06 July 2018
Let 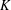 $K$ be a number field with a ring of integers
$K$ be a number field with a ring of integers 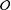 ${\mathcal{O}}$. We follow Ferraguti and Micheli [‘On the Mertens–Cèsaro theorem for number fields’, Bull. Aust. Math. Soc.93(2) (2016), 199–210] to define a density for subsets of
${\mathcal{O}}$. We follow Ferraguti and Micheli [‘On the Mertens–Cèsaro theorem for number fields’, Bull. Aust. Math. Soc.93(2) (2016), 199–210] to define a density for subsets of 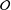 ${\mathcal{O}}$ and use it to find the density of the set of
${\mathcal{O}}$ and use it to find the density of the set of 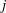 $j$-wise relatively
$j$-wise relatively  $r$-prime
$r$-prime 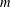 $m$-tuples of algebraic integers. This provides a generalisation and analogue for several results on natural densities of integers and ideals of algebraic integers.
$m$-tuples of algebraic integers. This provides a generalisation and analogue for several results on natural densities of integers and ideals of algebraic integers.