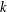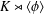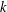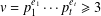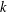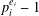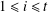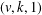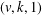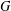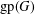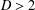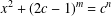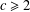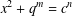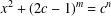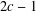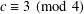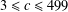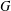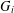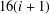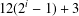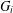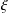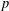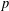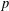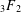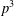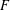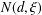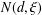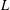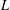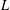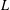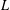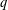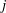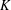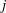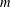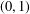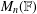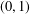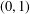Research Article
RESOLVABLE MENDELSOHN DESIGNS AND FINITE FROBENIUS GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 30 May 2018, pp. 1-13
-
- Article
-
- You have access
- Export citation
A GENERAL POSITION PROBLEM IN GRAPH THEORY
- Part of:
-
- Published online by Cambridge University Press:
- 18 July 2018, pp. 177-187
-
- Article
-
- You have access
- Export citation
DETERMINING CROSSING NUMBERS OF GRAPHS OF ORDER SIX USING CYCLIC PERMUTATIONS
- Part of:
-
- Published online by Cambridge University Press:
- 17 August 2018, pp. 353-362
-
- Article
-
- You have access
- Export citation
ON THE TOTAL DISTANCE AND DIAMETER OF GRAPHS
- Part of:
-
- Published online by Cambridge University Press:
- 03 May 2018, pp. 14-17
-
- Article
-
- You have access
- Export citation
A NOTE ON THE DIOPHANTINE EQUATION
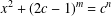 $x^{2}+(2c-1)^{m}=c^{n}$
$x^{2}+(2c-1)^{m}=c^{n}$
- Part of:
-
- Published online by Cambridge University Press:
- 12 July 2018, pp. 188-195
-
- Article
-
- You have access
- Export citation
A STRUCTURED INVERSE SPECTRUM PROBLEM FOR INFINITE GRAPHS AND UNBOUNDED OPERATORS
- Part of:
-
- Published online by Cambridge University Press:
- 15 August 2018, pp. 363-371
-
- Article
-
- You have access
- Export citation
SOME HYPERGEOMETRIC INTEGRALS FOR LINEAR FORMS IN ZETA VALUES
- Part of:
-
- Published online by Cambridge University Press:
- 19 July 2018, pp. 372-375
-
- Article
-
- You have access
- Open access
- Export citation
A SIMPLE PROOF OF CHEBOTAREV’S DENSITY THEOREM OVER FINITE FIELDS
- Part of:
-
- Published online by Cambridge University Press:
- 12 July 2018, pp. 196-202
-
- Article
-
- You have access
- Export citation
THE COMPLEXITY OF THOMASON’S ALGORITHM FOR FINDING A SECOND HAMILTONIAN CYCLE
- Part of:
-
- Published online by Cambridge University Press:
- 03 May 2018, pp. 18-26
-
- Article
-
- You have access
- Export citation
ON THE ABSENCE OF ZEROS IN INFINITE ARITHMETIC PROGRESSION FOR CERTAIN ZETA FUNCTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 15 August 2018, pp. 376-382
-
- Article
-
- You have access
- Export citation
ON MAHLER’S CLASSIFICATION OF
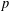 $p$-ADIC NUMBERS
$p$-ADIC NUMBERS
- Part of:
-
- Published online by Cambridge University Press:
- 30 July 2018, pp. 203-211
-
- Article
-
- You have access
- Export citation
SUPERCONGRUENCES INVOLVING
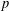 $p$-ADIC GAMMA FUNCTIONS
$p$-ADIC GAMMA FUNCTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 30 May 2018, pp. 27-37
-
- Article
-
- You have access
- Export citation
COMMON SLOTS OF BILINEAR AND QUADRATIC PFISTER FORMS
- Part of:
-
- Published online by Cambridge University Press:
- 03 May 2018, pp. 38-47
-
- Article
-
- You have access
- Export citation
ALGEBRAIC NUMBERS WITH BOUNDED DEGREE AND WEIL HEIGHT
- Part of:
-
- Published online by Cambridge University Press:
- 18 July 2018, pp. 212-220
-
- Article
-
- You have access
- Export citation
THE RECIPROCITY LAW FOR THE TWISTED SECOND MOMENT OF DIRICHLET
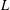 $L$-FUNCTIONS OVER RATIONAL FUNCTION FIELDS
$L$-FUNCTIONS OVER RATIONAL FUNCTION FIELDS
- Part of:
-
- Published online by Cambridge University Press:
- 28 August 2018, pp. 383-388
-
- Article
-
- You have access
- Export citation
A NOTE ON GUNNINGHAM’S FORMULA
- Part of:
-
- Published online by Cambridge University Press:
- 01 August 2018, pp. 389-401
-
- Article
-
- You have access
- Export citation
THETA BLOCK FOURIER EXPANSIONS, BORCHERDS PRODUCTS AND A SEQUENCE OF NEWMAN AND SHANKS
- Part of:
-
- Published online by Cambridge University Press:
- 14 June 2018, pp. 48-59
-
- Article
-
- You have access
- Export citation
THE DENSITY OF
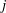 $j$-WISE RELATIVELY
$j$-WISE RELATIVELY  $r$-PRIME ALGEBRAIC INTEGERS
$r$-PRIME ALGEBRAIC INTEGERS
- Part of:
-
- Published online by Cambridge University Press:
- 06 July 2018, pp. 221-229
-
- Article
-
- You have access
- Export citation
LIFTINGS OF A MONOMIAL CURVE
- Part of:
-
- Published online by Cambridge University Press:
- 05 July 2018, pp. 230-238
-
- Article
-
- You have access
- Export citation
ON MINIMAL SETS OF
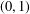 $(0,1)$-MATRICES WHOSE PAIRWISE PRODUCTS FORM A BASIS FOR
$(0,1)$-MATRICES WHOSE PAIRWISE PRODUCTS FORM A BASIS FOR 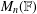 $M_{n}(\mathbb{F})$
$M_{n}(\mathbb{F})$
- Part of:
-
- Published online by Cambridge University Press:
- 28 August 2018, pp. 402-413
-
- Article
-
- You have access
- Export citation