A PAIR OF EQUATIONS IN EIGHT PRIME CUBES AND POWERS OF 2

Abstract

In this paper, we show that every pair of sufficiently large even integers can be represented as a pair of eight prime cubes and k powers of 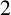$2$. In particular, we prove that 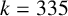$k=335$ is admissible, which improves the previous result.

1 Introduction

In 1951 and 1953, Linnik [5, 6] showed that every large even integer N can be represented in the form of two primes and a bounded number of powers of 2, namely

(1.1) $$ \begin{align} N'=p_{1}+p_{2}+2^{v_{1}}+2^{v_{2}}+\cdots+2^{v_{k'}}. \end{align} $$

Later, Liu et al. [8] proved that $k'=54000$ is acceptable in (1.1). After many improvements, up to now, the best result is $k'=8$ established by Pintz and Ruzsa [14]. In 2013, Kong [3] first considered the simultaneous representation of pairs of positive even integers as sums of two primes and powers of $2$ , that is,

$$ \begin{align*} \begin{cases} N_{1}'=p_{1}+p_{2}+2^{v_{1}}+2^{v_{2}}+\cdots +2^{v_{k'}}, \\ N_{2}'=p_{3}+p_{4}+2^{v_{1}}+2^{v_{2}}+\cdots +2^{v_{k'}}. \end{cases} \end{align*} $$

She proved that these equations are solvable for a pair of sufficiently large positive even integers $N_{1}'$ and $N_{2}'$ satisfying $N_{2}'\gg N_{1}'> N_{2}'$ for $k'=63$ unconditionally, and for $k'=31$ under the generalised Riemann hypothesis (GRH). Subsequently, Kong and Liu [4] improved the value of $k'$ to $34$ unconditionally and to $18$ under the GRH.

In 2001, based on the works of Linnik [5, 6] and Gallagher [2], Liu and Liu [7] proved that every large even integer N can be written as a sum of eight cubes of primes and a bounded number of powers of $2$ , namely

$$ \begin{align*} N=p_{1}^{3}+p_{2}^{3}+\cdots+p_{8}^{3}+2^{v_{1}}+2^{v_{2}}+\cdots+2^{v_{k}}. \end{align*} $$

So far, the best result for this equation is $k=30$ obtained by Zhu [19].

As a generalisation, in 2013, Liu [11] first considered the simultaneous representation of pairs of positive even integers $N_{1}$ and $N_{2}$ satisfying $N_{2}\gg N_{1}> N_{2}$ in the form

(1.2) $$ \begin{align} \begin{cases} N_{1}=p_{1}^{3}+p_{2}^{3}+\cdots+p_{8}^{3}+2^{v_{1}}+2^{v_{2}}+\cdots +2^{v_{k}}, \\ N_{2}=p_{9}^{3}+p_{10}^{3}+\cdots+p_{16}^{3}+2^{v_{1}}+2^{v_{2}}+\cdots +2^{v_{k}}, \end{cases} \end{align} $$

where k is a positive integer. Liu [11] proved that the equations in (1.2) are solvable for $k = 1432$ . This number k was improved successively to $ k=1364, k=658$ and $k=609$ by Platt and Trudgian [15], Zhao [17] and Liu [9], respectively. We make a further improvement on the value of k in (1.2) by establishing the following result.

Theorem 1.1. For $k=335$ , the equations in (1.2) are solvable for every pair of sufficiently large positive even integers $N_{1}$ and $N_{2}$ satisfying $N_{2}\gg N_{1}>N_{2}$ .

To prove Theorem 1.1, we apply the circle method in combination with some new arguments of Kong and Liu [4]. To apply the circle method, similarly to [4], we divide $[0,1]^{2}$ into three arcs, which means we can avoid the limitation of two arcs in Liu [9] after applying integral transforms (see Section 4 for details), resulting in the sharper k in (1.2).

Notation 1.2. Throughout this paper, the letter p, with or without a subscript, always represents a prime. Both $N_{1}$ and $N_{2}$ denote sufficiently large positive even integers, $e(x)=\exp (2\pi ix)$ and $n\sim N$ means $N<n\leq 2N$ . The letter $\epsilon $ denotes a positive constant which is arbitrarily small but may not be the same at different occurrences.

2 Outline of the proof

In this section, we give an outline for the proof of Theorem 1.1. To apply the circle method, we let, for $i=1,2$ ,

$$ \begin{align*} P_{i}=N_{i}^{{1}/{9}-2\epsilon}, \quad Q_{i}=N_{i}^{{8}/{9}+\epsilon},\quad L=\frac{\log(N_{1}/\log N_{1})}{\log 2}. \end{align*} $$

For $i=1,2$ , we define the major arcs $\mathfrak {M}_{i}$ and minor arcs $C(\mathfrak {M}_{i})$ as

(2.1) $$ \begin{align} \mathfrak{M}_{i}=\bigcup_{1 \leq q_{i} \leq P_{i}}\bigcup_{\substack{1 \leq a_{i} \leq q_{i} \\ (a_{i}, q_{i})=1}}{ } \mathfrak{M}_{i}(a_{i}, q_{i}),\quad C(\mathfrak{M}_{i})=[0,1] \backslash \mathfrak{M}_{i}, \end{align} $$

where

$$ \begin{align*} \mathfrak{M}_{i}(a_{i}, q_{i})=\bigg\{\alpha_{i} \in[0,1]:\bigg|\alpha_{i}-\frac{a_{i}}{q_{i}}\bigg| \leq \frac{1}{q_{i} Q_{i}}\bigg\} \end{align*} $$

and

$$ \begin{align*} 1\leq a_{i}\leq q_{i}\leq Q_{i}, \quad (a_{i},q_{i})=1. \end{align*} $$

Note that the major arcs $\mathfrak {M}_{i}(a_{i}, q_{i})$ are mutually disjoint since $2P_{i}\leq Q_{i}$ . We further define

(2.2) $$ \begin{align} \mathfrak{M}=\mathfrak{M}_{1} \times \mathfrak{M}_{2}=\{(\alpha_{1}, \alpha_{2}) \in[0,1]^{2}: \alpha_{1} \in \mathfrak{M}_{1}, \alpha_{2} \in \mathfrak{M}_{2}\}, \end{align} $$

(2.3) $$ \begin{align} C(\mathfrak{M})=[0,1]^{2} \backslash \mathfrak{M}. \end{align} $$

As in [16], let $\delta =10^{-4}$ and

$$ \begin{align*} U_{i}=\bigg(\frac{N_{i}}{16(1+\delta)}\bigg)^{{1}/{3}}, \quad V_{i}=U_{i}^{{5}/{6}}. \end{align*} $$

For $i=1,2$ , we set

(2.4) $$ \begin{align} S(\alpha_{i},U_{i})=\sum_{p \sim U_{i}}(\log p) e(p^{3} \alpha_{i}), \quad T(\alpha_{i},V_{i})=\sum_{p \sim V_{i}}(\log p) e(p^{3} \alpha_{i}), \end{align} $$

$$ \begin{align*} G(\alpha_{i})=\sum_{4 \leq v \leq L} e(2^{v} \alpha_{i}), \quad \mathscr{E}_{\lambda}=\{(\alpha_{1},\alpha_{2})\in[0,1]^{2}:|G(\alpha_{1}+\alpha_{2})|\geq \lambda L\}. \end{align*} $$

Let

$$ \begin{align*} R(N_{1},N_{2})=\sum\log p_{1}\log p_{2}\cdots\log p_{16} \end{align*} $$

be the weighted number of solutions of (1.2) in $(p_{1},p_{2},\ldots ,p_{16},v_{1},v_{2},\ldots ,v_{k})$ with

$$ \begin{align*} \begin{aligned} p_{1},p_{2},p_{3},p_{4} \sim U_{1}, \quad &p_{5},p_{6},p_{7},p_{8} \sim V_{1}, \\ p_{9},p_{10},p_{11},p_{12} \sim U_{2}, \quad &p_{13},p_{14},p_{15},p_{16} \sim V_{2},\\ 4 \leq v_{j} \leq L, \quad &j=1,2, \ldots, k. \end{aligned} \end{align*} $$

Then we rewrite $R(N_{1},N_{2})$ as

$$ \begin{align*} \begin{aligned} R(N_{1}, N_{2}) =&\,\bigg(\iint_{\mathfrak{M}}+\iint_{C(\mathfrak{M}) \cap \mathscr{E}_{\lambda}}+\iint_{C(\mathfrak{M}) \backslash \mathscr{E}_{\lambda}}\bigg) \,S^{4}(\alpha_{1}, U_{1})T^{4}(\alpha_{1}, V_{1})S^{4}(\alpha_{2},U_{2})T^{4}(\alpha_{2}, V_{2}) \\ &\quad \times G^{k}(\alpha_{1}+\alpha_{2}) e(-\alpha_{1} N_{1}-\alpha_{2} N_{2})\,{d}\alpha_{1}\,{d}\alpha_{2} \\ :=&\,R_{1}(N_{1}, N_{2})+R_{2}(N_{1}, N_{2})+R_{3}(N_{1}, N_{2}). \end{aligned} \end{align*} $$

In Section 3, we first give some lemmas. In Section 4, we shall estimate $R_{i}(N_{1}, N_{2})$ for $i=1,2,3$ and complete the proof of Theorem 1.1.

3 Auxiliary lemmas

Let

(3.1) $$ \begin{align} C(q, a)=\sum_{\substack{m=1 \\ (m,q)=1}}^{q} e\bigg(\frac{a m^{3}}{q}\bigg), &\quad B(n,q)=\sum_{\substack{a=1\\ (a, q)=1}}^{q} C^{8}(q, a) e\bigg(-\frac{a n}{q}\bigg), \nonumber\\[-6pt] \\[-6pt]A(n, q)=\frac{B(n, q)}{ \varphi^{8}(q)},&\quad \mathfrak{S}(n)=\sum_{q=1}^{\infty} A(n, q). \nonumber\end{align} $$

Lemma 3.1. Let $\mathscr {A}(N_{i},k)=\{n_{i}\geq 2: n_{i}=N_{i}-2^{v_{1}}-2^{v_{2}}-\cdots -2^{v_{k}}\}$ with $k\geq 35$ . Then, for $N_{1} \equiv N_{2} \equiv 0\ ( \bmod \ 2)$ ,

$$ \begin{align*} \sum_{\substack{n_{1} \in \mathscr{A}(N_{1}, k)\\n_{2} \in \mathscr{A}(N_{2}, k)\\ n_{1} \equiv n_{2} \equiv 0 \pmod 2}} \mathfrak{S}(n_{1}) \mathfrak{S}(n_{2}) \geq 0.1596600336 L^{k}. \end{align*} $$

Proof. From (5.9) of [12] and Lemma 2.3 of [18], for $p\geq 13 \text { and } p \equiv 1 \ ( \bmod \ 3)$ ,

$$ \begin{align*} 1+A(n,p)\geq 1-\frac{(2\sqrt{p}+1)^{8}}{(p-1)^{7}}, \end{align*} $$

and

$$ \begin{align*} \prod_{p \geq 17}(1+A(n_{i}, p))\geq 0.8206744593. \end{align*} $$

Then,

$$ \begin{align*} \begin{aligned} \prod_{p \geq 13}(1+A(n_{i}, p)) &=(1+A(n_{i}, 13)) \times \prod_{p \geq 17}(1+A(n_{i}, p)) \\ &\geq 0.4233091149\times 0.8206744593\\ &\geq 0.3473989790:=C. \end{aligned} \end{align*} $$

Noting that $\mathfrak {S}(n_{i})=2(1-{1}/{2^{8}})\prod _{p>3}(1+A(n_{i},p))$ and putting $q=\prod _{3<p<12}=385$ ,

$$ \begin{align*} \begin{aligned} \sum_{\substack{n_{1} \in \mathscr{A}(N_{1}, k) \\ n_{2} \in \mathscr{A}(N_{2}, k) \\ n_{1} \equiv n_{2} \equiv 0\ (\!\!\bmod 2)}} & \mathfrak{S}(n_{1}) \mathfrak{S}(n_{2})\\ &\geq\bigg(2\bigg(1-\frac{1}{2^{8}}\bigg) C\bigg)^{2} \sum_{\substack{n_{1} \in \mathscr{A}(N_{1}, k) \\ n_{2} \in \mathscr{A}(N_{2}, k) \\ n_{1} \equiv n_{2} \equiv 0\ (\!\!\bmod 2)}} \prod_{i=1}^{2} \prod_{3<p_{i}<12}(1+A(n_{i}, p_{i}))\\ &\geq\bigg(2\bigg(1-\frac{1}{2^{8}}\bigg) C\bigg)^{2} \sum_{\substack{1 \leq j_{1} \leq q}} \sum_{\substack{1 \leq j_{2} \leq q}}\sum_{\substack{n_{1} \in \mathscr{A}(N_{1}, k) \\ n_{2} \in \mathscr{A}(N_{2}, k) \\ n_{1} \equiv n_{2} \equiv 0\ (\!\!\bmod 2) \\ n_{1} \equiv j_{1}\ (\!\!\bmod q)\\n_{2} \equiv j_{2}\ (\!\!\bmod q)}}\prod_{i=1}^{2} \prod_{3<p_{i}<12}(1+A(\,j_{i}, p_{i}))\\ &\geq\bigg(2\bigg(1-\frac{1}{2^{8}}\bigg) C\bigg)^{2} \sum_{1 \leq j_{1} \leq q} \sum_{1 \leq j_{2} \leq q}\prod_{i=1}^{2} \prod_{3<p_{i}<12}(1+A(\,j_{i}, p_{i})) \sum_{\substack{n_{1} \in \mathscr{A}(N_{1}, k) \\ n_{2} \in \mathscr{A}(N_{2}, k)\\ n_{1} \equiv n_{2} \equiv 0\ (\!\!\bmod 2)\\n_{1} \equiv j_{1}\ (\!\!\bmod q)\\n_{2} \equiv j_{2}\ (\!\!\bmod q)}} 1. \end{aligned} \end{align*} $$

Considering the inner sum,

$$ \begin{align*} S:=\sum_{\substack{n_{1} \in \mathscr{A}(N_{1}, k) \\ n_{2} \in \mathscr{A}(N_{2}, k)\\ n_{1} \equiv n_{2} \equiv 0\ (\!\!\bmod 2)\\n_{1} \equiv j_{1}\ (\!\!\bmod q)\\n_{2} \equiv j_{2}\ (\!\!\bmod q)}} 1=\sum_{\substack{4 \leq v_{j} \leq L, 1 \leq j \leq k, i=1,2\\2^{v_{1}}+2^{v_{2}}+\cdots+2^{v_{k}} \equiv N_{i}\ (\!\!\bmod 2)\\2^{v_{1}}+2^{v_{2}}+\cdots+2^{v_{k}} \equiv N_{i}-j_{i}\ (\!\!\bmod q)}}1. \end{align*} $$

Since $N_{1} \equiv N_{2} \equiv 0\ (\bmod \ 2)$ ,

$$ \begin{align*} \begin{cases} 2^{v_{1}}+2^{v_{2}}+\cdots+2^{v_{k}} \equiv N_{1} \ (\bmod \ 2) \\ 2^{v_{1}}+2^{v_{2}}+\cdots+2^{v_{k}} \equiv N_{2} \ (\bmod \ 2) \end{cases} \end{align*} $$

is equivalent to

$$ \begin{align*} 2^{v_{1}}+2^{v_{2}}+\cdots+2^{v_{k}} \equiv N_{1} \ (\bmod \ 2). \end{align*} $$

Additionally, if $N_{2} \equiv N_{1}+t\ (\bmod \ q)$ and $j_{2} \equiv j_{1}+t\ (\bmod \ q)$ with $1\leq t\leq q$ ,

$$ \begin{align*} \begin{cases} 2^{v_{1}}+2^{v_{2}}+\cdots+2^{v_{k}} \equiv N_{1}-j_{1} \ (\bmod \ q)\\ 2^{v_{1}}+2^{v_{2}}+\cdots+2^{v_{k}} \equiv N_{2}-j_{2} \ (\bmod \ q)\end{cases} \end{align*} $$

is equivalent to

$$ \begin{align*} 2^{v_{1}}+2^{v_{2}}+\cdots+2^{v_{k}} \equiv N_{1}-j_{1} \ (\bmod \ q). \end{align*} $$

Therefore, when $N_{1} \equiv N_{2} \equiv 0\ (\bmod \ 2)$ , $N_{2} \equiv N_{1}+t\ (\bmod \ q)$ and $j_{2} \equiv j_{1}+t\ (\bmod \ q)$ ,

$$ \begin{align*} \begin{aligned} S \geq \sum_{\substack{4 \leq v_{1}, v_{2}, \ldots, v_{k} \leq L \\ 2^{v_{1}}+2^{v_{2}}+\cdots+2^{v_{k}} \equiv N_{1}\ (\!\!\bmod 2)\\2^{v_{1}}+2^{v_{2}}+\cdots+2^{v_{k}} \equiv N_{1}-j_{1}\ (\!\!\bmod q)}} \bigg(\frac{L}{\rho(3 q)}+O(1)\bigg)^{k} \sum_{\substack{4 \leq v_{1},v_{2},\ldots, v_{k} \leq \rho(3 q)\\2^{v_{1}}+2^{v_{2}}+\cdots+2^{v_{k}} \equiv a_{j}\ (\!\!\bmod 3 q)}} 1, \end{aligned} \end{align*} $$

where the natural number $a_{j}\in [1,3q]$ satisfies the conditions $a_{j} \equiv N_{1} \ (\bmod \ 3)$ and $a_{j} \equiv N_{1}-j_{1} \ (\bmod \ q)$ , and $\rho (q)$ denotes the smallest positive integer $\rho $ such that $2^{\rho }\equiv 1 \ (\bmod \ q)$ .

Noting that

$$ \begin{align*} S \geq \frac{1}{3 q}\bigg(\frac{L}{\rho(3 q)}+O(1)\bigg)^{k} \sum_{t=0}^{3 q-1} e\bigg(\frac{t a_{j}}{3q}\bigg)\bigg(\sum_{1 \leq s \leq\rho(3 q)} e\bigg(\frac{t 2^{s}}{3 q}\bigg)\bigg)^{k}, \end{align*} $$

we get

$$ \begin{align*} \begin{aligned} S & \geq \frac{1}{3 q}\bigg(\frac{L}{\rho(3 q)}+O(1)\bigg)^{k}(\,\rho(3 q)^{k}-(3 q-1)(\max )^{k}) \\ &=\frac{L^{k}}{3 q}\bigg(1-(3 q-1)\bigg(\frac{\max }{\rho(3 q)}\bigg)^{k}\bigg)+O(L^{k-1}), \end{aligned} \end{align*} $$

where

$$ \begin{align*} \max =\max \bigg\{\bigg|\sum_{1 \leq s \leq \rho(3 q)} e\bigg(\frac{j 2^{s}}{3 q}\bigg)\bigg|: 1 \leq j \leq 3 q-1\bigg\}. \end{align*} $$

Since $3q=1155$ and $\rho (3q)=60$ , with the help of a computer,

$$ \begin{align*} \max =30\ldots, \quad(3 q-1)\bigg(\frac{\max }{\rho(3 q)}\bigg)^{50}<10^{-10}. \end{align*} $$

Therefore,

$$ \begin{align*} S \geq \frac{(1-10^{-10}) L^{k}}{3 q}+O(L^{k-1}). \end{align*} $$

By a numerical calculation,

$$ \begin{align*} \max _{1 \leq t \leq q}\bigg(\sum_{1 \leq j_{1} \leq q} \prod_{3<p_{1}<12}(1+A(\,j_{1}, p_{1})) \prod_{3<p_{2}<12}(1+A(\,j_{1}+t, p_{2}))\bigg) \geq 384.9999769. \end{align*} $$

Then,

$$ \begin{align*} \sum_{\substack{n_{1} \in \mathscr{A}(N_{1}, k) \\ n_{2} \in \mathscr{A}(N_{2}, k) \\ n_{1} \equiv n_{2} \equiv 0\ (\!\!\bmod 2)}} \mathfrak{S}(n_{1}) \mathfrak{S}(n_{2}) &\geq 384.9999769\bigg(2\bigg(1-\frac{1}{2^{8}}\bigg)C\bigg)^{2}\frac{(1-10^{-10}) L^{k}}{3 q}\\ & \geq 0.1596600336L^{k}.\\[-2.8pc] \end{align*} $$

Lemma 3.2 [12, Lemma 2.1].

Let $\mathfrak {M}_{i}$ , $S(\alpha _{i},U_{i})$ and $T(\alpha _{i},V_{i})$ be defined as in (2.1) and (2.4), respectively. For ${N_{i}}/{2}\leq n_{i}\leq N_{i}$ ,

$$ \begin{align*} \int_{\mathfrak{M}_{i}} S^{4}(\alpha_{i},U_{i}) T^{4}(\alpha_{i},V_{i}) e(-n_{i} \alpha_{i}) \,{d} \alpha_{i}=\frac{1}{3^{8}} \mathfrak{S}(n_{i})\mathfrak{J}(n_{i})+O(N_{i}^{{13}/{9}} L^{-1}), \end{align*} $$

where $\mathfrak {S}(n_{i})$ is defined as in (3.1) and satisfies $\mathfrak {S}(n_{i})\gg 1$ for $n_{i} \equiv 0\ (\bmod \ 2)$ , and $\mathfrak {J}(n_{i})$ is defined as

$$ \begin{align*} \mathfrak{J}(n_{i}):=\sum_{\substack{m_{1}+m_{2}+\cdots+m_{8}=n_{i}\\U_{i}^{3}<m_{1},m_{2},m_{3},m_{4}\leq 8U_{i}^{3}\\V_{i}^{3}<m_{5},m_{6},m_{7},m_{8}\leq 8V_{i}^{3}}}(m_{1}m_{2} \ldots m_{8})^{-{2}/{3}} \end{align*} $$

and satisfies $N_{i}^{{13}/{9}}\ll \mathfrak {J}(n_{i})\ll N_{i}^{{13}/{9}}$ .

Lemma 3.3 [18, Lemma 2.6].

For $(1-\delta )N_{i}\leq n_{i}\leq N_{i}$ ,

$$ \begin{align*} \mathfrak{J}(n_{i})>1.42432055N_{i}^{{13}/{9}}. \end{align*} $$

Lemma 3.4. We have $\operatorname {meas}(\mathscr {E}_{\lambda }) \ll N_{i}^{-E(\lambda )}$ with $E(0.9570253)>\tfrac 89+10^{-10}$ .

Proof. This is (2.7) in Lemma 2.1 of Zhao [17].

Lemma 3.5 [17, Lemma 2.5].

Let $\mathfrak {M}_{i}$ and $S(\alpha _{i},U_{i})$ be defined as in (2.1) and (2.4), respectively. We have

$$ \begin{align*} \max _{\alpha_{i} \in C(\mathfrak{M}_{i})}|S(\alpha_{i},U_{i})| \ll N_{i}^{{11}/{36}+\epsilon}. \end{align*} $$

Lemma 3.6. Let $S(\alpha _{i},U_{i})$ and $T(\alpha _{i},V_{i})$ be defined as in (2.4). We have

$$ \begin{align*} \int_{0}^{1}|S(\alpha_{i},U_{i}) T(\alpha_{i},V_{i})|^{4} \,{d} \alpha_{i} \leq 0.134694091 N_{i}^{{13}/{9}}. \end{align*} $$

Proof. The idea of the proof is similar to that of Lemma 2.6 in Liu and Lü [13]. However, we take $\nu =100552$ obtained by Elsholtz and Schlage-Puchta [1] instead of $147185.22$ obtained by Liu [10]. This leads to a better upper bound.

Here we only consider the case $i=1$ since the case $i=2$ can be proved similarly. From (2.7) of Ren [16] and Proposition 2 of Elsholtz and Schlage-Puchta [1],

$$ \begin{align*} \sum_{{N_{1}}/{9}<l\leq N_{1}}r^{2}(l)\leq \vartheta(0)\leq (\nu+o(1))U_{1}V_{1}^{4}L^{-8}, \end{align*} $$

where $\nu {\kern-1.2pt}={\kern-1.2pt}100552$ , $r(n)$ denotes the number of representations of n as $p_{1}^{3}+p_{2}^{3}+ p_{3}^{3}+p_{4}^{3}$ with $p_{1},p_{2}\sim U_{1}$ , $p_{3},p_{4}\sim V_{1}$ and $\vartheta (0)$ denotes the number of solutions of the equation $p_{1}^{3}+p_{2}^{3}+p_{3}^{3}+p_{4}^{3}=p_{5}^{3}+p_{6}^{3}+p_{7}^{3}+p_{8}^{3}$ with $p_{1},p_{2},p_{5},p_{6} \sim U_{1}, p_{3},p_{4},p_{7}, p_{8} \sim V_{1}$ .

Therefore,

$$ \begin{align*} \begin{split} \int_{0}^{1}|S(\alpha_{1},U_{1}) T(\alpha_{1},V_{1})|^{4} \,{d} \alpha_{1} &\leq (\log (2U_{1}))^{4}(\log(2V_{1}))^{4}\vartheta(0)\\ &\leq 0.134694091N_{1}^{{13}/{9}}. \\[-1.7pc] \end{split} \end{align*} $$

4 Proof of Theorem 1.1

To prove Theorem 1.1, we first estimate $R_{1}(N_{1},N_{2})$ . By Lemmas 3.1, 3.2 and 3.3,

(4.1) $$ \begin{align} R_{1}(N_{1}, N_{2}) & =\iint_{\mathfrak{M}} S^{4}(\alpha_{1}, U_{1})T^{4}(\alpha_{1}, V_{1})S^{4}(\alpha_{2},U_{2})T^{4}(\alpha_{2}, V_{2}) \nonumber\\[4pt] &\quad \times G^{k}(\alpha_{1}+\alpha_{2}) e(-\alpha_{1} N_{1}-\alpha_{2} N_{2}) \,{d} \alpha_{1} \,{d} \alpha_{2} \nonumber\\[4pt] &\geq \bigg(\frac{1}{3^{8}}\bigg)^{2}\sum_{\substack{n_{1}\in\mathscr{A}(N_{1},k)\\n_{2}\in\mathscr{A}(N_{2},k)}}\mathfrak{S}(n_{1})\mathfrak{S}(n_{2}) \mathfrak{J}(n_{1})\mathfrak{J}(n_{2})\\[4pt] &\geq \frac{0.1596600336\times(1.42432055)^{2}}{3^{16}}(N_{1}N_{2})^{{13}/{9}}L^{k}\nonumber\\[4pt] &\geq 7.524395606\times10^{-9}(N_{1}N_{2})^{{13}/{9}}L^{k},\nonumber \end{align} $$

where $\mathfrak {M}$ is defined by (2.2).

Next, we estimate $R_{2}(N_{1},N_{2})$ . By (2.1) and (2.3),

$$ \begin{align*} \begin{aligned} C(\mathfrak{M}) &\subset \{(\alpha_{1}, \alpha_{2}): \alpha_{1} \in C(\mathfrak{M}_{1}), \alpha_{2} \in[0,1]\} \cup\{(\alpha_{1}, \alpha_{2}): \alpha_{1} \in[0,1], \alpha_{2} \in C(\mathfrak{M}_{2})\}. \end{aligned} \end{align*} $$

From Lemma 3.5 and the trivial bounds of $G(\alpha _i)$ and $T(\alpha _{i}, V_{i})$ ,

(4.2) $$ \begin{align} \kern-10pt\begin{aligned} R_{2}(N_{1}, N_{2}) &=\iint_{C(\mathfrak{M}) \cap \mathscr{E}_{\lambda}}S^{4}(\alpha_{1}, U_{1})T^{4}(\alpha_{1}, V_{1})S^{4}(\alpha_{2},U_{2})T^{4}(\alpha_{2}, V_{2}) \\&\qquad \times G^{k}(\alpha_{1}+\alpha_{2}) e(-\alpha_{1} N_{1}-\alpha_{2} N_{2}) \,{d} \alpha_{1} \,{d} \alpha_{2}\\&\ll L^{k}\bigg(\iint_{\substack{(\alpha_{1}, \alpha_{2}) \in C(\mathfrak{M}_{1}) \times[0,1] \\ |G(\alpha_{1}+\alpha_{2})| \geq \lambda L}}+\iint_{\substack{(\alpha_{1}, \alpha_{2}) \in[0,1] \times C(\mathfrak{M}_{2}) \\ |G(\alpha_{1}+\alpha_{2})| \geq \lambda L}}\bigg)\\&\qquad S^{4}(\alpha_{1}, U_{1})T^{4}(\alpha_{1}, V_{1})S^{4}(\alpha_{2},U_{2})T^{4}(\alpha_{2}, V_{2})\,{d} \alpha_{1} \,{d} \alpha_{2} \\&\ll L^{k} N_{1}^{{10}/{9}}N_{1}^{{11}/{9}+\epsilon} \iint_{\substack{(\alpha_{1}, \alpha_{2}) \in[0,1]^{2} \\ |G(\alpha_{1}+\alpha_{2})| \geq\lambda L}}|S^{4}(\alpha_{2},U_{2})T^{4}(\alpha_{2}, V_{2})| \,{d} \alpha_{1} \,{d} \alpha_{2} \\&\qquad +L^{k} N_{2}^{{10}/{9}}N_{2}^{{11}/{9}+\epsilon} \iint_{\substack{(\alpha_{1}, \alpha_{2}) \in[0,1]^{2} \\ |G(\alpha_{1}+\alpha_{2})| \geq \lambda L}}|S^{4}(\alpha_{1},U_{1})T^{4}(\alpha_{1}, V_{1})| \,{d} \alpha_{1} \,{d} \alpha_{2}. \end{aligned} \end{align} $$

Let $\varpi =\alpha _{1}+\alpha _{2}$ . By the periodicity of $G(\alpha )$ ,

$$ \begin{align*} \begin{split} \iint_{\substack{(\alpha_{1}, \alpha_{2}) \in[0,1]^{2} \\ |G(\alpha_{1}+\alpha_{2})| \geq \lambda L}} &|S^{4}(\alpha_{2},U_{2})T^{4}(\alpha_{2}, V_{2})| \,{d} \alpha_{1} \,{d} \alpha_{2}\\ &=\int_{0}^{1}|S^{4}(\alpha_{2},U_{2})T^{4}(\alpha_{2}, V_{2})|\bigg(\int_{\substack{\varpi \in[\alpha_{2}, 1+\alpha_{2}] \\|G(\varpi)| \geq \lambda L}} \,{d} \varpi\bigg) \,{d} \alpha_{2}. \end{split} \end{align*} $$

By Lemmas 3.4 and 3.6,

(4.3) $$ \begin{align} \iint_{\substack{(\alpha_{1}, \alpha_{2}) \in[0,1]^{2} \\|G(\alpha_{1}+\alpha_{2})| \geq \lambda L}}|S^{4}(\alpha_{2},U_{2})T^{4}(\alpha_{2}, V_{2})| \,{d} \alpha_{1} \,{d} \alpha_{2} \ll N_{2}^{{13}/{9}}N_{1}^{-{8}/{9}-10^{-10}}. \end{align} $$

Similarly,

(4.4) $$ \begin{align} \iint_{\substack{(\alpha_{1}, \alpha_{2}) \in[0,1]^{2} \\|G(\alpha_{1}+\alpha_{2})| \geq \lambda L}}|S^{4}(\alpha_{1},U_{1})T^{4}(\alpha_{1}, V_{1})| \,{d} \alpha_{1} \,{d} \alpha_{2} \ll N_{1}^{{13}/{9}}N_{2}^{-{8}/{9}-10^{-10}}. \end{align} $$

From (4.2)–(4.4),

(4.5) $$ \begin{align} R_{2}(N_{1},N_{2})&\ll N_{1}^{{10}/{9}}N_{1}^{{11}/{9}+\epsilon}N_{2}^{{13}/{9}}N_{1}^{-{8}/{9}-10^{-10}}L^{k}+ N_{2}^{{10}/{9}}N_{2}^{{11}/{9}+\epsilon}N_{1}^{{13}/{9}}N_{2}^{-{8}/{9}-10^{-10}}L^{k} \nonumber\\ &\ll (N_{1}N_{2})^{{13}/{9}}L^{k-1}, \end{align} $$

where $N_{2}\gg N_{1}>N_{2}$ .

Finally, we estimate $R_{3}(N_{1},N_{2})$ . By Lemma 3.6 and the definition of $\mathscr {E}_{\lambda }$ ,

(4.6) $$ \begin{align} \begin{aligned} R_{3}& (N_{1}, N_{2}) \\ & = \iint_{C(\mathfrak{M}) \backslash \mathscr{E}_{\lambda}}S^{4}(\alpha_{1}, U_{1})T^{4}(\alpha_{1}, V_{1})S^{4}(\alpha_{2},U_{2})T^{4}(\alpha_{2}, V_{2}) \\ &\quad \times G^{k}(\alpha_{1}+\alpha_{2}) e(-\alpha_{1} N_{1}-\alpha_{2} N_{2}) \,{d} \alpha_{1} \,{d} \alpha_{2} \\ & \leq(\lambda L)^{k} \int_{0}^{1} |S^{4}(\alpha_{1},U_{1}) T^{4}(\alpha_{1},V_{1})| \,{d} \alpha_{1}\int_{0}^{1} |S^{4}(\alpha_{2},U_{2}) T^{4}(\alpha_{2},V_{2})| \,{d} \alpha_{2} \\ & \leq 0.0181424982 \lambda^{k}(N_{1} N_{2})^{{13}/{9}} L^{k}. \end{aligned} \end{align} $$

Putting (4.1), (4.5) and (4.6) together,

$$ \begin{align*} \begin{aligned} R(N_{1}, N_{2})&>R_{1}(N_{1}, N_{2})-R_{3}(N_{1}, N_{2})+O((N_{1} N_{2})^{{13}/{9}} L^{k-1}) \\ &>(7.524395606\times10^{-9}-0.0181424982\lambda^{k})(N_{1} N_{2})^{{13}/{9}} L^{k}, \end{aligned} \end{align*} $$

where $\lambda =0.9570253$ . Then we can deduce that

$$ \begin{align*}R(N_{1}, N_{2})>0\end{align*} $$

provided that $k\geq 335$ . Thus, we complete the proof of Theorem 1.1.