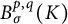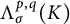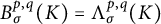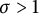1 Introduction
In this paper, we study the identity of two classes of Besov spaces on post-critically finite (p.c.f.) self-similar sets with regular harmonic structure. One class is the heat Besov spaces
![]() $B^{p,q}_\sigma (K)$
, defined with the Neumann Laplacian
$B^{p,q}_\sigma (K)$
, defined with the Neumann Laplacian
![]() $\Delta _N$
, which was introduced in the study of Brownian motions on self-similar sets (see [Reference Barlow and Bass5–Reference Barlow and Perkins7, Reference Goldstein16, Reference Kusuoka and Zhou30, Reference Lindstrøm31]), and was later extended to general p.c.f. self-similar sets in a purely analytical way by Kigami [Reference Kigami24, Reference Kigami25]. The heat Besov spaces
$\Delta _N$
, which was introduced in the study of Brownian motions on self-similar sets (see [Reference Barlow and Bass5–Reference Barlow and Perkins7, Reference Goldstein16, Reference Kusuoka and Zhou30, Reference Lindstrøm31]), and was later extended to general p.c.f. self-similar sets in a purely analytical way by Kigami [Reference Kigami24, Reference Kigami25]. The heat Besov spaces
![]() $B^{p,q}_\sigma (K)$
are defined as potential spaces following [Reference Hu and Zähle23],
$B^{p,q}_\sigma (K)$
are defined as potential spaces following [Reference Hu and Zähle23],
 $$\begin{align*}B^{p,q}_\sigma(K)=\left\{f\in L^p(K):\left(\int_{0}^\infty \left(t^{-\sigma/2}\left\|(t\Delta_N)^kP_tf\right\|_{L^p(K)}\right)^{q}dt/t\right)^{1/q}<\infty\right\}, \end{align*}$$
$$\begin{align*}B^{p,q}_\sigma(K)=\left\{f\in L^p(K):\left(\int_{0}^\infty \left(t^{-\sigma/2}\left\|(t\Delta_N)^kP_tf\right\|_{L^p(K)}\right)^{q}dt/t\right)^{1/q}<\infty\right\}, \end{align*}$$
where
![]() $\{P_t\}_{t\geq 0}$
is the heat semigroup associated with
$\{P_t\}_{t\geq 0}$
is the heat semigroup associated with
![]() $\Delta _N$
. Here, we take the measure
$\Delta _N$
. Here, we take the measure
![]() $\mu $
to be self-similar and
$\mu $
to be self-similar and
![]() $d_H$
-regular with respect to the effective resistance metric
$d_H$
-regular with respect to the effective resistance metric
![]() $R(\cdot ,\cdot )$
on K, where
$R(\cdot ,\cdot )$
on K, where
![]() $d_H$
is the Hausdorff dimension of K under R. The other class
$d_H$
is the Hausdorff dimension of K under R. The other class
![]() $\Lambda ^{p,q}_\sigma (K)$
, named Lipschitz–Besov spaces, is defined in terms of difference of functions
$\Lambda ^{p,q}_\sigma (K)$
, named Lipschitz–Besov spaces, is defined in terms of difference of functions
 $$\begin{align*}\Lambda^{p,q}_\sigma(K)=\left\{f\in L^p(K):\left(\!\int_0^\infty\!\left(\!\int_Kt^{-d_H}\!\int_{B_t(x)}\!\frac{|f(x)-f(y)|^p}{t^{\sigma pd_W /2}}d\mu(y)d\mu(x)\right)^{q/p}\frac{dt}{t}\right)^{1/q}\!<\infty\right\} \end{align*}$$
$$\begin{align*}\Lambda^{p,q}_\sigma(K)=\left\{f\in L^p(K):\left(\!\int_0^\infty\!\left(\!\int_Kt^{-d_H}\!\int_{B_t(x)}\!\frac{|f(x)-f(y)|^p}{t^{\sigma pd_W /2}}d\mu(y)d\mu(x)\right)^{q/p}\frac{dt}{t}\right)^{1/q}\!<\infty\right\} \end{align*}$$
for
![]() $1\leq q<\infty $
, and
$1\leq q<\infty $
, and
 $$\begin{align*}\Lambda^{p,\infty}_\sigma(K)=\left\{f\in L^p(K):\sup_{t>0} \left(\int_Kt^{-d_H}\int_{B_t(x)}\frac{|f(x)-f(y)|^p}{t^{\sigma pd_W /2}}d\mu(y)d\mu(x)\right)<\infty\right\}, \end{align*}$$
$$\begin{align*}\Lambda^{p,\infty}_\sigma(K)=\left\{f\in L^p(K):\sup_{t>0} \left(\int_Kt^{-d_H}\int_{B_t(x)}\frac{|f(x)-f(y)|^p}{t^{\sigma pd_W /2}}d\mu(y)d\mu(x)\right)<\infty\right\}, \end{align*}$$
where
![]() $B_t(x)$
is the ball of radius t centered at x under the metric R, and
$B_t(x)$
is the ball of radius t centered at x under the metric R, and
![]() $d_W=1+d_H$
is the walk dimension of the associated heat kernel. Roughly speaking,
$d_W=1+d_H$
is the walk dimension of the associated heat kernel. Roughly speaking,
![]() $d_H$
reflects the growth of the measure, and
$d_H$
reflects the growth of the measure, and
![]() $d_W$
reflects the speed of the diffusion process. There is another exponent
$d_W$
reflects the speed of the diffusion process. There is another exponent
![]() $d_S$
that will be involved in the study of
$d_S$
that will be involved in the study of
![]() $B_\sigma ^{p,q}(K)$
and
$B_\sigma ^{p,q}(K)$
and
![]() $\Lambda _{\sigma }^{p,q}(K)$
, called the spectral dimension. It is known that
$\Lambda _{\sigma }^{p,q}(K)$
, called the spectral dimension. It is known that
![]() $d_S=\frac {2d_H}{d_W}$
and it reflects the asymptotical law of the eigenvalue counting function associate with
$d_S=\frac {2d_H}{d_W}$
and it reflects the asymptotical law of the eigenvalue counting function associate with
![]() $\Delta _N$
(see [Reference Kigami26, Reference Kigami and Lapidus28]). More explanations on general metric measure spaces can be found in [Reference Grigor'Yan, Hu and Lau18].
$\Delta _N$
(see [Reference Kigami26, Reference Kigami and Lapidus28]). More explanations on general metric measure spaces can be found in [Reference Grigor'Yan, Hu and Lau18].
The relationship between the two classes of Besov spaces
![]() $B^{p,q}_\sigma (K)$
and
$B^{p,q}_\sigma (K)$
and
![]() $\Lambda ^{p,q}_\sigma (K)$
has been a long-term problem [Reference Pietruska-Pałuba32] on general metric measure spaces, and whether the identity
$\Lambda ^{p,q}_\sigma (K)$
has been a long-term problem [Reference Pietruska-Pałuba32] on general metric measure spaces, and whether the identity
holds is of particular interest. For
![]() $p=q=2$
and
$p=q=2$
and
![]() $0<\sigma <1$
, when the Besov spaces coincide with the Sobolev spaces, under some weak assumption of heat kernel estimates, Hu and Zähle [Reference Hu and Zähle23] showed that (1.1) holds, as well as Strichartz [Reference Strichartz35] obtained the same result on products of p.c.f. self-similar sets at the same time. Later, Grigor’yan and Liu proved that (1.1) holds for any
$0<\sigma <1$
, when the Besov spaces coincide with the Sobolev spaces, under some weak assumption of heat kernel estimates, Hu and Zähle [Reference Hu and Zähle23] showed that (1.1) holds, as well as Strichartz [Reference Strichartz35] obtained the same result on products of p.c.f. self-similar sets at the same time. Later, Grigor’yan and Liu proved that (1.1) holds for any
![]() $1<p,q<\infty $
and any
$1<p,q<\infty $
and any
![]() $0<\sigma <\frac {2\Theta }{d_W}\wedge 1$
, where
$0<\sigma <\frac {2\Theta }{d_W}\wedge 1$
, where
![]() $\Theta $
denotes the Hölder exponent of the heat kernel (see [Reference Grigor'yan and Liu19]). Note that on p.c.f. self-similar sets, due to the sub-Gaussian heat kernel estimates (see [Reference Hambly and Kumagai21, Reference Kumagai and Sturm29]), the existence of small Hölder exponent
$\Theta $
denotes the Hölder exponent of the heat kernel (see [Reference Grigor'yan and Liu19]). Note that on p.c.f. self-similar sets, due to the sub-Gaussian heat kernel estimates (see [Reference Hambly and Kumagai21, Reference Kumagai and Sturm29]), the existence of small Hölder exponent
![]() $\Theta $
was shown in [Reference Grigor'Yan, Hu and Lau18]. Until now, a larger region where (1.1) holds or not is still hard to reach.
$\Theta $
was shown in [Reference Grigor'Yan, Hu and Lau18]. Until now, a larger region where (1.1) holds or not is still hard to reach.
Recently, Cao and Grigor’yan made much progress on this problem (see [Reference Cao and Grigor’yan10, Reference Cao and Grigor’yan11]). They showed that (1.1) holds on a larger region, under the assumption of Gaussian heat kernel estimates. Their work utilizes some new techniques, but the results and ideas are restricted to the
![]() $d_W=2$
case. For the general
$d_W=2$
case. For the general
![]() $d_W>2$
case, the study is still on going.
$d_W>2$
case, the study is still on going.
In this paper, we will focus on p.c.f. self-similar sets with regular harmonic structures, which are a class of well-known fractals where sub-Gaussian heat kernel estimates hold. In particular, we will describe a sharp region where (1.1) holds. See the left panel of Figure 1.

Figure 1: The sharp region for (1.1) and the possible area where
![]() $\mathscr {C}$
lies.
$\mathscr {C}$
lies.
More precisely, we introduce a critical curve
![]() $\mathscr {C}$
, for
$\mathscr {C}$
, for
![]() $1\leq p\leq \infty $
,
$1\leq p\leq \infty $
,
where
![]() $\mathcal {H}_0$
is the space of harmonic functions. Our main result in this paper is the following theorem.
$\mathcal {H}_0$
is the space of harmonic functions. Our main result in this paper is the following theorem.
Theorem 1.1 For
![]() $1<p<\infty $
,
$1<p<\infty $
,
![]() $1\leq q\leq \infty $
and
$1\leq q\leq \infty $
and
![]() $0<\sigma <\mathscr {C}(p)$
, we have
$0<\sigma <\mathscr {C}(p)$
, we have
![]() $B^{p,q}_\sigma (K)=\Lambda ^{p,q}_\sigma (K)$
, and their norms are equivalent. In addition,
$B^{p,q}_\sigma (K)=\Lambda ^{p,q}_\sigma (K)$
, and their norms are equivalent. In addition,
One important fact about the theorem is that the identical region of (1.1) is sharp. Indeed, it is not hard to see that
We will explain this in Proposition 3.2 at the beginning of Section 3.
One may compare
![]() $\mathscr {C}(p)$
with another important critical exponent
$\mathscr {C}(p)$
with another important critical exponent
Though, for
![]() $p=2$
, we always have
$p=2$
, we always have
![]() $\sigma ^\#_2=1=\mathscr {C}(2)$
[Reference Grigor'Yan, Hu and Lau18], we have to say that
$\sigma ^\#_2=1=\mathscr {C}(2)$
[Reference Grigor'Yan, Hu and Lau18], we have to say that
![]() $\sigma ^\#_p$
is not in general equal to
$\sigma ^\#_p$
is not in general equal to
![]() $\mathscr {C}(p)$
. In fact, it has been shown that
$\mathscr {C}(p)$
. In fact, it has been shown that
![]() $\sigma ^\#_1=d_S$
in [Reference Alonso-Ruiz, Baudoin, Chen, Rogers, Shanmugalingam and Teplyaev4] for nested fractals, while on the Sierpinski gasket,
$\sigma ^\#_1=d_S$
in [Reference Alonso-Ruiz, Baudoin, Chen, Rogers, Shanmugalingam and Teplyaev4] for nested fractals, while on the Sierpinski gasket,
![]() $\mathscr {C}(1)<d_S$
is indicated by Theorems 5.1 and 5.2 of [Reference Alonso-Ruiz, Baudoin, Chen, Rogers, Shanmugalingam and Teplyaev4] (also see Example 3 in Section 3 for a rough estimate by a simple calculation).
$\mathscr {C}(1)<d_S$
is indicated by Theorems 5.1 and 5.2 of [Reference Alonso-Ruiz, Baudoin, Chen, Rogers, Shanmugalingam and Teplyaev4] (also see Example 3 in Section 3 for a rough estimate by a simple calculation).
It is not hard to find a narrow region where
![]() $\mathscr {C}$
lives, see the right panel of Figure 1 for an illustration. Although much information of
$\mathscr {C}$
lives, see the right panel of Figure 1 for an illustration. Although much information of
![]() $\mathscr {C}$
can be derived with Proposition 5.6 in [Reference Alonso-Ruiz, Baudoin, Chen, Rogers, Shanmugalingam and Teplyaev2] and Theorem 3.11 in [Reference Alonso-Ruiz, Baudoin, Chen, Rogers, Shanmugalingam and Teplyaev4], to provide an intuitive understanding of Theorem 1.1, and to make our exposition self-contained, we will provide a short, elementary discussion on
$\mathscr {C}$
can be derived with Proposition 5.6 in [Reference Alonso-Ruiz, Baudoin, Chen, Rogers, Shanmugalingam and Teplyaev2] and Theorem 3.11 in [Reference Alonso-Ruiz, Baudoin, Chen, Rogers, Shanmugalingam and Teplyaev4], to provide an intuitive understanding of Theorem 1.1, and to make our exposition self-contained, we will provide a short, elementary discussion on
![]() $\mathscr {C}$
in Section 3 (see Proposition 3.3). Write
$\mathscr {C}$
in Section 3 (see Proposition 3.3). Write
with
![]() $p'=\frac {p}{p-1}$
.
$p'=\frac {p}{p-1}$
.
![]() $\mathscr {L}_1$
is naturally the critical line concerning the continuity of functions, and
$\mathscr {L}_1$
is naturally the critical line concerning the continuity of functions, and
![]() $\mathscr {L}_2$
is the critical line concerning the Hölder continuity of functions and thus the existence of normal derivatives at boundaries. In the authors’ related works [Reference Cao and Qiu12–Reference Cao and Qiu14], there is a discussion on the role of these critical lines concerning the relationship between Sobolev spaces and (heat) Besov spaces on p.c.f. self-similar sets with different boundary conditions. We will see that the curve
$\mathscr {L}_2$
is the critical line concerning the Hölder continuity of functions and thus the existence of normal derivatives at boundaries. In the authors’ related works [Reference Cao and Qiu12–Reference Cao and Qiu14], there is a discussion on the role of these critical lines concerning the relationship between Sobolev spaces and (heat) Besov spaces on p.c.f. self-similar sets with different boundary conditions. We will see that the curve
![]() $\mathscr C$
is concave and increasing w.r.t.
$\mathscr C$
is concave and increasing w.r.t.
![]() $\frac 1 p$
, and in addition:
$\frac 1 p$
, and in addition:
(1). for
![]() $1\leq p\leq 2$
,
$1\leq p\leq 2$
,
![]() $1\leq \mathscr {C}(p)\leq \frac {2}{d_W}+\frac {2}{p}\cdot \frac {d_H-1}{d_W}$
,
$1\leq \mathscr {C}(p)\leq \frac {2}{d_W}+\frac {2}{p}\cdot \frac {d_H-1}{d_W}$
,
(2). for
![]() $2\leq p\leq \infty $
,
$2\leq p\leq \infty $
,
![]() $\frac {2}{d_W}+\frac {2}{p}\cdot \frac {d_H-1}{d_W}\leq \mathscr {C}(p)\leq 1\wedge \mathscr {L}_2(p)$
.
$\frac {2}{d_W}+\frac {2}{p}\cdot \frac {d_H-1}{d_W}\leq \mathscr {C}(p)\leq 1\wedge \mathscr {L}_2(p)$
.
See the right panel of Figure 1. In particular, it may happen that
![]() $\mathscr {C}(1)>1$
(for example, it is true for the Vicsek set and the Sierpinski gasket in standard setting), so (1.1) even holds in some cases when
$\mathscr {C}(1)>1$
(for example, it is true for the Vicsek set and the Sierpinski gasket in standard setting), so (1.1) even holds in some cases when
![]() $\sigma>1$
. This is a surprising result which was not mentioned in previous studies.
$\sigma>1$
. This is a surprising result which was not mentioned in previous studies.
The exact characterization of the critical curve
![]() $\mathscr {C}$
, and the problem of whether the identity (1.1) holds along
$\mathscr {C}$
, and the problem of whether the identity (1.1) holds along
![]() $\mathscr {C}$
, are still out of reach, and are left to the future study. It is of particular interest to see whether
$\mathscr {C}$
, are still out of reach, and are left to the future study. It is of particular interest to see whether
![]() $\mathscr {C}(1)>1$
always holds when
$\mathscr {C}(1)>1$
always holds when
![]() $d_W>2$
. Despite of this, we are able to fully describe the curve
$d_W>2$
. Despite of this, we are able to fully describe the curve
![]() $\mathscr {C}$
for the class of Vicsek sets (see Example 2 in Section 3).
$\mathscr {C}$
for the class of Vicsek sets (see Example 2 in Section 3).
At the end of this section, we mention that, due to the nested structure of p.c.f. self-similar sets, discrete characterizations of function spaces play natural and essential role throughout our study. This might also be a proper starting point for problems on general metric measure spaces by involving suitable partitions (see [Reference Kigami27]).
Now, we briefly introduce the structure of this paper. Section 2 will serve as the background of this paper, where we introduce necessary knowledge and notations, including the p.c.f. self-similar sets, the Dirichlet forms and Laplacians on fractals, and the definitions of function spaces we consider here. In Section 3, we will discuss the critical curve
![]() $\mathscr {C}$
and provide several examples. This will help readers to understand the sharp region in the main theorem. In Section 4, we focus on the Lipschitz–Besov spaces
$\mathscr {C}$
and provide several examples. This will help readers to understand the sharp region in the main theorem. In Section 4, we focus on the Lipschitz–Besov spaces
![]() $\Lambda ^{p,q}_\sigma (K)$
. We will provide two kinds of discrete type characterizations of
$\Lambda ^{p,q}_\sigma (K)$
. We will provide two kinds of discrete type characterizations of
![]() $\Lambda ^{p,q}_\sigma (K)$
, which will serve as a main tool toward the main theorem. In Sections 5 and 6, we prove the main theorem, Theorem 1.1. In particular, we will show that
$\Lambda ^{p,q}_\sigma (K)$
, which will serve as a main tool toward the main theorem. In Sections 5 and 6, we prove the main theorem, Theorem 1.1. In particular, we will show that
![]() $\Lambda ^{p,q}_\sigma (K)\subset B^{p,q}_\sigma (K)$
for any
$\Lambda ^{p,q}_\sigma (K)\subset B^{p,q}_\sigma (K)$
for any
![]() $1<p<\infty $
,
$1<p<\infty $
,
![]() $1\leq q\leq \infty $
and
$1\leq q\leq \infty $
and
![]() $0<\sigma <2$
in Section 5. In Section 6, we will prove the other direction, i.e.,
$0<\sigma <2$
in Section 5. In Section 6, we will prove the other direction, i.e.,
![]() $B^{p,q}_\sigma (K)\subset \Lambda ^{p,q}_\sigma (K)$
with
$B^{p,q}_\sigma (K)\subset \Lambda ^{p,q}_\sigma (K)$
with
![]() $1<p<\infty $
,
$1<p<\infty $
,
![]() $1\leq q\leq \infty $
and
$1\leq q\leq \infty $
and
![]() $0<\sigma <\mathscr {C}(p)$
.
$0<\sigma <\mathscr {C}(p)$
.
Throughout the paper, we will always write
![]() $f\lesssim g$
if there is a constant
$f\lesssim g$
if there is a constant
![]() $C>0$
such that
$C>0$
such that
![]() $f\leq C g$
when we do not emphasize the constant C. In addition, we write
$f\leq C g$
when we do not emphasize the constant C. In addition, we write
![]() $f\asymp g$
if both
$f\asymp g$
if both
![]() $f\lesssim g$
and
$f\lesssim g$
and
![]() $g\lesssim f$
hold.
$g\lesssim f$
hold.
2 Preliminary
The analysis on p.c.f. self-similar sets was originally developed by Kigami in [Reference Kigami25, Reference Kigami26]. For convenience of readers, in this section, first, we will briefly recall the constructions of Dirichlet forms and Laplacians on p.c.f. fractals. We refer to books [Reference Kigami26, Reference Strichartz36] for details. Then we will provide the definitions of the two classes of Besov spaces,
![]() $B^{p,q}_\sigma (K)$
and
$B^{p,q}_\sigma (K)$
and
![]() $\Lambda ^{p,q}_\sigma (K)$
. There is a large literature on function spaces on fractals or on more general metric measure spaces (see [Reference Alonso-Ruiz, Baudoin, Chen, Rogers, Shanmugalingam and Teplyaev2–Reference Alonso-Ruiz, Baudoin, Chen, Rogers, Shanmugalingam and Teplyaev4, Reference Cao and Qiu12–Reference Gogatishvili, Koskela and Shanmugalingam15, Reference Grigor’yan17, Reference Hinz, Koch and Meinert22, Reference Strichartz34] and the references therein).
$\Lambda ^{p,q}_\sigma (K)$
. There is a large literature on function spaces on fractals or on more general metric measure spaces (see [Reference Alonso-Ruiz, Baudoin, Chen, Rogers, Shanmugalingam and Teplyaev2–Reference Alonso-Ruiz, Baudoin, Chen, Rogers, Shanmugalingam and Teplyaev4, Reference Cao and Qiu12–Reference Gogatishvili, Koskela and Shanmugalingam15, Reference Grigor’yan17, Reference Hinz, Koch and Meinert22, Reference Strichartz34] and the references therein).
Let
![]() $\{F_i\}_{i=1}^N$
be a finite collection of contractions on a complete metric space
$\{F_i\}_{i=1}^N$
be a finite collection of contractions on a complete metric space
![]() $(\mathcal M,d)$
. The self-similar set associated with the iterated function system (i.f.s.)
$(\mathcal M,d)$
. The self-similar set associated with the iterated function system (i.f.s.)
![]() $\{F_i\}_{i=1}^N$
is the unique compact set
$\{F_i\}_{i=1}^N$
is the unique compact set
![]() $K\subset \mathcal M$
satisfying
$K\subset \mathcal M$
satisfying
 $$\begin{align*}K=\bigcup_{i=1}^N F_iK.\end{align*}$$
$$\begin{align*}K=\bigcup_{i=1}^N F_iK.\end{align*}$$
For
![]() $m\geq 1$
, we define
$m\geq 1$
, we define
![]() $W_m=\{1,\ldots ,N\}^m$
the collection of words of length m, and for each
$W_m=\{1,\ldots ,N\}^m$
the collection of words of length m, and for each
![]() $w\in W_m$
, denote
$w\in W_m$
, denote
Set
![]() $W_0=\emptyset $
, and let
$W_0=\emptyset $
, and let
![]() $W_*=\bigcup _{m\geq 0} W_m$
be the collection of all finite words. For
$W_*=\bigcup _{m\geq 0} W_m$
be the collection of all finite words. For
![]() $w=w_1w_2\ldots w_m\in W_*\setminus W_0$
, we write
$w=w_1w_2\ldots w_m\in W_*\setminus W_0$
, we write
![]() $w^*=w_1w_2\ldots w_{m-1}$
by deleting the last letter of w.
$w^*=w_1w_2\ldots w_{m-1}$
by deleting the last letter of w.
Define the shift space
![]() $\Sigma =\{1,2,\ldots ,N\}^{\mathbb {N}}$
. There is a continuous surjection
$\Sigma =\{1,2,\ldots ,N\}^{\mathbb {N}}$
. There is a continuous surjection
![]() $\pi : \Sigma \rightarrow K$
defined by
$\pi : \Sigma \rightarrow K$
defined by
where for
![]() $\omega =\omega _1\omega _2\ldots $
in
$\omega =\omega _1\omega _2\ldots $
in
![]() $\Sigma $
we write
$\Sigma $
we write
![]() $[\omega ]_m=\omega _1\omega _2\ldots \omega _m\in W_m$
for each
$[\omega ]_m=\omega _1\omega _2\ldots \omega _m\in W_m$
for each
![]() $m\geq 1$
. Let
$m\geq 1$
. Let
where
![]() $\sigma $
is the shift map define as
$\sigma $
is the shift map define as
![]() $\sigma (\omega _1\omega _2\ldots )=\omega _2\omega _3\ldots $
.
$\sigma (\omega _1\omega _2\ldots )=\omega _2\omega _3\ldots $
.
![]() $\mathcal {P}$
is called the post-critical set. Call K a p.c.f. self-similar set if
$\mathcal {P}$
is called the post-critical set. Call K a p.c.f. self-similar set if
![]() $\#\mathcal {P}<\infty $
. In what follows, we always assume that K is a connected p.c.f. self-similar set.
$\#\mathcal {P}<\infty $
. In what follows, we always assume that K is a connected p.c.f. self-similar set.
Let
![]() $V_0=\pi (\mathcal {P})$
and call it the boundary of K. For
$V_0=\pi (\mathcal {P})$
and call it the boundary of K. For
![]() $m\geq 1$
, we always have
$m\geq 1$
, we always have
![]() $F_w K\cap F_{w'}K\subset F_w V_0\cap F_{w'}V_0$
for any
$F_w K\cap F_{w'}K\subset F_w V_0\cap F_{w'}V_0$
for any
![]() $w\neq w'\in W_m$
. Denote
$w\neq w'\in W_m$
. Denote
![]() $V_m=\bigcup _{w\in W_m}F_wV_0$
, and let
$V_m=\bigcup _{w\in W_m}F_wV_0$
, and let
![]() $l(V_m)=\{f: f \text { maps } V_m \text { into } \mathbb {C}\}$
. Write
$l(V_m)=\{f: f \text { maps } V_m \text { into } \mathbb {C}\}$
. Write
![]() $V_*=\bigcup _{m\geq 0}V_m$
.
$V_*=\bigcup _{m\geq 0}V_m$
.
Let
![]() $H=(H_{pq})_{p,q\in V_0}$
be a symmetric linear operator(matrix). H is called a (discrete) Laplacian on
$H=(H_{pq})_{p,q\in V_0}$
be a symmetric linear operator(matrix). H is called a (discrete) Laplacian on
![]() $V_0$
if H is nonpositive definite;
$V_0$
if H is nonpositive definite;
![]() $Hu=0$
if and only if u is constant on
$Hu=0$
if and only if u is constant on
![]() $V_0$
; and
$V_0$
; and
![]() $H_{pq}\geq 0$
for any
$H_{pq}\geq 0$
for any
![]() $p\neq q\in V_0$
. Given a Laplacian H on
$p\neq q\in V_0$
. Given a Laplacian H on
![]() $V_0$
and a vector
$V_0$
and a vector
![]() $\boldsymbol {r}=\{r_i\}_{i=1}^N$
with
$\boldsymbol {r}=\{r_i\}_{i=1}^N$
with
![]() $r_i>0$
,
$r_i>0$
,
![]() $1\leq i\leq N$
, define the (discrete) energy form on
$1\leq i\leq N$
, define the (discrete) energy form on
![]() $V_0$
by
$V_0$
by
and inductively on
![]() $V_m$
by
$V_m$
by
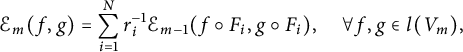 $$ \begin{align*}\mathcal{E}_m(f,g)=\sum_{i=1}^Nr^{-1}_i\mathcal{E}_{m-1}(f\circ F_i, g\circ F_i), \quad \forall f,g\in l(V_m),\end{align*} $$
$$ \begin{align*}\mathcal{E}_m(f,g)=\sum_{i=1}^Nr^{-1}_i\mathcal{E}_{m-1}(f\circ F_i, g\circ F_i), \quad \forall f,g\in l(V_m),\end{align*} $$
for
![]() $m\geq 1$
. Write
$m\geq 1$
. Write
![]() $\mathcal {E}_m(f,f)=\mathcal {E}_m(f)$
for short.
$\mathcal {E}_m(f,f)=\mathcal {E}_m(f)$
for short.
Say
![]() $(H,\boldsymbol {r})$
is a harmonic structure if for any
$(H,\boldsymbol {r})$
is a harmonic structure if for any
![]() $f\in l(V_0)$
,
$f\in l(V_0)$
,
In this paper, we will always assume that there exists a harmonic structure associated with K, and in addition,
![]() $0<r_i<1$
for all
$0<r_i<1$
for all
![]() $1\leq i\leq N$
. Call
$1\leq i\leq N$
. Call
![]() $(H,\boldsymbol {r})$
a regular harmonic structure on K. It is known that the question of when a p.c.f. self-similar set admits a regular harmonic structure is nontrivial, for example, see [Reference Kigami26, Section 3.1].
$(H,\boldsymbol {r})$
a regular harmonic structure on K. It is known that the question of when a p.c.f. self-similar set admits a regular harmonic structure is nontrivial, for example, see [Reference Kigami26, Section 3.1].
Now, for each
![]() $f\in C(K)$
, the sequence
$f\in C(K)$
, the sequence
![]() $\{\mathcal {E}_m(f)\}_{m\geq 0}$
is nondecreasing. Let
$\{\mathcal {E}_m(f)\}_{m\geq 0}$
is nondecreasing. Let
where
![]() $f,g\in C(K)$
and we write
$f,g\in C(K)$
and we write
![]() $\mathcal {E}(f):=\mathcal {E}(f,f)$
for short. Call
$\mathcal {E}(f):=\mathcal {E}(f,f)$
for short. Call
![]() $\mathcal {E}(f)$
the energy of f. It is known that
$\mathcal {E}(f)$
the energy of f. It is known that
![]() $(\mathcal {E},dom\mathcal {E})$
turns out to be a local regular Dirichlet form on
$(\mathcal {E},dom\mathcal {E})$
turns out to be a local regular Dirichlet form on
![]() $L^2(K,\mu )$
for any Radon measure
$L^2(K,\mu )$
for any Radon measure
![]() $\mu $
on K.
$\mu $
on K.
An important feature of the form
![]() $(\mathcal {E},dom\mathcal {E})$
is the self-similar identity,
$(\mathcal {E},dom\mathcal {E})$
is the self-similar identity,
 $$ \begin{align} \mathcal{E}(f,g)=\sum_{i=1}^Nr_i^{-1}\mathcal{E}(f\circ F_i, g\circ F_i), \quad \forall f,g\in dom\mathcal{E}. \end{align} $$
$$ \begin{align} \mathcal{E}(f,g)=\sum_{i=1}^Nr_i^{-1}\mathcal{E}(f\circ F_i, g\circ F_i), \quad \forall f,g\in dom\mathcal{E}. \end{align} $$
Furthermore, denote
![]() $r_w=r_{w_1}r_{w_2}\ldots r_{w_m}$
for each
$r_w=r_{w_1}r_{w_2}\ldots r_{w_m}$
for each
![]() $w\in W_m, m\geq 0$
. Then, for
$w\in W_m, m\geq 0$
. Then, for
![]() $m\geq 1$
, we have
$m\geq 1$
, we have
2.1 The Laplacian and harmonic functions
To study the Besov spaces on K, we need a suitable metric and a comparable measure. Instead of the original metric d, a natural choice of metric is the effective resistance metric
![]() $R(\cdot ,\cdot )$
[Reference Kigami26], which matches the form
$R(\cdot ,\cdot )$
[Reference Kigami26], which matches the form
![]() $(\mathcal {E},dom{\mathcal {E}})$
.
$(\mathcal {E},dom{\mathcal {E}})$
.
Definition 2.1 For
![]() $x,y\in K$
, the effective resistance metric
$x,y\in K$
, the effective resistance metric
![]() $R(x,y)$
between x and y is defined by
$R(x,y)$
between x and y is defined by
It is known that R is indeed a metric on K which is topologically equivalent to the metric d, and for each
![]() $w\in W_*$
, we always have
$w\in W_*$
, we always have
![]() $diam(F_wK)\asymp r_w$
, where
$diam(F_wK)\asymp r_w$
, where
![]() $diam(F_wK)=\max \left \{R(x,y):x,y\in F_wK\right \}$
. For convenience, we normalize
$diam(F_wK)=\max \left \{R(x,y):x,y\in F_wK\right \}$
. For convenience, we normalize
![]() $diam K$
to be
$diam K$
to be
![]() $1$
and so that we additionally have
$1$
and so that we additionally have
![]() $diam (F_wK)\leq r_w$
,
$diam (F_wK)\leq r_w$
,
![]() $\forall w\in W_*$
. For
$\forall w\in W_*$
. For
![]() $x\in K$
and
$x\in K$
and
![]() $t>0$
, we will use
$t>0$
, we will use
![]() $B_t(x)$
to denote a ball centered at x with radius t in the sense of metric R.
$B_t(x)$
to denote a ball centered at x with radius t in the sense of metric R.
We will always choose the following self-similar measure
![]() $\mu $
on K.
$\mu $
on K.
Definition 2.2 Let
![]() $\mu $
be the unique self-similar measure on K satisfying
$\mu $
be the unique self-similar measure on K satisfying
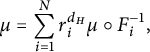 $$\begin{align*}\mu=\sum_{i=1}^N r_i^{d_H}\mu\circ F_i^{-1},\end{align*}$$
$$\begin{align*}\mu=\sum_{i=1}^N r_i^{d_H}\mu\circ F_i^{-1},\end{align*}$$
and
![]() $\mu (K)=1$
, where
$\mu (K)=1$
, where
![]() $d_H$
is determined by the equation
$d_H$
is determined by the equation
![]() $\sum _{i=1}^N r_i^{d_H}=1.$
$\sum _{i=1}^N r_i^{d_H}=1.$
In this paper, we also let
![]() $d_W=1+d_H$
and
$d_W=1+d_H$
and
![]() $d_S=\frac {2d_H}{d_W}$
.
$d_S=\frac {2d_H}{d_W}$
.
Clearly,
![]() $d_H$
is the Hausdorff dimension of K with respect to the metric R. Write
$d_H$
is the Hausdorff dimension of K with respect to the metric R. Write
![]() $\mu _i:=r_i^{d_H}$
, then we have
$\mu _i:=r_i^{d_H}$
, then we have
![]() $\mu (F_wK)=\mu _w:=\mu _{w_1}\mu _{w_2}\ldots \mu _{w_m}$
for any
$\mu (F_wK)=\mu _w:=\mu _{w_1}\mu _{w_2}\ldots \mu _{w_m}$
for any
![]() $m\geq 0,w\in W_m$
. In addition, it is well known that
$m\geq 0,w\in W_m$
. In addition, it is well known that
with some constant C independent of
![]() $x,t$
.
$x,t$
.
The exponent
![]() $d_W$
is called the walk dimension, which appears as an important index in the heat kernel estimates (see [Reference Hambly and Kumagai21]). In this paper,
$d_W$
is called the walk dimension, which appears as an important index in the heat kernel estimates (see [Reference Hambly and Kumagai21]). In this paper,
![]() $d_W=1+d_H$
holds because we use the resistance metric R. In general, this relationship is not true, for example, on the Sierpinski gasket equipped the Euclidean metric,
$d_W=1+d_H$
holds because we use the resistance metric R. In general, this relationship is not true, for example, on the Sierpinski gasket equipped the Euclidean metric,
![]() $d_W=\frac {\log 5}{\log 2}$
,
$d_W=\frac {\log 5}{\log 2}$
,
![]() $d_H=\frac {\log 3}{\log 2}$
, and so
$d_H=\frac {\log 3}{\log 2}$
, and so
![]() $d_W\neq 1+d_H$
. The exponent
$d_W\neq 1+d_H$
. The exponent
![]() $d_S$
is called the spectral dimension since it reflects the asymptotic order of the eigenvalue counting function associated with the Dirichlet form
$d_S$
is called the spectral dimension since it reflects the asymptotic order of the eigenvalue counting function associated with the Dirichlet form
![]() $(\mathcal {E},dom\mathcal {E})$
(see [Reference Kigami26, Theorem 4.2.1].
$(\mathcal {E},dom\mathcal {E})$
(see [Reference Kigami26, Theorem 4.2.1].
With the Dirichlet form
![]() $(\mathcal {E},dom\mathcal {E})$
and the self-similar measure
$(\mathcal {E},dom\mathcal {E})$
and the self-similar measure
![]() $\mu $
, we can define the associated Laplacian on K with the weak formula.
$\mu $
, we can define the associated Laplacian on K with the weak formula.
Definition 2.3 (a). Let
![]() $dom_0\mathcal {E}=\{\varphi \in dom\mathcal {E}:\varphi |_{V_0}=0\}$
. For
$dom_0\mathcal {E}=\{\varphi \in dom\mathcal {E}:\varphi |_{V_0}=0\}$
. For
![]() $f\in dom\mathcal {E}$
, say
$f\in dom\mathcal {E}$
, say
![]() $\Delta f=u$
if
$\Delta f=u$
if
(b). In addition, say
![]() $\Delta _N f=u$
if
$\Delta _N f=u$
if
Although, we will focus on Besov spaces (and Sobolev spaces) with Neumann boundary condition in this paper, it is convenient to consider
![]() $\Delta $
instead of
$\Delta $
instead of
![]() $\Delta _N$
in the proof, to enlarge the domain a little bit.
$\Delta _N$
in the proof, to enlarge the domain a little bit.
Definition 2.4 Define
![]() $\mathcal {H}_0=\{h\in dom\mathcal {E}:\Delta h=0\}$
, and call
$\mathcal {H}_0=\{h\in dom\mathcal {E}:\Delta h=0\}$
, and call
![]() $h\in \mathcal {H}_0$
a harmonic function.
$h\in \mathcal {H}_0$
a harmonic function.
In fact,
![]() $\mathcal {H}_0$
is a finite dimensional space, and each
$\mathcal {H}_0$
is a finite dimensional space, and each
![]() $h\in \mathcal {H}_0$
is uniquely determined by its boundary value on
$h\in \mathcal {H}_0$
is uniquely determined by its boundary value on
![]() $V_0$
. In particular, we can see that
$V_0$
. In particular, we can see that
![]() $\mathcal {H}_0$
is always in the
$\mathcal {H}_0$
is always in the
![]() $L^p$
domain of
$L^p$
domain of
![]() $\Delta $
for any
$\Delta $
for any
![]() $1<p<\infty $
.
$1<p<\infty $
.
2.2 Besov spaces on K
In this paper, we consider the (heat) Besov spaces
![]() $B^{p,q}_\sigma (K)$
with the Neumann boundary condition. Recall that
$B^{p,q}_\sigma (K)$
with the Neumann boundary condition. Recall that
![]() $P_t=e^{\Delta _Nt},t>0$
is a heat operator associated with
$P_t=e^{\Delta _Nt},t>0$
is a heat operator associated with
![]() $\Delta _N$
, and the Bessel potential can be defined as
$\Delta _N$
, and the Bessel potential can be defined as
![]() $(1-\Delta _N)^{-\sigma /2}=\Gamma (\sigma /2)^{-1}\int _0^\infty t^{\sigma /2-1}e^{-t}P_tdt$
. We define potential spaces on K as follows, following [Reference Hu and Zähle23] and [Reference Strichartz34].
$(1-\Delta _N)^{-\sigma /2}=\Gamma (\sigma /2)^{-1}\int _0^\infty t^{\sigma /2-1}e^{-t}P_tdt$
. We define potential spaces on K as follows, following [Reference Hu and Zähle23] and [Reference Strichartz34].
Definition 2.5 (a). For
![]() $1<p<\infty $
,
$1<p<\infty $
,
![]() $\sigma \geq 0$
, define the Sobolev space
$\sigma \geq 0$
, define the Sobolev space
with norm
![]() $\|f\|_{H^p_\sigma (K)}=\big \|(1-\Delta _N)^{\sigma /2}f\big \|_{L^p(K)}$
.
$\|f\|_{H^p_\sigma (K)}=\big \|(1-\Delta _N)^{\sigma /2}f\big \|_{L^p(K)}$
.
(b). For
![]() $1<p<\infty $
,
$1<p<\infty $
,
![]() $1\leq q\leq \infty $
and
$1\leq q\leq \infty $
and
![]() $\sigma>0$
, define the heat Besov space
$\sigma>0$
, define the heat Besov space
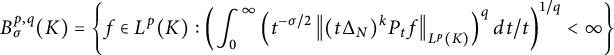 $$\begin{align*}B^{p,q}_\sigma(K)=\left\{f\in L^p(K):\left(\int_{0}^\infty \left(t^{-\sigma/2}\left\|(t\Delta_N)^kP_tf\right\|_{L^p(K)}\right)^{q}dt/t\right)^{1/q}<\infty\right\}\end{align*}$$
$$\begin{align*}B^{p,q}_\sigma(K)=\left\{f\in L^p(K):\left(\int_{0}^\infty \left(t^{-\sigma/2}\left\|(t\Delta_N)^kP_tf\right\|_{L^p(K)}\right)^{q}dt/t\right)^{1/q}<\infty\right\}\end{align*}$$
with
![]() $k\in \mathbb {N}\cap ({\sigma }/{2},\infty )$
, and norm
$k\in \mathbb {N}\cap ({\sigma }/{2},\infty )$
, and norm
![]() $\|f\|_{B^{p,q}_\sigma (K)}=\|f\|_{L^p(K)}+\left (\int _{0}^\infty (t^{-\sigma /2} \|(t\Delta _N)^k P_tf\|_{L^p(K)})^{q} dt/t\right )^{1/q}$
. We take the usual modification when
$\|f\|_{B^{p,q}_\sigma (K)}=\|f\|_{L^p(K)}+\left (\int _{0}^\infty (t^{-\sigma /2} \|(t\Delta _N)^k P_tf\|_{L^p(K)})^{q} dt/t\right )^{1/q}$
. We take the usual modification when
![]() $q=\infty $
.
$q=\infty $
.
Note that the above definition is independent of k, since different choices of k will provide equivalent norms (see [Reference Grigor'yan and Liu19] for example). The heat Besov spaces are related with Sobolev spaces by real interpolation. See book [Reference Haase20] for a proof, noticing that
![]() $\Delta _N$
is a sectorial operator. See also books [Reference Bergh and Löfström9, Reference Triebel38] for the real interpolation methods.
$\Delta _N$
is a sectorial operator. See also books [Reference Bergh and Löfström9, Reference Triebel38] for the real interpolation methods.
Lemma 2.6 Let
![]() $\sigma _1>0$
,
$\sigma _1>0$
,
![]() $1<p<\infty $
and
$1<p<\infty $
and
![]() $1\leq q\leq \infty $
. For
$1\leq q\leq \infty $
. For
![]() $0<\theta <1$
and
$0<\theta <1$
and
![]() $\sigma _\theta =\theta \sigma _1$
, we have
$\sigma _\theta =\theta \sigma _1$
, we have
In application, we will set
![]() $\sigma _1=2$
in the above lemma, where
$\sigma _1=2$
in the above lemma, where
![]() $H^p_2(K)=dom_{L^p(K)}\Delta _N:=\left \{f\in L^p(K):\Delta _Nf\in L^p(K)\right \}$
(see Sections 5 and 6 for details).
$H^p_2(K)=dom_{L^p(K)}\Delta _N:=\left \{f\in L^p(K):\Delta _Nf\in L^p(K)\right \}$
(see Sections 5 and 6 for details).
Another class of function spaces that will be studied is the Lipschitz–Besov spaces, whose definition does not rely on the Laplacian.
Definition 2.7 Let
![]() $1\leq p<\infty $
,
$1\leq p<\infty $
,
![]() $t>0$
and f be a measurable function on K, we define
$t>0$
and f be a measurable function on K, we define
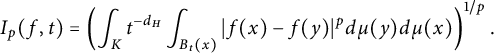 $$\begin{align*}I_p(f,t)=\left(\int_Kt^{-d_H}\int_{B_t(x)}|f(x)-f(y)|^pd\mu(y)d\mu(x)\right)^{1/p}.\end{align*}$$
$$\begin{align*}I_p(f,t)=\left(\int_Kt^{-d_H}\int_{B_t(x)}|f(x)-f(y)|^pd\mu(y)d\mu(x)\right)^{1/p}.\end{align*}$$
In addition, we define
![]() $I_\infty (f,t)=\sup \left \{|f(x)-f(y)|: x,y\in K, R(x,y)< t\right \}$
.
$I_\infty (f,t)=\sup \left \{|f(x)-f(y)|: x,y\in K, R(x,y)< t\right \}$
.
The Lipschitz–Besov spaces, denote by
![]() $\Lambda ^{p,q}_\sigma (K)$
, are defined as follows.
$\Lambda ^{p,q}_\sigma (K)$
, are defined as follows.
Definition 2.8 For
![]() $\sigma>0$
and
$\sigma>0$
and
![]() $1\leq p,q\leq \infty $
, we define
$1\leq p,q\leq \infty $
, we define
with norm
where
![]() $\|f\|_{L^q_*(0,1]}=\left (\int _0^1|f(t)|^q\frac {dt}{t}\right )^{1/q}$
and we take the usual modification when
$\|f\|_{L^q_*(0,1]}=\left (\int _0^1|f(t)|^q\frac {dt}{t}\right )^{1/q}$
and we take the usual modification when
![]() $q=\infty $
.
$q=\infty $
.
Remark 1 Since K is bounded, we can replace the integral of t over
![]() $(0,1]$
with
$(0,1]$
with
![]() $(0,\infty )$
in the above definition.
$(0,\infty )$
in the above definition.
Remark 2 Note that
![]() $I_p(f,s t)\geq \theta ^{-d_H/p}\,I_p(f,t),\forall s\in [1,\theta ]$
for each
$I_p(f,s t)\geq \theta ^{-d_H/p}\,I_p(f,t),\forall s\in [1,\theta ]$
for each
![]() $\theta>1$
and
$\theta>1$
and
![]() $1\leq p\leq \infty $
. We have
$1\leq p\leq \infty $
. We have
![]() $\big \| t^{-\sigma d_W/2} I_p(f,t)\big \|_{L^q_*(0,1]}\asymp \big \|\theta ^{m(\sigma d_W/2)} I_p(f,\theta ^{-m})\big \|_{l^q}$
, where
$\big \| t^{-\sigma d_W/2} I_p(f,t)\big \|_{L^q_*(0,1]}\asymp \big \|\theta ^{m(\sigma d_W/2)} I_p(f,\theta ^{-m})\big \|_{l^q}$
, where
![]() $\|a_m\|_{l^q}=\left (\sum _{m=0}^\infty |a_m|^q\right )^{1/q}$
if
$\|a_m\|_{l^q}=\left (\sum _{m=0}^\infty |a_m|^q\right )^{1/q}$
if
![]() $q<\infty $
and
$q<\infty $
and
![]() $\|a_m\|_{l^\infty }=\sup _{m\geq 0}|a_m|$
for each sequence of real numbers
$\|a_m\|_{l^\infty }=\sup _{m\geq 0}|a_m|$
for each sequence of real numbers
![]() $a_m,m\geq 0$
. The constants of “
$a_m,m\geq 0$
. The constants of “
![]() $\asymp $
” depend only on
$\asymp $
” depend only on
![]() $p, K$
and the harmonic structure (
$p, K$
and the harmonic structure (
![]() $H,\boldsymbol {r}$
).
$H,\boldsymbol {r}$
).
Using the above equivalent norm, we can see
3 A critical curve
In this section, we introduce a critical curve
![]() $\mathscr {C}$
in the
$\mathscr {C}$
in the
![]() $(\frac {1}{p},\sigma )$
-parameter plane as follows.
$(\frac {1}{p},\sigma )$
-parameter plane as follows.
Definition 3.1 For
![]() $1\leq p\leq \infty $
, we define
$1\leq p\leq \infty $
, we define
![]() $\mathscr {C}(p)=\sup \left \{\sigma>0:\mathcal {H}_0\subset \Lambda ^{p,\infty }_\sigma (K)\right \}$
.
$\mathscr {C}(p)=\sup \left \{\sigma>0:\mathcal {H}_0\subset \Lambda ^{p,\infty }_\sigma (K)\right \}$
.
The following proposition implies that
![]() $B^{p,q}_\sigma (K)\neq \Lambda ^{p,q}_\sigma (K)$
when
$B^{p,q}_\sigma (K)\neq \Lambda ^{p,q}_\sigma (K)$
when
![]() $\sigma>\mathscr {C}(p)$
.
$\sigma>\mathscr {C}(p)$
.
Proposition 3.2 For
![]() $1<p<\infty $
,
$1<p<\infty $
,
![]() $1\leq q\leq \infty $
,
$1\leq q\leq \infty $
,
![]() $\sigma>\mathscr C(p)$
,
$\sigma>\mathscr C(p)$
,
![]() $B^{p,q}_\sigma (K)\setminus \Lambda ^{p,q}_{\sigma }(K)\neq \emptyset $
.
$B^{p,q}_\sigma (K)\setminus \Lambda ^{p,q}_{\sigma }(K)\neq \emptyset $
.
Proof Fix
![]() $\sigma>\mathscr {C}(p)$
. First, by the definition of
$\sigma>\mathscr {C}(p)$
. First, by the definition of
![]() $\mathscr {C}(p)$
and by Remark 2 after Definition 2.8, there is
$\mathscr {C}(p)$
and by Remark 2 after Definition 2.8, there is
![]() $h\in \mathcal {H}_0$
, such that
$h\in \mathcal {H}_0$
, such that
![]() $h\notin \Lambda ^{p,q}_\sigma (K)$
. Next, we choose
$h\notin \Lambda ^{p,q}_\sigma (K)$
. Next, we choose
![]() $m\geq 1, w\in W_m$
such that
$m\geq 1, w\in W_m$
such that
![]() $F_wK\cap V_0=\emptyset $
, and fix
$F_wK\cap V_0=\emptyset $
, and fix
![]() $k\in \mathbb {N}$
so that
$k\in \mathbb {N}$
so that
![]() $2k>\sigma $
. Then one can find
$2k>\sigma $
. Then one can find
![]() $f\in H^p_{2k}(K)\subset B^{p,q}_\sigma (K)$
such that
$f\in H^p_{2k}(K)\subset B^{p,q}_\sigma (K)$
such that
![]() $f\circ F_w=h$
. The last step can be done by gluing together functions in
$f\circ F_w=h$
. The last step can be done by gluing together functions in
![]() $\{g\circ F_w:g\in dom{\mathcal E},\Delta ^k g\in C(K)\}$
with proper boundary conditions on different m-cells. We can make f smooth enough, guaranteed by Theorem 4.3 of [Reference Rogers, Strichartz and Teplyaev33]. However,
$\{g\circ F_w:g\in dom{\mathcal E},\Delta ^k g\in C(K)\}$
with proper boundary conditions on different m-cells. We can make f smooth enough, guaranteed by Theorem 4.3 of [Reference Rogers, Strichartz and Teplyaev33]. However,
![]() $f\notin \Lambda ^{p,q}_\sigma (K)$
. To show this, we note that
$f\notin \Lambda ^{p,q}_\sigma (K)$
. To show this, we note that
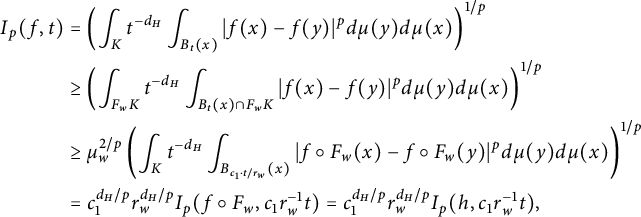 $$ \begin{align*} I_p(f,t)&=\left(\int_K t^{-d_H}\int_{B_t(x)}|f(x)-f(y)|^pd\mu(y)d\mu(x)\right)^{1/p}\\ &\geq \left(\int_{F_wK} t^{-d_H}\int_{B_t(x)\cap F_wK}|f(x)-f(y)|^pd\mu(y)d\mu(x)\right)^{1/p}\\ &\geq \mu_w^{2/p}\left(\int_K t^{-d_H}\int_{B_{c_1\cdot t/r_w}(x)}|f\circ F_w(x)-f\circ F_w(y)|^pd\mu(y)d\mu(x)\right)^{1/p}\\ &=c_1^{d_H/p}r_w^{d_H/p}I_p(f\circ F_w,{c_1}r_w^{-1}t)=c_1^{d_H/p}r_w^{d_H/p}I_p(h,c_1r_w^{-1}t), \end{align*} $$
$$ \begin{align*} I_p(f,t)&=\left(\int_K t^{-d_H}\int_{B_t(x)}|f(x)-f(y)|^pd\mu(y)d\mu(x)\right)^{1/p}\\ &\geq \left(\int_{F_wK} t^{-d_H}\int_{B_t(x)\cap F_wK}|f(x)-f(y)|^pd\mu(y)d\mu(x)\right)^{1/p}\\ &\geq \mu_w^{2/p}\left(\int_K t^{-d_H}\int_{B_{c_1\cdot t/r_w}(x)}|f\circ F_w(x)-f\circ F_w(y)|^pd\mu(y)d\mu(x)\right)^{1/p}\\ &=c_1^{d_H/p}r_w^{d_H/p}I_p(f\circ F_w,{c_1}r_w^{-1}t)=c_1^{d_H/p}r_w^{d_H/p}I_p(h,c_1r_w^{-1}t), \end{align*} $$
where we choose a finite positive constant
![]() $c_1$
such that
$c_1$
such that
![]() $F_w\left (B_{c_1t/r_w}(x)\right )\subset B_t\left (F_w(x)\right )$
for each
$F_w\left (B_{c_1t/r_w}(x)\right )\subset B_t\left (F_w(x)\right )$
for each
![]() $x\in K$
. Hence, we see that
$x\in K$
. Hence, we see that
![]() $\big \| t^{-\sigma d_W/2} I_p(f,t)\big \|_{L^q_*(0,1]}=\infty $
since
$\big \| t^{-\sigma d_W/2} I_p(f,t)\big \|_{L^q_*(0,1]}=\infty $
since
![]() $\big \| t^{-\sigma d_W/2} I_p(h,t)\big \|_{L^q_*(0,1]}=\infty $
.
$\big \| t^{-\sigma d_W/2} I_p(h,t)\big \|_{L^q_*(0,1]}=\infty $
.
3.1 Two regions
In this part, we provide some qualitative behavior of the critical curve
![]() $\mathscr C$
. We begin with the following easy observation.
$\mathscr C$
. We begin with the following easy observation.
Proposition 3.3 (a). The critical curve
![]() $\mathscr C$
is concave and increasing with respect to the parameter
$\mathscr C$
is concave and increasing with respect to the parameter
![]() $\frac {1}{p}$
. In addition,
$\frac {1}{p}$
. In addition,
![]() $\mathscr C(\infty )=\frac {2}{d_W}$
and
$\mathscr C(\infty )=\frac {2}{d_W}$
and
![]() $\mathscr C(2)=1$
.
$\mathscr C(2)=1$
.
(b). For
![]() $1\leq p\leq 2$
, we have
$1\leq p\leq 2$
, we have
![]() $1\leq \mathscr {C}(p)\leq 1+(\frac {2}{p}-1)(d_S-1)$
.
$1\leq \mathscr {C}(p)\leq 1+(\frac {2}{p}-1)(d_S-1)$
.
(c). For
![]() $2\leq p\leq \infty $
, we have
$2\leq p\leq \infty $
, we have
![]() $1+(\frac {2}{p}-1)(d_S-1)\leq \mathscr {C}(p)\leq 1\wedge (\frac {2}{d_W}+\frac {d_S}{p})$
.
$1+(\frac {2}{p}-1)(d_S-1)\leq \mathscr {C}(p)\leq 1\wedge (\frac {2}{d_W}+\frac {d_S}{p})$
.
See Figure 2 for an illustration.

Figure 2: The critical curve
![]() $\mathscr C$
in the
$\mathscr C$
in the
![]() $(\frac {1}{p},\sigma )$
-parameter plane.
$(\frac {1}{p},\sigma )$
-parameter plane.
Proof We remark that (b) and the lower bound in (c) can be derived by Proposition 5.6 in [Reference Alonso-Ruiz, Baudoin, Chen, Rogers, Shanmugalingam and Teplyaev2] and Theorem 3.11 in [Reference Alonso-Ruiz, Baudoin, Chen, Rogers, Shanmugalingam and Teplyaev4]. Since the proof is very short, we still provide an elementary proof here for completeness.
Recall Definition 2.2 that
![]() $d_W=1+d_H$
,
$d_W=1+d_H$
,
![]() $d_S=\frac {2d_H}{d_W}$
, and note that
$d_S=\frac {2d_H}{d_W}$
, and note that
![]() $d_S-1=1-\frac {2}{d_W}$
.
$d_S-1=1-\frac {2}{d_W}$
.
(a). The observation that
![]() $\mathscr {C}(\infty )=\frac {2}{d_W}$
follows from the fact that
$\mathscr {C}(\infty )=\frac {2}{d_W}$
follows from the fact that
![]() $0<\sup _{x\neq y}\frac {|h(x)-h(y)|}{R(x,y)}<\infty $
for any nonconstant harmonic function h (see [Reference Teplyaev37]). For
$0<\sup _{x\neq y}\frac {|h(x)-h(y)|}{R(x,y)}<\infty $
for any nonconstant harmonic function h (see [Reference Teplyaev37]). For
![]() $p=2$
, it is well known that
$p=2$
, it is well known that
![]() $\Lambda ^{2,\infty }_1(K)=dom\mathcal {E}$
and
$\Lambda ^{2,\infty }_1(K)=dom\mathcal {E}$
and
![]() $\Lambda ^{2,\infty }_\sigma (K)=constants$
provided
$\Lambda ^{2,\infty }_\sigma (K)=constants$
provided
![]() $\sigma>1$
(see [Reference Grigor'Yan, Hu and Lau18]), which gives
$\sigma>1$
(see [Reference Grigor'Yan, Hu and Lau18]), which gives
![]() $\mathscr {C}(2)=1$
.
$\mathscr {C}(2)=1$
.
Next, let
![]() $1\leq p_1<p_2\leq \infty $
,
$1\leq p_1<p_2\leq \infty $
,
![]() $\sigma _1<\mathscr {C}(p_1)$
and
$\sigma _1<\mathscr {C}(p_1)$
and
![]() $\sigma _2<\mathscr {C}(p_2)$
. Also, let
$\sigma _2<\mathscr {C}(p_2)$
. Also, let
![]() $s\in (0,1)$
, and let
$s\in (0,1)$
, and let
![]() $\frac {1}{p}=\frac {s}{p_1}+\frac {1-s}{p_2}$
and
$\frac {1}{p}=\frac {s}{p_1}+\frac {1-s}{p_2}$
and
![]() $\sigma =s\sigma _1+(1-s)\sigma _2$
. Then, for any
$\sigma =s\sigma _1+(1-s)\sigma _2$
. Then, for any
![]() $0<t\leq 1$
and
$0<t\leq 1$
and
![]() $h\in \mathcal {H}_0$
, it holds that
$h\in \mathcal {H}_0$
, it holds that
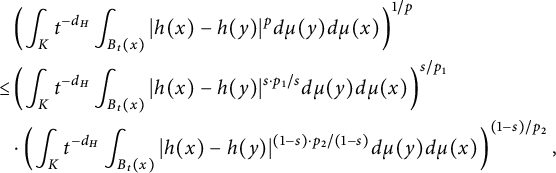 $$\begin{align*}&\left(\int_Kt^{-d_H}\int_{B_t(x)}|h(x)-h(y)|^pd\mu(y)d\mu(x)\right)^{1/p}\\\leq& \left(\int_Kt^{-d_H}\int_{B_t(x)}|h(x)-h(y)|^{s\cdot p_1/s}d\mu(y)d\mu(x)\right)^{s/p_1}\\&\cdot \left(\int_Kt^{-d_H}\int_{B_t(x)}|h(x)-h(y)|^{(1-s)\cdot p_2/(1-s)}d\mu(y)d\mu(x)\right)^{(1-s)/p_2},\end{align*}$$
$$\begin{align*}&\left(\int_Kt^{-d_H}\int_{B_t(x)}|h(x)-h(y)|^pd\mu(y)d\mu(x)\right)^{1/p}\\\leq& \left(\int_Kt^{-d_H}\int_{B_t(x)}|h(x)-h(y)|^{s\cdot p_1/s}d\mu(y)d\mu(x)\right)^{s/p_1}\\&\cdot \left(\int_Kt^{-d_H}\int_{B_t(x)}|h(x)-h(y)|^{(1-s)\cdot p_2/(1-s)}d\mu(y)d\mu(x)\right)^{(1-s)/p_2},\end{align*}$$
and thus
![]() $t^{-\sigma d_W/2}I_p(h,t)\leq t^{-\sigma d_W/2}I^s_{p_1}(h,t)I^{(1-s)}_{p_2}(h,t)\leq \|h\|^s_{\Lambda ^{p_1,\infty }_{\sigma _1}(K)}\|h\|^{1-s}_{\Lambda ^{p_2,\infty }_{\sigma _2}(K)}$
. This implies
$t^{-\sigma d_W/2}I_p(h,t)\leq t^{-\sigma d_W/2}I^s_{p_1}(h,t)I^{(1-s)}_{p_2}(h,t)\leq \|h\|^s_{\Lambda ^{p_1,\infty }_{\sigma _1}(K)}\|h\|^{1-s}_{\Lambda ^{p_2,\infty }_{\sigma _2}(K)}$
. This implies
![]() $\mathcal {H}_0\subset \Lambda ^{p,\infty }_\sigma (K)$
. Thus, we conclude
$\mathcal {H}_0\subset \Lambda ^{p,\infty }_\sigma (K)$
. Thus, we conclude
![]() $\mathscr {C}(p)\geq s\mathscr {C}(p_1)+(1-s)\mathscr {C}(p_2)$
. So
$\mathscr {C}(p)\geq s\mathscr {C}(p_1)+(1-s)\mathscr {C}(p_2)$
. So
![]() $\mathscr {C}$
is concave.
$\mathscr {C}$
is concave.
Lastly, there is a constant
![]() $C>0$
such that
$C>0$
such that
![]() $\mu (B_t(x))\leq C t^{d_H}$
for any
$\mu (B_t(x))\leq C t^{d_H}$
for any
![]() $x\in K$
and
$x\in K$
and
![]() $t\in (0,1]$
. Thus, for
$t\in (0,1]$
. Thus, for
![]() $1\leq p_1\leq p_2<\infty $
and
$1\leq p_1\leq p_2<\infty $
and
![]() $0<t\leq 1$
, it is easy to see
$0<t\leq 1$
, it is easy to see
by using the Hölder inequality. This implies that
![]() $\mathscr {C}$
is increasing with respect to
$\mathscr {C}$
is increasing with respect to
![]() $\frac 1p$
.
$\frac 1p$
.
(b). Part (b) is a consequence of part (a) and the fact that
![]() $\mathscr {C}(\infty )=\frac {2}{d_W}$
and
$\mathscr {C}(\infty )=\frac {2}{d_W}$
and
![]() $\mathscr {C}(2)=1$
.
$\mathscr {C}(2)=1$
.
(c). Now, by part (a), we can conclude that
![]() $1+(\frac {2}{p}-1)(d_S-1)\leq \mathscr {C}(p)\leq 1$
. It remains to prove
$1+(\frac {2}{p}-1)(d_S-1)\leq \mathscr {C}(p)\leq 1$
. It remains to prove
![]() $\mathscr {C}(p)\leq \frac {2}{d_W}+\frac {d_S}{p}$
. We choose a nonconstant harmonic function h such that
$\mathscr {C}(p)\leq \frac {2}{d_W}+\frac {d_S}{p}$
. We choose a nonconstant harmonic function h such that
![]() $h\circ F_1=r_1h$
, whose existence is guaranteed by Theorem A.1.2 in [Reference Kigami26]. For any
$h\circ F_1=r_1h$
, whose existence is guaranteed by Theorem A.1.2 in [Reference Kigami26]. For any
![]() $n\geq 0$
, we see that
$n\geq 0$
, we see that
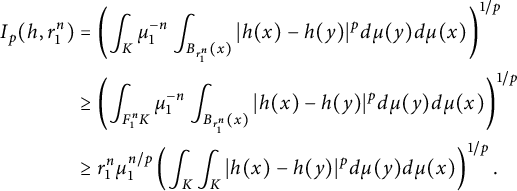 $$\begin{align*}\begin{aligned} I_p(h,r_1^n)&=\left(\int_K\mu_1^{-n}\int_{B_{r_1^n}(x)}|h(x)-h(y)|^pd\mu(y)d\mu(x)\right)^{1/p}\\ &\geq \left(\int_{F_1^nK}\mu_1^{-n}\int_{B_{r_1^n}(x)}|h(x)-h(y)|^pd\mu(y)d\mu(x)\right)^{1/p}\\ &\geq r_1^n\mu_1^{n/p}\left(\int_{K}\int_{K}|h(x)-h(y)|^pd\mu(y)d\mu(x)\right)^{1/p}. \end{aligned}\end{align*}$$
$$\begin{align*}\begin{aligned} I_p(h,r_1^n)&=\left(\int_K\mu_1^{-n}\int_{B_{r_1^n}(x)}|h(x)-h(y)|^pd\mu(y)d\mu(x)\right)^{1/p}\\ &\geq \left(\int_{F_1^nK}\mu_1^{-n}\int_{B_{r_1^n}(x)}|h(x)-h(y)|^pd\mu(y)d\mu(x)\right)^{1/p}\\ &\geq r_1^n\mu_1^{n/p}\left(\int_{K}\int_{K}|h(x)-h(y)|^pd\mu(y)d\mu(x)\right)^{1/p}. \end{aligned}\end{align*}$$
This implies that
![]() $r_1^{-\mathscr {C}(p)d_W/2}r_1^{1+d_H/p}\leq 1$
, and thus
$r_1^{-\mathscr {C}(p)d_W/2}r_1^{1+d_H/p}\leq 1$
, and thus
![]() $\mathscr {C}(p)\leq \frac {2}{d_W}+\frac {d_S}{p}$
.
$\mathscr {C}(p)\leq \frac {2}{d_W}+\frac {d_S}{p}$
.
Remark (a). When
![]() $d_W=2$
, which happens when
$d_W=2$
, which happens when
![]() $d_H=1$
for the setting of the paper, we can see that
$d_H=1$
for the setting of the paper, we can see that
![]() $\mathscr {C}(p)\equiv 1$
for
$\mathscr {C}(p)\equiv 1$
for
![]() $p\in [1,\infty ]$
by Proposition 3.3(b),(c) as
$p\in [1,\infty ]$
by Proposition 3.3(b),(c) as
![]() $d_S=1$
. This may happen when K is the unit interval, but to the best of the authors knowledge, it is unclear whether there are other interesting examples of p.c.f. self-similar sets.
$d_S=1$
. This may happen when K is the unit interval, but to the best of the authors knowledge, it is unclear whether there are other interesting examples of p.c.f. self-similar sets.
(b). When
![]() $d_W>2$
, which happens when
$d_W>2$
, which happens when
![]() $d_H>1$
for the setting of the paper, we can see
$d_H>1$
for the setting of the paper, we can see
![]() $\mathscr {C}(\infty )<1$
by Proposition 3.3(c). So according to Proposition 3.2,
$\mathscr {C}(\infty )<1$
by Proposition 3.3(c). So according to Proposition 3.2,
![]() $B^{p,q}_\sigma (K)=\Lambda ^{p,q}_\sigma (K)$
does not hold for some large p and
$B^{p,q}_\sigma (K)=\Lambda ^{p,q}_\sigma (K)$
does not hold for some large p and
![]() $\sigma <1$
.
$\sigma <1$
.
(c). For
![]() $1<p<2$
, it is possible that
$1<p<2$
, it is possible that
![]() $B^{p,q}_\sigma (K)=\Lambda ^{p,q}_\sigma (K)$
for some
$B^{p,q}_\sigma (K)=\Lambda ^{p,q}_\sigma (K)$
for some
![]() $\sigma>1$
. See the next subsection for examples with
$\sigma>1$
. See the next subsection for examples with
![]() $\mathscr {C}(1)>1$
.
$\mathscr {C}(1)>1$
.
There are two more critical lines
![]() $\mathscr {L}_1$
,
$\mathscr {L}_1$
,
![]() $\mathscr {L}_2$
in the
$\mathscr {L}_2$
in the
![]() $(\frac {1}{p},\sigma )$
-parameter plane, that are of interest, with
$(\frac {1}{p},\sigma )$
-parameter plane, that are of interest, with
where
![]() $p'=\frac {p}{p-1}$
. See Figure 3 for an illustration for the positions of
$p'=\frac {p}{p-1}$
. See Figure 3 for an illustration for the positions of
![]() $\mathscr {C},\mathscr {L}_1$
, and
$\mathscr {C},\mathscr {L}_1$
, and
![]() $\mathscr {L}_2$
. In particular, as illustrated in [Reference Grigor'Yan, Hu and Lau18, Reference Hu and Zähle23, Reference Strichartz34], the Sobolev spaces
$\mathscr {L}_2$
. In particular, as illustrated in [Reference Grigor'Yan, Hu and Lau18, Reference Hu and Zähle23, Reference Strichartz34], the Sobolev spaces
![]() $H^p_\sigma (K)$
and the heat Besov spaces
$H^p_\sigma (K)$
and the heat Besov spaces
![]() $B^{p,q}_\sigma (K)$
are embedded in
$B^{p,q}_\sigma (K)$
are embedded in
![]() $C(K)$
when the parameter point
$C(K)$
when the parameter point
![]() $(\frac {1}{p},\sigma )$
is above
$(\frac {1}{p},\sigma )$
is above
![]() $\mathscr {L}_1$
, and these function spaces with or without Neumann condition coincide if
$\mathscr {L}_1$
, and these function spaces with or without Neumann condition coincide if
![]() $(\frac {1}{p},\sigma )$
is below
$(\frac {1}{p},\sigma )$
is below
![]() $\mathscr {L}_2$
(see [Reference Cao and Qiu12–Reference Cao and Qiu14]), which clearly covers the parameter region below
$\mathscr {L}_2$
(see [Reference Cao and Qiu12–Reference Cao and Qiu14]), which clearly covers the parameter region below
![]() $\mathscr {C}$
by Proposition 3.3.
$\mathscr {C}$
by Proposition 3.3.

Figure 3: The critical curves
![]() $\mathscr L_1$
,
$\mathscr L_1$
,
![]() $\mathscr L_2$
, and
$\mathscr L_2$
, and
![]() $\mathscr C$
.
$\mathscr C$
.
In this paper, we are most interested in the region
![]() $\sigma <\mathscr {C}(p)$
, and we can see that
$\sigma <\mathscr {C}(p)$
, and we can see that
![]() $\mathscr {C}$
and
$\mathscr {C}$
and
![]() $\mathscr {L}_1$
intersect at some point with
$\mathscr {L}_1$
intersect at some point with
![]() $1\leq p\leq d_S$
by Proposition 3.3. In particular, we divide the region below
$1\leq p\leq d_S$
by Proposition 3.3. In particular, we divide the region below
![]() $\mathscr {C}$
into two parts (see Figure 4 for an illustration).
$\mathscr {C}$
into two parts (see Figure 4 for an illustration).

Figure 4: The regions
![]() $\mathscr A_1$
and
$\mathscr A_1$
and
![]() $\mathscr A_2$
.
$\mathscr A_2$
.
Region 1.
![]() $\mathscr {A}_1:=\left \{(\frac {1}{p},\sigma ): 1<p<\infty \text { and } \mathscr {L}_1(p)<\sigma <\mathscr {C}(p)\right \}$
;
$\mathscr {A}_1:=\left \{(\frac {1}{p},\sigma ): 1<p<\infty \text { and } \mathscr {L}_1(p)<\sigma <\mathscr {C}(p)\right \}$
;
Region 2.
![]() $\mathscr {A}_2:=\left \{(\frac 1 p,\sigma ): 1<p<\infty \text { and }0< \sigma <\mathscr {L}_1(p)\wedge \mathscr {C}(p)\right \}$
.
$\mathscr {A}_2:=\left \{(\frac 1 p,\sigma ): 1<p<\infty \text { and }0< \sigma <\mathscr {L}_1(p)\wedge \mathscr {C}(p)\right \}$
.
We will apply different methods when considering these two regions, for the proof of
![]() $B^{p,q}_\sigma (K)\subset \Lambda ^{p,q}_\sigma (K)$
. The border between the two regions can be dealt with by using real interpolation.
$B^{p,q}_\sigma (K)\subset \Lambda ^{p,q}_\sigma (K)$
. The border between the two regions can be dealt with by using real interpolation.
The reason that we need to divide the region
![]() $\sigma <\mathscr {C}(p)$
in this manner is due to the existence of the region
$\sigma <\mathscr {C}(p)$
in this manner is due to the existence of the region
![]() $\mathscr {C}(p)<\sigma <\mathscr {L}_1(p)$
when
$\mathscr {C}(p)<\sigma <\mathscr {L}_1(p)$
when
![]() $\mathscr {C}(1)<d_S$
. For example, this happens for the Sierpinski gasket, see the next subsection.
$\mathscr {C}(1)<d_S$
. For example, this happens for the Sierpinski gasket, see the next subsection.
3.2 Examples
In this subsection, we look at some typical p.c.f. self-similar sets, and describe their critical curves
![]() $\mathscr C$
or provide some rough estimates.
$\mathscr C$
or provide some rough estimates.
Example 1 The unit interval
![]() $I=[0,1]$
, generated by
$I=[0,1]$
, generated by
![]() $F_1(x)=\frac x 2, F_2(x)=\frac x 2+\frac 1 2$
, is a simplest example of p.c.f. self-similar sets. We equip I with the standard Laplacian, then it has walk dimension
$F_1(x)=\frac x 2, F_2(x)=\frac x 2+\frac 1 2$
, is a simplest example of p.c.f. self-similar sets. We equip I with the standard Laplacian, then it has walk dimension
![]() $d_W=2$
and spectral dimension
$d_W=2$
and spectral dimension
![]() $d_S=1$
. So the critical curve is simply a horizontal line segment,
$d_S=1$
. So the critical curve is simply a horizontal line segment,
![]() $\mathscr {C}(p)\equiv 1$
, as pointed out in the remark after Proposition 3.3.
$\mathscr {C}(p)\equiv 1$
, as pointed out in the remark after Proposition 3.3.
Example 2 A more interesting example is the Vicsek set
![]() $\mathcal {V}$
. For this example, we show that
$\mathcal {V}$
. For this example, we show that
 $$ \begin{align} \mathscr{C}(p)=1+(\frac{2}{p}-1)(d_S-1)=\frac{2\log3}{\log{15}}+\frac{2}{p}\cdot\frac{\log5-\log3}{\log15}, \end{align} $$
$$ \begin{align} \mathscr{C}(p)=1+(\frac{2}{p}-1)(d_S-1)=\frac{2\log3}{\log{15}}+\frac{2}{p}\cdot\frac{\log5-\log3}{\log15}, \end{align} $$
which corresponds to equality in two of the inequalities of Proposition 3.3(b),(c), specifically that
![]() $\mathscr {C}(p)$
is the line through (
$\mathscr {C}(p)$
is the line through (
![]() $p=\infty ,\sigma =\frac 2{d_W}$
), (
$p=\infty ,\sigma =\frac 2{d_W}$
), (
![]() $p=2,\sigma =1$
), and (
$p=2,\sigma =1$
), and (
![]() $p=1, \sigma =d_S$
). See a similar consideration in [Reference Alonso-Ruiz and Baudoin1]. In the following, we state the definition of
$p=1, \sigma =d_S$
). See a similar consideration in [Reference Alonso-Ruiz and Baudoin1]. In the following, we state the definition of
![]() $\mathcal {V}$
and show (3.1).
$\mathcal {V}$
and show (3.1).
Let
![]() $\{q_i\}_{i=1}^4$
be the four vertices of a square in
$\{q_i\}_{i=1}^4$
be the four vertices of a square in
![]() $\mathbb {R}^2$
, and let
$\mathbb {R}^2$
, and let
![]() $q_5$
be the center of the square. Define an i.f.s.
$q_5$
be the center of the square. Define an i.f.s.
![]() $\{F_i\}_{i=1}^5$
by
$\{F_i\}_{i=1}^5$
by
The Vicsek set
![]() $\mathcal {V}$
is then the unique compact set in the square such that
$\mathcal {V}$
is then the unique compact set in the square such that
![]() $\mathcal {V}=\bigcup _{i=1}^5 F_i\mathcal {V}$
(see Figure 5).
$\mathcal {V}=\bigcup _{i=1}^5 F_i\mathcal {V}$
(see Figure 5).

Figure 5: The Vicsek set
![]() $\mathcal {V}$
.
$\mathcal {V}$
.
We equip
![]() $\mathcal V$
with the fully symmetric measure
$\mathcal V$
with the fully symmetric measure
![]() $\mu $
and energy form
$\mu $
and energy form
![]() $(\mathcal E, dom\mathcal E)$
. In particular,
$(\mathcal E, dom\mathcal E)$
. In particular,
![]() $\mu $
is chosen to be the normalized Hausdorff measure on
$\mu $
is chosen to be the normalized Hausdorff measure on
![]() $\mathcal {V}$
. As for
$\mathcal {V}$
. As for
![]() $(\mathcal E, dom\mathcal E)$
, recall that it could be defined first on discrete graphs on
$(\mathcal E, dom\mathcal E)$
, recall that it could be defined first on discrete graphs on
![]() $V_m$
’s then passing to the limit. Note that
$V_m$
’s then passing to the limit. Note that
![]() $V_m=\bigcup _{w\in W_m}F_wV_{0}$
, where
$V_m=\bigcup _{w\in W_m}F_wV_{0}$
, where
![]() $V_0=\{q_1,q_2,q_3,q_4\}$
is the boundary of
$V_0=\{q_1,q_2,q_3,q_4\}$
is the boundary of
![]() $\mathcal V$
. For convenience of the later calculation, we instead to use an equivalent definition of
$\mathcal V$
. For convenience of the later calculation, we instead to use an equivalent definition of
![]() $(\mathcal E, dom\mathcal E)$
by involving the point
$(\mathcal E, dom\mathcal E)$
by involving the point
![]() $q_5$
in the graph energy forms, i.e., letting
$q_5$
in the graph energy forms, i.e., letting
![]() $\tilde {V}_0=\{q_i\}_{i=1}^5$
and
$\tilde {V}_0=\{q_i\}_{i=1}^5$
and
![]() $\tilde {V}_m=\bigcup _{w\in W_m}F_w\tilde {V}_0$
, and defining the energy form on
$\tilde {V}_m=\bigcup _{w\in W_m}F_w\tilde {V}_0$
, and defining the energy form on
![]() $\tilde {V}_0$
to be
$\tilde {V}_0$
to be
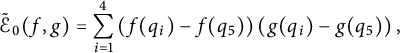 $$\begin{align*}\tilde{\mathcal{E}}_0(f,g)=\sum_{i=1}^4\left(f(q_i)-f(q_5)\right)\left(g(q_i)-g(q_5)\right),\end{align*}$$
$$\begin{align*}\tilde{\mathcal{E}}_0(f,g)=\sum_{i=1}^4\left(f(q_i)-f(q_5)\right)\left(g(q_i)-g(q_5)\right),\end{align*}$$
and iteratively
![]() $\tilde {\mathcal {E}}_m(f,g)=3\sum _{i=1}^5 \tilde {\mathcal {E}}_{m-1}(f\circ F_i, g\circ F_i)$
on
$\tilde {\mathcal {E}}_m(f,g)=3\sum _{i=1}^5 \tilde {\mathcal {E}}_{m-1}(f\circ F_i, g\circ F_i)$
on
![]() $\tilde {V}_m$
, which still approximate
$\tilde {V}_m$
, which still approximate
![]() $(\mathcal {E}, dom\mathcal {E})$
on
$(\mathcal {E}, dom\mathcal {E})$
on
![]() $\mathcal V$
. In particular, we have
$\mathcal V$
. In particular, we have
![]() $r=\frac 13$
, and in addition,
$r=\frac 13$
, and in addition,
In particular, for
![]() $h\in \mathcal {H}_0$
and
$h\in \mathcal {H}_0$
and
![]() $t\in (0,1]$
, we are interested in the estimate of
$t\in (0,1]$
, we are interested in the estimate of
![]() $I_1(h,t)$
. We denote by
$I_1(h,t)$
. We denote by
![]() $\sum _{x\sim _m y}\big |h(x)-h(y)\big |$
the sum of absolute differences of h over edges of level m, where
$\sum _{x\sim _m y}\big |h(x)-h(y)\big |$
the sum of absolute differences of h over edges of level m, where
![]() $x\sim _m y$
means that there exist a word
$x\sim _m y$
means that there exist a word
![]() $w\in W_m$
and an
$w\in W_m$
and an
![]() $1\leq i\leq 4$
such that
$1\leq i\leq 4$
such that
![]() $x=F_wq_i$
and
$x=F_wq_i$
and
![]() $y=F_wq_5$
. Since
$y=F_wq_5$
. Since
![]() $\mathcal {H}_0$
is of finite dimension, it is not hard to check that
$\mathcal {H}_0$
is of finite dimension, it is not hard to check that
On the other hand, due to the harmonic extension algorithm as shown in Figure 6, we immediately have
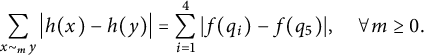 $$\begin{align*}\sum_{x\sim_m y}\big|h(x)-h(y)\big|=\sum_{i=1}^4 |f(q_i)-f(q_5)|,\quad \forall m\geq 0.\end{align*}$$
$$\begin{align*}\sum_{x\sim_m y}\big|h(x)-h(y)\big|=\sum_{i=1}^4 |f(q_i)-f(q_5)|,\quad \forall m\geq 0.\end{align*}$$
So
![]() $\sup _{m\geq 0}3^{m d_Sd_W/2}I_1(h,3^{-m})\lesssim \|h\|_\infty $
, which means
$\sup _{m\geq 0}3^{m d_Sd_W/2}I_1(h,3^{-m})\lesssim \|h\|_\infty $
, which means
![]() $h\in \Lambda ^{1,\infty }_{d_S}(\mathcal {V})$
. Thus,
$h\in \Lambda ^{1,\infty }_{d_S}(\mathcal {V})$
. Thus,
![]() $\mathscr {C}(1)=d_S$
by applying Proposition 3.3(b). This determines the formula of
$\mathscr {C}(1)=d_S$
by applying Proposition 3.3(b). This determines the formula of
![]() $\mathscr {C}(p)$
in (3.1), using Proposition 3.3(a).
$\mathscr {C}(p)$
in (3.1), using Proposition 3.3(a).

Figure 6: A harmonic function h on
![]() $\mathcal {V}$
with boundary value
$\mathcal {V}$
with boundary value
![]() $h(q_1)=a$
,
$h(q_1)=a$
,
![]() $h(q_2)=b$
,
$h(q_2)=b$
,
![]() $h(q_3)=c$
,
$h(q_3)=c$
,
![]() $h(q_4)=d$
, and
$h(q_4)=d$
, and
![]() $e=h(q_5)=(a+b+c+d)/4$
.
$e=h(q_5)=(a+b+c+d)/4$
.
The above description of
![]() $\mathscr C$
is also valid for a general
$\mathscr C$
is also valid for a general
![]() $(2k+1)$
-Vicsek set with
$(2k+1)$
-Vicsek set with
![]() $k\geq 1$
, which is generated by an i.f.s. of
$k\geq 1$
, which is generated by an i.f.s. of
![]() $4k+1$
contractions, such that each of the two cross directions of the fractal consists of
$4k+1$
contractions, such that each of the two cross directions of the fractal consists of
![]() $2k+1$
sub-cells. We omit the details. Before ending, we refer to a recent study by Baudoin and Chen [Reference Baudoin and Chen8] on the equivalent Sobolev space characterization of the domain of p-energies on
$2k+1$
sub-cells. We omit the details. Before ending, we refer to a recent study by Baudoin and Chen [Reference Baudoin and Chen8] on the equivalent Sobolev space characterization of the domain of p-energies on
![]() $\mathcal V$
.
$\mathcal V$
.
Example 3 The next example is the Sierpinski gasket
![]() ${\mathcal {SG}}$
. Let
${\mathcal {SG}}$
. Let
![]() $\{q_i\}_{i=0}^3$
be the three vertices of an equilateral triangle in
$\{q_i\}_{i=0}^3$
be the three vertices of an equilateral triangle in
![]() $\mathbb {R}^2$
, and define an i.f.s.
$\mathbb {R}^2$
, and define an i.f.s.
![]() $\{F_i\}_{i=1}^3$
by
$\{F_i\}_{i=1}^3$
by
The Sierpinski gasket
![]() $\mathcal {SG}$
is the unique compact set in
$\mathcal {SG}$
is the unique compact set in
![]() $\mathbb {R}^2$
such that
$\mathbb {R}^2$
such that
![]() ${\mathcal {SG}}=\bigcup _{i=1}^3 F_i{\mathcal {SG}}$
(see Figure 7).
${\mathcal {SG}}=\bigcup _{i=1}^3 F_i{\mathcal {SG}}$
(see Figure 7).

Figure 7: The Sierpinski gasket
![]() ${\mathcal {SG}}$
.
${\mathcal {SG}}$
.
On
![]() ${\mathcal {SG}}$
, we take the normalized Hausdorff measure
${\mathcal {SG}}$
, we take the normalized Hausdorff measure
![]() $\mu $
and the standard energy form
$\mu $
and the standard energy form
![]() $(\mathcal {E}, dom\mathcal E)$
satisfying
$(\mathcal {E}, dom\mathcal E)$
satisfying
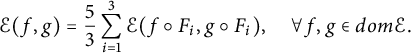 $$\begin{align*}\mathcal{E}(f,g)=\frac{5}{3}\sum_{i=1}^3\mathcal{E}(f\circ F_i, g\circ F_i), \quad \forall f,g\in dom\mathcal{E}.\end{align*}$$
$$\begin{align*}\mathcal{E}(f,g)=\frac{5}{3}\sum_{i=1}^3\mathcal{E}(f\circ F_i, g\circ F_i), \quad \forall f,g\in dom\mathcal{E}.\end{align*}$$
In particular, we have
![]() $r=\frac 3 5$
, and in addition,
$r=\frac 3 5$
, and in addition,
It seems hard to get the exact formula of
![]() $\mathscr {C}(p)$
. However, by a simple calculation, we can see that
$\mathscr {C}(p)$
. However, by a simple calculation, we can see that
![]() $\mathscr {C}(p)$
is indeed a “curve” by observing that
$\mathscr {C}(p)$
is indeed a “curve” by observing that
![]() $1<\mathscr C(1)<d_S$
, and then using Proposition 3.3. In fact, this can be verified by estimating the maximal exponential growth ratio of
$1<\mathscr C(1)<d_S$
, and then using Proposition 3.3. In fact, this can be verified by estimating the maximal exponential growth ratio of
![]() $\sum _{x\sim _m y}\big |h(x)-h(y)\big |$
as
$\sum _{x\sim _m y}\big |h(x)-h(y)\big |$
as
![]() $m\rightarrow \infty $
, which should be
$m\rightarrow \infty $
, which should be
![]() $ r^{\mathscr C(1)d_W/2-d_H}$
for harmonic functions h on
$ r^{\mathscr C(1)d_W/2-d_H}$
for harmonic functions h on
![]() $\mathcal {SG}$
. Since any harmonic function h is a combination of
$\mathcal {SG}$
. Since any harmonic function h is a combination of
![]() $h_1, h_2, h_3$
with
$h_1, h_2, h_3$
with
![]() $h_i(q_j)=\delta _{i,j}$
, by calculating
$h_i(q_j)=\delta _{i,j}$
, by calculating
![]() $\sum _{x\sim _m y}\big |h_1(x)-h_1(y)\big |$
with
$\sum _{x\sim _m y}\big |h_1(x)-h_1(y)\big |$
with
![]() $m=3$
, we see that
$m=3$
, we see that
Lastly, we remark that the fact
![]() $1<\mathscr C(1)<d_S$
is also indicated by Theorem 5.2 of [Reference Alonso-Ruiz, Baudoin, Chen, Rogers, Shanmugalingam and Teplyaev4].
$1<\mathscr C(1)<d_S$
is also indicated by Theorem 5.2 of [Reference Alonso-Ruiz, Baudoin, Chen, Rogers, Shanmugalingam and Teplyaev4].
4 Discrete characterizations of
 $\Lambda ^{p,q}_\sigma (K)$
$\Lambda ^{p,q}_\sigma (K)$
In this section, we will provide some discrete characterizations of the Lipschitz–Besov spaces
![]() $\Lambda ^{p,q}_\sigma (K)$
. These characterizations will provide great convenience in proving Theorem 1.1. In particular, they heavily rely on the nested structure of K.
$\Lambda ^{p,q}_\sigma (K)$
. These characterizations will provide great convenience in proving Theorem 1.1. In particular, they heavily rely on the nested structure of K.
Definition 4.1 (a). For
![]() $m\geq 0$
, define
$m\geq 0$
, define
![]() $\Lambda _m=\{w\in W_*:r_w\leq r^m<r_{w^*}\}$
with
$\Lambda _m=\{w\in W_*:r_w\leq r^m<r_{w^*}\}$
with
![]() $r=\min _{1\leq i\leq N}r_i$
. In particular, we denote
$r=\min _{1\leq i\leq N}r_i$
. In particular, we denote
![]() $\Lambda _0={\{\emptyset \}}$
.
$\Lambda _0={\{\emptyset \}}$
.
(b). Define
![]() $V_{\Lambda _m}=\bigcup _{w\in \Lambda _m} F_wV_0$
for
$V_{\Lambda _m}=\bigcup _{w\in \Lambda _m} F_wV_0$
for
![]() $m\geq 0$
, and denote
$m\geq 0$
, and denote
 $$ \begin{align*}\mathring{V}_{\Lambda_m}= \begin{cases} V_0,&\text{ if }m=0,\\ V_{\Lambda_m}\setminus V_{\Lambda_{m-1}},&\text{ if }m\geq 1. \end{cases}\end{align*} $$
$$ \begin{align*}\mathring{V}_{\Lambda_m}= \begin{cases} V_0,&\text{ if }m=0,\\ V_{\Lambda_m}\setminus V_{\Lambda_{m-1}},&\text{ if }m\geq 1. \end{cases}\end{align*} $$
In the rest of this section, we will consider two kinds of discrete characterizations of
![]() $\Lambda ^{p,q}_\sigma (K)$
, basing on the cell graphs approximation and vertex graphs approximation of K, respectively.
$\Lambda ^{p,q}_\sigma (K)$
, basing on the cell graphs approximation and vertex graphs approximation of K, respectively.
4.1 A Haar series expansion
We begin with a Haar series expansion of a function. We classify Haar functions on K into different levels based on the partition
![]() $\Lambda _m$
.
$\Lambda _m$
.
Definition 4.2 (a). For each
![]() $f\in L^1(K)$
, we define
$f\in L^1(K)$
, we define
![]() $E_w(f)=\frac {1}{\mu _w}\int _{F_wK}fd\mu $
, and write
$E_w(f)=\frac {1}{\mu _w}\int _{F_wK}fd\mu $
, and write
which can be understood as the conditional expectation of f with respect to the sigma algebra generated by the collection
![]() $\{F_wK: w\in \Lambda _m\}$
. In addition, we write
$\{F_wK: w\in \Lambda _m\}$
. In addition, we write
 $$\begin{align*}\tilde{E}[f|\Lambda_m]=\begin{cases} E[f|\Lambda_0], &\text{ if }m=0,\\ E[f|\Lambda_m]-E[f|\Lambda_{m-1}], &\text{ if }m\geq 1. \end{cases}\end{align*}$$
$$\begin{align*}\tilde{E}[f|\Lambda_m]=\begin{cases} E[f|\Lambda_0], &\text{ if }m=0,\\ E[f|\Lambda_m]-E[f|\Lambda_{m-1}], &\text{ if }m\geq 1. \end{cases}\end{align*}$$
(b). Define
![]() $\tilde {J}_m=\left \{\tilde {E}[f|\Lambda _m]:f\in L^1(K)\right \}$
, and call
$\tilde {J}_m=\left \{\tilde {E}[f|\Lambda _m]:f\in L^1(K)\right \}$
, and call
![]() $\tilde {J}_m$
the space of level-m Haar functions.
$\tilde {J}_m$
the space of level-m Haar functions.
It is easy to see that, for
![]() $m\geq 1$
,
$m\geq 1$
,
![]() $\tilde {J}_m$
consists of functions u which are piecewise constant on
$\tilde {J}_m$
consists of functions u which are piecewise constant on
![]() $\{F_wK: w\in \Lambda _m\}$
, and satisfy
$\{F_wK: w\in \Lambda _m\}$
, and satisfy
![]() $E[u|\Lambda _{m-1}]=0$
. We have the following estimates.
$E[u|\Lambda _{m-1}]=0$
. We have the following estimates.
Lemma 4.3 Let
![]() $f\in L^p(K)$
with
$f\in L^p(K)$
with
![]() $1<p<\infty $
and
$1<p<\infty $
and
![]() $u\in \tilde {J}_m$
with
$u\in \tilde {J}_m$
with
![]() $m\geq 0$
. Then:
$m\geq 0$
. Then:
(a).
![]() $\big \|\tilde {E}[f|\Lambda _m]\big \|_{L^p(K)}\leq C I_p(f,r^{m-1})$
for any
$\big \|\tilde {E}[f|\Lambda _m]\big \|_{L^p(K)}\leq C I_p(f,r^{m-1})$
for any
![]() $m\geq 1$
.
$m\geq 1$
.
(b).
![]() $I_p(f,t)\leq C\|f\|_{L^p(K)}$
for any
$I_p(f,t)\leq C\|f\|_{L^p(K)}$
for any
![]() $0<t\leq 1$
.
$0<t\leq 1$
.
(c).
![]() $I_p(u,r^n)\leq Cr^{(n-m)d_H/p}\|u\|_{L^p(K)}$
for any
$I_p(u,r^n)\leq Cr^{(n-m)d_H/p}\|u\|_{L^p(K)}$
for any
![]() $n\geq m$
.
$n\geq m$
.
The constant C can be chosen to be independent of
![]() $f,u$
, and p.
$f,u$
, and p.
Proof (a). For each point
![]() $x\in K\setminus V_{\Lambda _m}$
, we define
$x\in K\setminus V_{\Lambda _m}$
, we define
![]() $Z_{\Lambda _m}(x)=F_wK$
with
$Z_{\Lambda _m}(x)=F_wK$
with
![]() $w\in \Lambda _{m}$
such that
$w\in \Lambda _{m}$
such that
![]() $x\in F_wK$
. Clearly, we have
$x\in F_wK$
. Clearly, we have
![]() $Z_{\Lambda _m}(x)\subset B_{r^{m}}(x)$
since the diameter of each cell
$Z_{\Lambda _m}(x)\subset B_{r^{m}}(x)$
since the diameter of each cell
![]() $F_wK,w\in \Lambda _m$
is at most
$F_wK,w\in \Lambda _m$
is at most
![]() $r^{m}$
. For
$r^{m}$
. For
![]() $m\geq 1$
, we have
$m\geq 1$
, we have
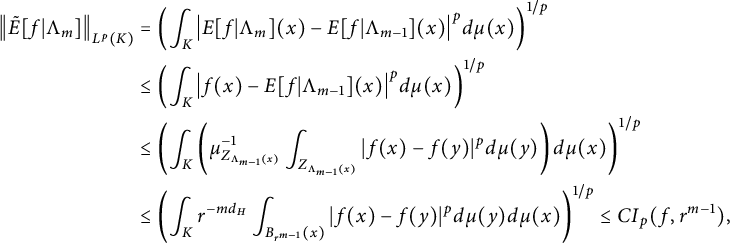 $$\begin{align*}\begin{aligned} \left\|\tilde{E}[f|\Lambda_m]\right\|_{L^p(K)}&=\left(\int_{K}\big|E[f|\Lambda_m](x)-E[f|\Lambda_{m-1}](x)\big|^pd\mu(x)\right)^{1/p}\\ &\leq \left(\int_{K}\big|f(x)-{E}[f|\Lambda_{m-1}](x)\big|^pd\mu(x)\right)^{1/p}\\ &\leq \left(\int_K\left(\mu_{Z_{{\Lambda_{m-1}(x)}}}^{-1}\int_{Z_{\Lambda_{m-1}(x)}}|f(x)-f(y)|^pd\mu(y)\right)d\mu(x)\right)^{1/p}\\ &\leq \left(\int_Kr^{-md_H}\int_{B_{r^{m-1}}(x)}|f(x)-f(y)|^pd\mu(y)d\mu(x)\right)^{1/p}\leq CI_p(f,r^{m-1}), \end{aligned}\end{align*}$$
$$\begin{align*}\begin{aligned} \left\|\tilde{E}[f|\Lambda_m]\right\|_{L^p(K)}&=\left(\int_{K}\big|E[f|\Lambda_m](x)-E[f|\Lambda_{m-1}](x)\big|^pd\mu(x)\right)^{1/p}\\ &\leq \left(\int_{K}\big|f(x)-{E}[f|\Lambda_{m-1}](x)\big|^pd\mu(x)\right)^{1/p}\\ &\leq \left(\int_K\left(\mu_{Z_{{\Lambda_{m-1}(x)}}}^{-1}\int_{Z_{\Lambda_{m-1}(x)}}|f(x)-f(y)|^pd\mu(y)\right)d\mu(x)\right)^{1/p}\\ &\leq \left(\int_Kr^{-md_H}\int_{B_{r^{m-1}}(x)}|f(x)-f(y)|^pd\mu(y)d\mu(x)\right)^{1/p}\leq CI_p(f,r^{m-1}), \end{aligned}\end{align*}$$
where we ignore the finitely many points in
![]() $V_{\Lambda _m}$
in the above estimate.
$V_{\Lambda _m}$
in the above estimate.
(b) is obvious, and C only depends on the estimate
![]() $\mu (B_t(x))\lesssim t^{d_H}$
.
$\mu (B_t(x))\lesssim t^{d_H}$
.
(c). First, we have the estimate that
 $$ \begin{align} \begin{aligned} \|u\|_{L^p(K)}&=\left(\sum_{w\in\Lambda_m}\mu_w|E_w(u)|^p\right)^{1/p}\geq \left(r^{(m+1)d_H}\sum_{w\in \Lambda_m}|E_w(u)|^p\right)^{1/p}\\ &\gtrsim r^{md_H/p}\left(\sum_{w\sim w'\text{ in }\Lambda_m}|E_w(u)-E_{w'}(u)|^p\right)^{1/p}, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \|u\|_{L^p(K)}&=\left(\sum_{w\in\Lambda_m}\mu_w|E_w(u)|^p\right)^{1/p}\geq \left(r^{(m+1)d_H}\sum_{w\in \Lambda_m}|E_w(u)|^p\right)^{1/p}\\ &\gtrsim r^{md_H/p}\left(\sum_{w\sim w'\text{ in }\Lambda_m}|E_w(u)-E_{w'}(u)|^p\right)^{1/p}, \end{aligned} \end{align} $$
where we write
![]() $w\sim w'$
if
$w\sim w'$
if
![]() $w\neq w'$
and
$w\neq w'$
and
![]() $F_wK\cap F_{w'}K\neq \emptyset $
, and use the fact that
$F_wK\cap F_{w'}K\neq \emptyset $
, and use the fact that
![]() $\#\{w'\in \Lambda _m:w'\sim w\}\leq \#V_0\#\mathcal {C}$
for any
$\#\{w'\in \Lambda _m:w'\sim w\}\leq \#V_0\#\mathcal {C}$
for any
![]() $w\in \Lambda _m$
.
$w\in \Lambda _m$
.
Next, notice that there is
![]() $k>0$
such that
$k>0$
such that
![]() $R(x,y)>r^n$
for any
$R(x,y)>r^n$
for any
![]() $m\geq 0$
,
$m\geq 0$
,
![]() $n\geq m+k$
and
$n\geq m+k$
and
![]() $x\in F_wK, y\in F_{w'}K$
with
$x\in F_wK, y\in F_{w'}K$
with
![]() $F_wK\cap F_{w'}K=\emptyset $
,
$F_wK\cap F_{w'}K=\emptyset $
,
![]() $w,w'\in \Lambda _m$
. It suffices to consider
$w,w'\in \Lambda _m$
. It suffices to consider
![]() $n\geq m+k$
, since for
$n\geq m+k$
, since for
![]() $n<m+k$
we have (b). For
$n<m+k$
we have (b). For
![]() $n\geq m+k$
, we have the estimate
$n\geq m+k$
, we have the estimate
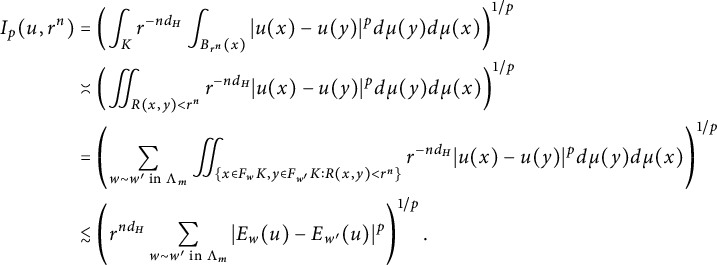 $$\begin{align*}\begin{aligned} I_p(u,r^n)&=\left(\int_Kr^{-nd_H}\int_{B_{r^{n}}(x)}|u(x)-u(y)|^pd\mu(y)d\mu(x)\right)^{1/p}\\ &\asymp \left(\iint_{R(x,y)<r^n}r^{-nd_H}|u(x)-u(y)|^pd\mu(y)d\mu(x)\right)^{1/p}\\ &=\left(\sum_{w\sim w'\text{ in }\Lambda_m}\iint_{\{x\in F_wK,y\in F_{w'}K:R(x,y)<r^n \}}r^{-nd_H}|u(x)-u(y)|^pd\mu(y)d\mu(x)\right)^{1/p}\\ &\lesssim \left(r^{nd_H}\sum_{w\sim w'\text{ in }\Lambda_m}|E_w(u)-E_{w'}(u)|^p\right)^{1/p}. \end{aligned}\end{align*}$$
$$\begin{align*}\begin{aligned} I_p(u,r^n)&=\left(\int_Kr^{-nd_H}\int_{B_{r^{n}}(x)}|u(x)-u(y)|^pd\mu(y)d\mu(x)\right)^{1/p}\\ &\asymp \left(\iint_{R(x,y)<r^n}r^{-nd_H}|u(x)-u(y)|^pd\mu(y)d\mu(x)\right)^{1/p}\\ &=\left(\sum_{w\sim w'\text{ in }\Lambda_m}\iint_{\{x\in F_wK,y\in F_{w'}K:R(x,y)<r^n \}}r^{-nd_H}|u(x)-u(y)|^pd\mu(y)d\mu(x)\right)^{1/p}\\ &\lesssim \left(r^{nd_H}\sum_{w\sim w'\text{ in }\Lambda_m}|E_w(u)-E_{w'}(u)|^p\right)^{1/p}. \end{aligned}\end{align*}$$
Combining this with the estimate (4.1), we get (c).
Using Lemma 4.3, we can prove a Haar function decomposition of the spaces
![]() $\Lambda ^{p,q}_\sigma (K)$
for
$\Lambda ^{p,q}_\sigma (K)$
for
![]() $0<\sigma <\mathscr {L}_1(p)$
.
$0<\sigma <\mathscr {L}_1(p)$
.
Proposition 4.4 For
![]() $1<p<\infty $
,
$1<p<\infty $
,
![]() $1\leq q\leq \infty $
and
$1\leq q\leq \infty $
and
![]() $0<\sigma <\mathscr {L}_1(p)=\frac {d_S}{p}$
, we have
$0<\sigma <\mathscr {L}_1(p)=\frac {d_S}{p}$
, we have
![]() $f\in \Lambda ^{p,q}_\sigma (K)$
if and only if
$f\in \Lambda ^{p,q}_\sigma (K)$
if and only if
![]() $\big \|r^{-m\sigma d_W/2}\|\tilde {E}[f|\Lambda _m]\|_{L^p(K)}\big \|_{l^q}<\infty $
. In addition,
$\big \|r^{-m\sigma d_W/2}\|\tilde {E}[f|\Lambda _m]\|_{L^p(K)}\big \|_{l^q}<\infty $
. In addition,
![]() $\|f\|_{\Lambda ^{p,q}_\sigma (K)}\asymp \big \|r^{-m\sigma d_W/2}\|\tilde {E}[f|{\Lambda _m}]\|_{L^p(K)}\big \|_{l^q}$
.
$\|f\|_{\Lambda ^{p,q}_\sigma (K)}\asymp \big \|r^{-m\sigma d_W/2}\|\tilde {E}[f|{\Lambda _m}]\|_{L^p(K)}\big \|_{l^q}$
.
Proof We first observe that
By using Lemma 4.3(a), we then easily see that
For the other direction, we write
![]() $f_m=\tilde {E}[f|\Lambda _m]$
for
$f_m=\tilde {E}[f|\Lambda _m]$
for
![]() $m\geq 0$
, and assume that
$m\geq 0$
, and assume that
First of all, by the Martingale convergence theorem, we see that
![]() $E[f|\Lambda _{m'}]=\sum _{m=0}^{m'}f_m\to f$
strongly in
$E[f|\Lambda _{m'}]=\sum _{m=0}^{m'}f_m\to f$
strongly in
![]() $L^p(K)$
as
$L^p(K)$
as
![]() $m'\to \infty $
, so
$m'\to \infty $
, so
 $$ \begin{align} \begin{aligned} \|f\|_{L^p(K)}=\lim\limits_{m'\to\infty}\left\|E[f|\Lambda_{m'}]\right\|_{L^p(K)}&\leq \sum_{m=0}^\infty\left\|f_m\right\|_{L^p(K)}\\&\leq \left\|r^{m\sigma d_W/2}\right\|_{l^{q'}}\cdot\left\|r^{-m\sigma d_W/2}\|f_m\|_{L^p(K)}\right\|_{l^q} \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \|f\|_{L^p(K)}=\lim\limits_{m'\to\infty}\left\|E[f|\Lambda_{m'}]\right\|_{L^p(K)}&\leq \sum_{m=0}^\infty\left\|f_m\right\|_{L^p(K)}\\&\leq \left\|r^{m\sigma d_W/2}\right\|_{l^{q'}}\cdot\left\|r^{-m\sigma d_W/2}\|f_m\|_{L^p(K)}\right\|_{l^q} \end{aligned} \end{align} $$
with
![]() $q'=\frac {q}{q-1}$
. Next, we notice that
$q'=\frac {q}{q-1}$
. Next, we notice that
 $$ \begin{align} \left\|r^{-m\sigma d_W/2}I_p(f,r^m)\right\|_{l^q}\leq \left\|\sum_{n=0}^{m-1} r^{-m\sigma d_W/2}I_p(f_n,r^m)\right\|_{l^q}+\left\|\sum_{n=m}^{\infty} r^{-m\sigma d_W/2}I_p(f_n,r^m)\right\|_{l^q} \end{align} $$
$$ \begin{align} \left\|r^{-m\sigma d_W/2}I_p(f,r^m)\right\|_{l^q}\leq \left\|\sum_{n=0}^{m-1} r^{-m\sigma d_W/2}I_p(f_n,r^m)\right\|_{l^q}+\left\|\sum_{n=m}^{\infty} r^{-m\sigma d_W/2}I_p(f_n,r^m)\right\|_{l^q} \end{align} $$
with
 $$ \begin{align} \begin{aligned} \left\|\sum_{n=0}^{m-1} r^{-m\sigma d_W/2}I_p(f_n,r^m)\right\|_{l^q}&\lesssim \left\|\sum_{n=0}^{m-1} r^{-m\sigma d_W/2+(m-n)d_H/p}\|f_n\|_{L^p(K)}\right\|_{l^q}\\ &=\left\|\sum_{n=1}^{m} r^{-m\sigma d_W/2+nd_H/p}\|f_{m-n}\|_{L^p(K)}\right\|_{l^q}\\ &=\left\|\sum_{n=1}^{m} r^{-(m-n)\sigma d_W/2+n(d_H/p-\sigma d_W/2)}\|f_{m-n}\|_{L^p(K)}\right\|_{l^q}\\ &\leq\left(\sum_{n=1}^\infty r^{n(d_H/p-\sigma d_W/2)}\right)\cdot\left\|r^{-m\sigma d_W/2}\|f_m\|_{L^p(K)}\right\|_{l^q} \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \left\|\sum_{n=0}^{m-1} r^{-m\sigma d_W/2}I_p(f_n,r^m)\right\|_{l^q}&\lesssim \left\|\sum_{n=0}^{m-1} r^{-m\sigma d_W/2+(m-n)d_H/p}\|f_n\|_{L^p(K)}\right\|_{l^q}\\ &=\left\|\sum_{n=1}^{m} r^{-m\sigma d_W/2+nd_H/p}\|f_{m-n}\|_{L^p(K)}\right\|_{l^q}\\ &=\left\|\sum_{n=1}^{m} r^{-(m-n)\sigma d_W/2+n(d_H/p-\sigma d_W/2)}\|f_{m-n}\|_{L^p(K)}\right\|_{l^q}\\ &\leq\left(\sum_{n=1}^\infty r^{n(d_H/p-\sigma d_W/2)}\right)\cdot\left\|r^{-m\sigma d_W/2}\|f_m\|_{L^p(K)}\right\|_{l^q} \end{aligned} \end{align} $$
by using Lemma 4.3(c) and the Minkowski inequality, and
 $$ \begin{align} \begin{aligned} \left\|\sum_{n=m}^{\infty} r^{-m\sigma d_W/2}I_p(f_n,r^m)\right\|_{l^q}&\lesssim \left\|\sum_{n=m}^{\infty} r^{-m\sigma d_W/2}\|f_n\|_{L^p(K)}\right\|_{l^q}\\ &=\left\|\sum_{n=0}^{\infty} r^{-m\sigma d_W/2}\|f_{n+m}\|_{L^p(K)}\right\|_{l^q}\\ &\leq \left(\sum_{n=0}^\infty r^{n\sigma d_W/2}\right)\cdot\left\| r^{-m\sigma d_W/2}\|f_m\|_{L^p(K)}\right\|_{l^q} \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \left\|\sum_{n=m}^{\infty} r^{-m\sigma d_W/2}I_p(f_n,r^m)\right\|_{l^q}&\lesssim \left\|\sum_{n=m}^{\infty} r^{-m\sigma d_W/2}\|f_n\|_{L^p(K)}\right\|_{l^q}\\ &=\left\|\sum_{n=0}^{\infty} r^{-m\sigma d_W/2}\|f_{n+m}\|_{L^p(K)}\right\|_{l^q}\\ &\leq \left(\sum_{n=0}^\infty r^{n\sigma d_W/2}\right)\cdot\left\| r^{-m\sigma d_W/2}\|f_m\|_{L^p(K)}\right\|_{l^q} \end{aligned} \end{align} $$
by using Lemma 4.3(b) and the Minkowski inequality again.
Combining equations 4.2–4.6, and noticing that
![]() $0<\sigma <\frac {d_S}{p}$
, we get
$0<\sigma <\frac {d_S}{p}$
, we get
The proposition follows.
4.2 Graph Laplacians and a tent function decomposition
Now, we turn to the case when
![]() $\sigma>\mathscr {L}_1(p)$
. In this case, we have
$\sigma>\mathscr {L}_1(p)$
. In this case, we have
![]() $B^{p,q}_\sigma (K)\subset C(K)$
as a well-known result[Reference Hu and Zähle23], and we would expect this to happen for
$B^{p,q}_\sigma (K)\subset C(K)$
as a well-known result[Reference Hu and Zähle23], and we would expect this to happen for
![]() $\Lambda ^{p,q}_\sigma (K)$
. This can be easily seen from the following lemma.
$\Lambda ^{p,q}_\sigma (K)$
. This can be easily seen from the following lemma.
Lemma 4.5 Let
![]() $1<p<\infty $
and
$1<p<\infty $
and
![]() $f\in L^p(K)$
, we define
$f\in L^p(K)$
, we define
![]() $E_{B_t(x)}(f)=\frac 1{\mu (B_t(x))}\int _{B_t(x)}fd\mu $
for any
$E_{B_t(x)}(f)=\frac 1{\mu (B_t(x))}\int _{B_t(x)}fd\mu $
for any
![]() $x\in K$
and
$x\in K$
and
![]() $0<t\leq 1$
. Then we have:
$0<t\leq 1$
. Then we have:
(a). If
![]() $\{x_j\}_{j=1}^n\subset K$
is a finite set of points such that
$\{x_j\}_{j=1}^n\subset K$
is a finite set of points such that
![]() $\sum _{j=1}^n 1_{B_{rt}(x_j)}\leq \lambda $
for some finite number
$\sum _{j=1}^n 1_{B_{rt}(x_j)}\leq \lambda $
for some finite number
![]() $\lambda <\infty $
, then
$\lambda <\infty $
, then
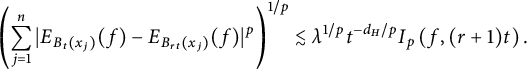 $$\begin{align*}\left(\sum_{j=1}^n |E_{B_t(x_j)}(f)-E_{B_{rt}(x_j)}(f)|^p\right)^{1/p}\lesssim \lambda^{1/p} t^{-d_H/p}I_p\left(f,(r+1)t\right).\end{align*}$$
$$\begin{align*}\left(\sum_{j=1}^n |E_{B_t(x_j)}(f)-E_{B_{rt}(x_j)}(f)|^p\right)^{1/p}\lesssim \lambda^{1/p} t^{-d_H/p}I_p\left(f,(r+1)t\right).\end{align*}$$
(b). For
![]() $1\leq q\leq \infty $
,
$1\leq q\leq \infty $
,
![]() $\Lambda ^{p,q}_\sigma (K)\subset C^{\sigma d_W/2-d_H/p}(K)$
for
$\Lambda ^{p,q}_\sigma (K)\subset C^{\sigma d_W/2-d_H/p}(K)$
for
![]() $\sigma>\frac {d_S}{p}$
, where
$\sigma>\frac {d_S}{p}$
, where
![]() $C^{\sigma d_W/2-d_H/p}(K)$
denotes the space of Hölder continuous functions on
$C^{\sigma d_W/2-d_H/p}(K)$
denotes the space of Hölder continuous functions on
![]() $(K,R)$
with exponent
$(K,R)$
with exponent
![]() $\sigma d_W/2-d_H/p$
.
$\sigma d_W/2-d_H/p$
.
Proof (a) follows from a direct estimate,
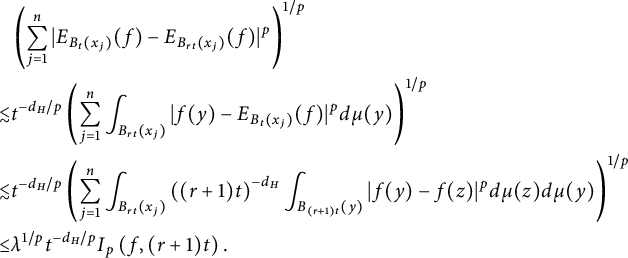 $$\begin{align*}\begin{aligned} &\left(\sum_{j=1}^n |E_{B_t(x_j)}(f)-E_{B_{rt}(x_j)}(f)|^p\right)^{1/p}\\ \lesssim& t^{-d_H/p}\left(\sum_{j=1}^n\int_{B_{rt}(x_j)}|f(y)-E_{B_t(x_j)}(f)|^pd\mu(y)\right)^{1/p}\\ \lesssim& t^{-d_H/p}\left(\sum_{j=1}^n\int_{B_{rt}(x_j)}\left((r+1)t\right)^{-d_H}\int_{B_{(r+1)t}(y)}|f(y)-f(z)|^pd\mu(z)d\mu(y)\right)^{1/p}\\ \leq &\lambda^{1/p}t^{-d_H/p}I_p\left(f,(r+1)t\right). \end{aligned}\end{align*}$$
$$\begin{align*}\begin{aligned} &\left(\sum_{j=1}^n |E_{B_t(x_j)}(f)-E_{B_{rt}(x_j)}(f)|^p\right)^{1/p}\\ \lesssim& t^{-d_H/p}\left(\sum_{j=1}^n\int_{B_{rt}(x_j)}|f(y)-E_{B_t(x_j)}(f)|^pd\mu(y)\right)^{1/p}\\ \lesssim& t^{-d_H/p}\left(\sum_{j=1}^n\int_{B_{rt}(x_j)}\left((r+1)t\right)^{-d_H}\int_{B_{(r+1)t}(y)}|f(y)-f(z)|^pd\mu(z)d\mu(y)\right)^{1/p}\\ \leq &\lambda^{1/p}t^{-d_H/p}I_p\left(f,(r+1)t\right). \end{aligned}\end{align*}$$
(b). Let
![]() $f\in \Lambda ^{p,q}_\sigma (K)$
. By the Lebesgue differentiation theorem, we know that
$f\in \Lambda ^{p,q}_\sigma (K)$
. By the Lebesgue differentiation theorem, we know that
![]() $f(x)=\lim _{m\to \infty } E_{B_{r^m}(x)}(f)$
for
$f(x)=\lim _{m\to \infty } E_{B_{r^m}(x)}(f)$
for
![]() $\mu $
-a.e.
$\mu $
-a.e.
![]() $x\in K$
. For such x and
$x\in K$
. For such x and
![]() $m\geq 0$
,
$m\geq 0$
,
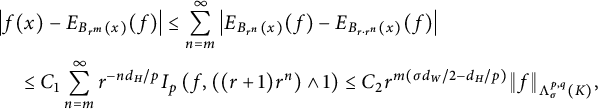 $$\begin{align*}\begin{aligned} &\big|f(x)-E_{B_{r^m}(x)}(f)\big|\leq \sum_{n=m}^\infty\big|E_{B_{r^n}(x)}(f)-E_{B_{r\cdot r^n}(x)}(f)\big|\\ & \quad\leq C_1\sum_{n=m}^\infty r^{-nd_H/p}I_p\left(f,\left((r+1)r^n\right)\wedge 1\right)\leq C_2r^{m(\sigma d_W/2-d_H/p)}\|f\|_{\Lambda^{p,q}_\sigma(K)}, \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} &\big|f(x)-E_{B_{r^m}(x)}(f)\big|\leq \sum_{n=m}^\infty\big|E_{B_{r^n}(x)}(f)-E_{B_{r\cdot r^n}(x)}(f)\big|\\ & \quad\leq C_1\sum_{n=m}^\infty r^{-nd_H/p}I_p\left(f,\left((r+1)r^n\right)\wedge 1\right)\leq C_2r^{m(\sigma d_W/2-d_H/p)}\|f\|_{\Lambda^{p,q}_\sigma(K)}, \end{aligned} \end{align*}$$
where we apply the special case of (a) with one point, one ball and
![]() $\lambda =1$
in the second inequality, and we use the fact that
$\lambda =1$
in the second inequality, and we use the fact that
![]() $\frac {\sigma d_W}{2}>\frac {d_H}{p}$
in the last inequality. Next, we fix
$\frac {\sigma d_W}{2}>\frac {d_H}{p}$
in the last inequality. Next, we fix
![]() $x,y\in K$
such that
$x,y\in K$
such that
![]() $f(x)=\lim _{m\to \infty } E_{B_{r^m}(x)}(f)$
,
$f(x)=\lim _{m\to \infty } E_{B_{r^m}(x)}(f)$
,
![]() $f(y)=\lim _{m\to \infty } E_{B_{r^m}(y)}(f)$
and
$f(y)=\lim _{m\to \infty } E_{B_{r^m}(y)}(f)$
and
![]() $r^{m+1}<R(x,y)\leq r^m$
for some
$r^{m+1}<R(x,y)\leq r^m$
for some
![]() $m\geq 0$
. Choose
$m\geq 0$
. Choose
![]() $k>0$
such that
$k>0$
such that
![]() $r^k<1/2$
and let
$r^k<1/2$
and let
![]() $m'=(m-k)\vee 0$
. It is not hard to see that
$m'=(m-k)\vee 0$
. It is not hard to see that
Combining the above two estimates, we can see that
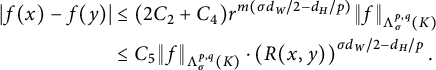 $$\begin{align*}\begin{aligned} |f(x)-f(y)|&\leq (2C_2+C_4)r^{m(\sigma d_W/2-d_H/p)}\|f\|_{\Lambda^{p,q}_\sigma(K)}\\ &\leq C_5\|f\|_{\Lambda^{p,q}_\sigma(K)}\cdot \left(R(x,y)\right)^{\sigma d_W/2-d_H/p}. \end{aligned}\end{align*}$$
$$\begin{align*}\begin{aligned} |f(x)-f(y)|&\leq (2C_2+C_4)r^{m(\sigma d_W/2-d_H/p)}\|f\|_{\Lambda^{p,q}_\sigma(K)}\\ &\leq C_5\|f\|_{\Lambda^{p,q}_\sigma(K)}\cdot \left(R(x,y)\right)^{\sigma d_W/2-d_H/p}. \end{aligned}\end{align*}$$
Since the above estimate holds for
![]() $\mu $
-a.e.
$\mu $
-a.e.
![]() $x,y\in K$
, there exists a Hölder continuous version of f, and the Hölder exponent is
$x,y\in K$
, there exists a Hölder continuous version of f, and the Hölder exponent is
![]() $\sigma d_W/2-d_H/p$
.
$\sigma d_W/2-d_H/p$
.
In addition, we will have a characterization of
![]() $\Lambda ^{p,q}_\sigma (K)$
based on the discrete Laplacian on
$\Lambda ^{p,q}_\sigma (K)$
based on the discrete Laplacian on
![]() $\Lambda _m$
for
$\Lambda _m$
for
![]() $\mathscr {L}_1(p)<\sigma <\mathscr {C}(p)$
.
$\mathscr {L}_1(p)<\sigma <\mathscr {C}(p)$
.
Definition 4.6 (a). For
![]() $m\geq 0$
, define the graph energy form on
$m\geq 0$
, define the graph energy form on
![]() $V_{\Lambda _m}$
by
$V_{\Lambda _m}$
by
(b). Define
![]() $H_{\Lambda _m}: l(V_{\Lambda _m})\to l(V_{\Lambda _m})$
the graph Laplacian associated with
$H_{\Lambda _m}: l(V_{\Lambda _m})\to l(V_{\Lambda _m})$
the graph Laplacian associated with
![]() $\mathcal {E}_{\Lambda _m}$
, i.e.,
$\mathcal {E}_{\Lambda _m}$
, i.e.,
where
![]() $l^2(V_{\Lambda _m})$
stands for the discrete
$l^2(V_{\Lambda _m})$
stands for the discrete
![]() $l^2$
inner product over
$l^2$
inner product over
![]() $V_{\Lambda _m}$
with the counting measure.
$V_{\Lambda _m}$
with the counting measure.
(c). For
![]() $m\geq 1$
, define
$m\geq 1$
, define
![]() $J_m=\left \{f\in C(K): f \text { is harmonic in } F_wK, \forall w\in \Lambda _m, \text { and } f|_{V_{\Lambda _{m-1}}}=0\right \}$
, and call
$J_m=\left \{f\in C(K): f \text { is harmonic in } F_wK, \forall w\in \Lambda _m, \text { and } f|_{V_{\Lambda _{m-1}}}=0\right \}$
, and call
![]() $J_m$
the space of level-m tent functions. For convenience, set
$J_m$
the space of level-m tent functions. For convenience, set
![]() $J_0=\mathcal {H}_0$
.
$J_0=\mathcal {H}_0$
.
(d). For
![]() $1<p<\infty $
,
$1<p<\infty $
,
![]() $1\leq q\leq \infty $
and
$1\leq q\leq \infty $
and
![]() $\sigma>\frac {d_S}{p}$
, define
$\sigma>\frac {d_S}{p}$
, define
with norm
![]() $\|f\|_{\Lambda ^{p,q}_{\sigma ,(1)}(K)}=\|f\|_{L^p(K)}+\big \|r^{m(-\sigma d_W/2+1+d_H/p)}\|H_{\Lambda _m}f\|_{l^p(V_{\Lambda _m})}\big \|_{l^q}$
.
$\|f\|_{\Lambda ^{p,q}_{\sigma ,(1)}(K)}=\|f\|_{L^p(K)}+\big \|r^{m(-\sigma d_W/2+1+d_H/p)}\|H_{\Lambda _m}f\|_{l^p(V_{\Lambda _m})}\big \|_{l^q}$
.
For each
![]() $f\in C(K)$
, clearly f admits a unique expansion in terms of tent functions
$f\in C(K)$
, clearly f admits a unique expansion in terms of tent functions
![]() $f=\sum _{m=0}^\infty f_m$
with
$f=\sum _{m=0}^\infty f_m$
with
![]() $f_m\in J_m,\forall m\geq 0$
.
$f_m\in J_m,\forall m\geq 0$
.
Before proceeding, let’s first collect some easy observations. Recall the notation
![]() $\mathring {V}_{\Lambda _m}$
from Definition 4.1.
$\mathring {V}_{\Lambda _m}$
from Definition 4.1.
Lemma 4.7 Let
![]() $1<p<\infty $
and
$1<p<\infty $
and
![]() $u\in J_m$
with
$u\in J_m$
with
![]() $m\geq 0$
.
$m\geq 0$
.
(a).
![]() $H_{\Lambda _n}u|_{\mathring {V}_{\Lambda _{n}}}=0$
for any
$H_{\Lambda _n}u|_{\mathring {V}_{\Lambda _{n}}}=0$
for any
![]() $n>m$
.
$n>m$
.
(b).
![]() $\|u\|_{L^p(K)}\asymp r^{m(1+d_H/p)}\|H_{\Lambda _m}u\|_{l^p(\mathring {V}_{\Lambda _{m}})}\asymp r^{m(1+d_H/p)}\|H_{\Lambda _m}u\|_{l^p({V}_{\Lambda _{m}})}$
for
$\|u\|_{L^p(K)}\asymp r^{m(1+d_H/p)}\|H_{\Lambda _m}u\|_{l^p(\mathring {V}_{\Lambda _{m}})}\asymp r^{m(1+d_H/p)}\|H_{\Lambda _m}u\|_{l^p({V}_{\Lambda _{m}})}$
for
![]() $m\geq 1$
.
$m\geq 1$
.
(c). For any
![]() $\sigma <\mathscr {C}(p)$
, we have
$\sigma <\mathscr {C}(p)$
, we have
![]() $I_{p}(u,r^n)\leq Cr^{(n-m)\sigma d_W/2}\|u\|_{L^p(K)}$
for all
$I_{p}(u,r^n)\leq Cr^{(n-m)\sigma d_W/2}\|u\|_{L^p(K)}$
for all
![]() $n\geq m$
.
$n\geq m$
.
Proof (a) is trivial since u is harmonic on
![]() $\mathring {V}_{\Lambda _n}$
by definition.
$\mathring {V}_{\Lambda _n}$
by definition.
(b). First, we see the following estimate between
![]() $L^p(K)$
and
$L^p(K)$
and
![]() $l^p(\mathring {V}_{\Lambda _m})$
(or
$l^p(\mathring {V}_{\Lambda _m})$
(or
![]() $l^p(V_{\Lambda _m})$
) norm.
$l^p(V_{\Lambda _m})$
) norm.
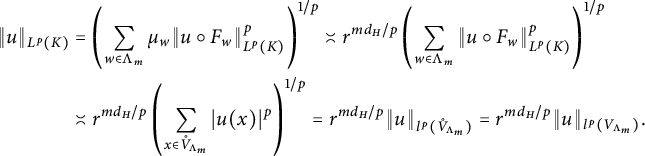 $$\begin{align*}\begin{aligned} \|u\|_{L^p(K)}&=\left(\sum_{w\in \Lambda_{m}}\mu_w\|u\circ F_w\|^p_{L^p(K)}\right)^{1/p}\asymp r^{md_H/p}\left(\sum_{w\in \Lambda_{m}}\|u\circ F_w\|^p_{L^p(K)}\right)^{1/p}\\ &\asymp r^{md_H/p}\left(\sum_{x\in \mathring{V}_{\Lambda_m}}|u(x)|^p\right)^{1/p}=r^{md_H/p}\|u\|_{l^p(\mathring{V}_{\Lambda_m})}=r^{md_H/p}\|u\|_{l^p(V_{\Lambda_m})}. \end{aligned}\end{align*}$$
$$\begin{align*}\begin{aligned} \|u\|_{L^p(K)}&=\left(\sum_{w\in \Lambda_{m}}\mu_w\|u\circ F_w\|^p_{L^p(K)}\right)^{1/p}\asymp r^{md_H/p}\left(\sum_{w\in \Lambda_{m}}\|u\circ F_w\|^p_{L^p(K)}\right)^{1/p}\\ &\asymp r^{md_H/p}\left(\sum_{x\in \mathring{V}_{\Lambda_m}}|u(x)|^p\right)^{1/p}=r^{md_H/p}\|u\|_{l^p(\mathring{V}_{\Lambda_m})}=r^{md_H/p}\|u\|_{l^p(V_{\Lambda_m})}. \end{aligned}\end{align*}$$
To proceed, on one hand, we notice that
![]() $\|H_{\Lambda _m}u\|_{l^p({V}_{\Lambda _{m}})}\lesssim r^{-m}\|u\|_{l^p({V}_{\Lambda _{m}})}$
since
$\|H_{\Lambda _m}u\|_{l^p({V}_{\Lambda _{m}})}\lesssim r^{-m}\|u\|_{l^p({V}_{\Lambda _{m}})}$
since
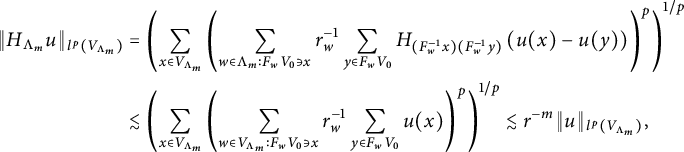 $$\begin{align*}\begin{aligned} \|H_{\Lambda_m}u\|_{l^p(V_{\Lambda_m})}&=\left(\sum_{x\in V_{\Lambda_m}}\left(\sum_{w\in \Lambda_m: F_wV_0\ni x}r_w^{-1}\sum_{y\in F_w V_0} H_{(F_w^{-1}x)(F_w^{-1}y)}\left(u(x)-u(y)\right)\right)^p\right)^{1/p}\\ &\lesssim \left(\sum_{x\in V_{\Lambda_m}}\left(\sum_{w\in V_{\Lambda_m}: F_wV_0\ni x}r_w^{-1}\sum_{y\in F_wV_0}u(x)\right)^p\right)^{1/p}\lesssim r^{-m}\|u\|_{l^p(V_{\Lambda_m})}, \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} \|H_{\Lambda_m}u\|_{l^p(V_{\Lambda_m})}&=\left(\sum_{x\in V_{\Lambda_m}}\left(\sum_{w\in \Lambda_m: F_wV_0\ni x}r_w^{-1}\sum_{y\in F_w V_0} H_{(F_w^{-1}x)(F_w^{-1}y)}\left(u(x)-u(y)\right)\right)^p\right)^{1/p}\\ &\lesssim \left(\sum_{x\in V_{\Lambda_m}}\left(\sum_{w\in V_{\Lambda_m}: F_wV_0\ni x}r_w^{-1}\sum_{y\in F_wV_0}u(x)\right)^p\right)^{1/p}\lesssim r^{-m}\|u\|_{l^p(V_{\Lambda_m})}, \end{aligned} \end{align*}$$
where we recall that
![]() $H=(H_{pq})_{p,q\in V_0}$
is the Laplacian matrix associated with
$H=(H_{pq})_{p,q\in V_0}$
is the Laplacian matrix associated with
![]() ${\mathcal {E}}_0$
. On the other hand, noticing that there are essentially finitely many different types of
${\mathcal {E}}_0$
. On the other hand, noticing that there are essentially finitely many different types of
![]() $F_wK\cap \mathring {V}_{\Lambda _{m}},w\in \Lambda _{m-1}$
, we see that
$F_wK\cap \mathring {V}_{\Lambda _{m}},w\in \Lambda _{m-1}$
, we see that
![]() $\|H_{\Lambda _m}u\|_{l^p(\mathring {V}_{\Lambda _{m}}\cap F_wK)}\asymp r^{-m}\|u\|_{l^p(\mathring {V}_{\Lambda _{m}}\cap F_wK)}$
with “
$\|H_{\Lambda _m}u\|_{l^p(\mathring {V}_{\Lambda _{m}}\cap F_wK)}\asymp r^{-m}\|u\|_{l^p(\mathring {V}_{\Lambda _{m}}\cap F_wK)}$
with “
![]() $\asymp $
” independent of
$\asymp $
” independent of
![]() $w\in \Lambda _{m-1},m\geq 1$
, so by taking summation,
$w\in \Lambda _{m-1},m\geq 1$
, so by taking summation,
(b) follows by combining the above three estimates.
(c). For
![]() $m=0$
, the result trivially follows from the definition of
$m=0$
, the result trivially follows from the definition of
![]() $\mathscr C(p)$
. It suffices to consider
$\mathscr C(p)$
. It suffices to consider
![]() $m\geq 1$
case. Choose k such that
$m\geq 1$
case. Choose k such that
![]() $R(x,y)>r^{k+n}$
for any
$R(x,y)>r^{k+n}$
for any
![]() $x,y$
not in adjacent cells in
$x,y$
not in adjacent cells in
![]() $\{F_{\tau } K: {\tau }\in \Lambda _n\}$
and for any
$\{F_{\tau } K: {\tau }\in \Lambda _n\}$
and for any
![]() $n\geq 0$
. Now, for any fixed
$n\geq 0$
. Now, for any fixed
![]() $w\in \Lambda _m$
, we consider the integral
$w\in \Lambda _m$
, we consider the integral
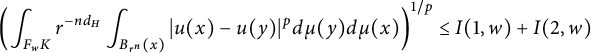 $$\begin{align*}\left(\int_{F_wK}r^{-nd_H}\int_{B_{r^{n}}(x)}|u(x)-u(y)|^pd\mu(y)d\mu(x)\right)^{1/p}\leq I(1,w)+I(2,w)\end{align*}$$
$$\begin{align*}\left(\int_{F_wK}r^{-nd_H}\int_{B_{r^{n}}(x)}|u(x)-u(y)|^pd\mu(y)d\mu(x)\right)^{1/p}\leq I(1,w)+I(2,w)\end{align*}$$
with
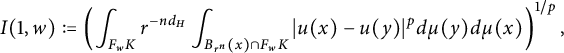 $$\begin{align*}I(1,w):=\left(\int_{F_wK}r^{-nd_H}\int_{B_{r^{n}}(x)\cap F_wK}|u(x)-u(y)|^pd\mu(y)d\mu(x)\right)^{1/p},\end{align*}$$
$$\begin{align*}I(1,w):=\left(\int_{F_wK}r^{-nd_H}\int_{B_{r^{n}}(x)\cap F_wK}|u(x)-u(y)|^pd\mu(y)d\mu(x)\right)^{1/p},\end{align*}$$
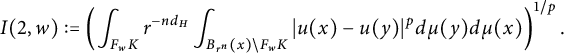 $$\begin{align*}I(2,w):=\left(\int_{F_wK}r^{-nd_H}\int_{B_{r^{n}}(x)\setminus F_wK}|u(x)-u(y)|^pd\mu(y)d\mu(x)\right)^{1/p}.\end{align*}$$
$$\begin{align*}I(2,w):=\left(\int_{F_wK}r^{-nd_H}\int_{B_{r^{n}}(x)\setminus F_wK}|u(x)-u(y)|^pd\mu(y)d\mu(x)\right)^{1/p}.\end{align*}$$
Notice that
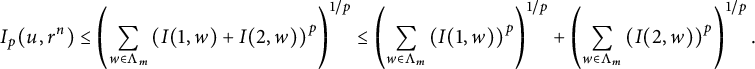 $$\begin{align*}I_p(u,r^n)\leq \left(\sum_{w\in \Lambda_m}\left(I(1,w)+I(2,w)\right)^p\right)^{1/p}\leq \left(\sum_{w\in \Lambda_m}\left(I(1,w)\right)^p\right)^{1/p}+\left(\sum_{w\in \Lambda_m}\left(I(2,w)\right)^p\right)^{1/p}.\end{align*}$$
$$\begin{align*}I_p(u,r^n)\leq \left(\sum_{w\in \Lambda_m}\left(I(1,w)+I(2,w)\right)^p\right)^{1/p}\leq \left(\sum_{w\in \Lambda_m}\left(I(1,w)\right)^p\right)^{1/p}+\left(\sum_{w\in \Lambda_m}\left(I(2,w)\right)^p\right)^{1/p}.\end{align*}$$
Let’s estimate
![]() $I(1,w)$
and
$I(1,w)$
and
![]() $I(2,w)$
. For
$I(2,w)$
. For
![]() $I(1,w)$
, we notice that
$I(1,w)$
, we notice that
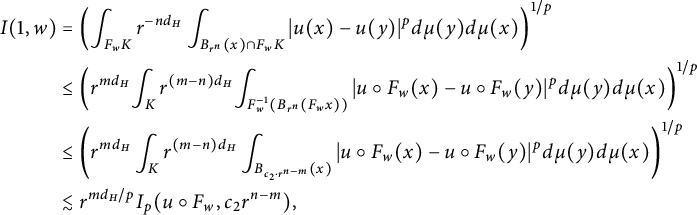 $$\begin{align*}\begin{aligned} I(1,w)&=\left(\int_{F_wK}r^{-nd_H}\int_{B_{r^{n}}(x)\cap F_wK}|u(x)-u(y)|^pd\mu(y)d\mu(x)\right)^{1/p}\\&\leq \left(r^{md_H}\!\int_{K}r^{(m-n)d_H}\!\int_{F_w^{-1}\left(B_{r^{n}}(F_wx)\right)}|u\circ F_w(x)-u\circ F_w(y)|^pd\mu(y)d\mu(x)\right)^{1/p}\\&\leq \left(r^{md_H}\int_{K}r^{(m-n)d_H}\int_{B_{c_2\cdot r^{n-m}}(x)}|u\circ F_w(x)-u\circ F_w(y)|^pd\mu(y)d\mu(x)\right)^{1/p}\\ &\lesssim r^{md_H/p}I_p(u\circ F_w,c_2r^{n-m}), \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} I(1,w)&=\left(\int_{F_wK}r^{-nd_H}\int_{B_{r^{n}}(x)\cap F_wK}|u(x)-u(y)|^pd\mu(y)d\mu(x)\right)^{1/p}\\&\leq \left(r^{md_H}\!\int_{K}r^{(m-n)d_H}\!\int_{F_w^{-1}\left(B_{r^{n}}(F_wx)\right)}|u\circ F_w(x)-u\circ F_w(y)|^pd\mu(y)d\mu(x)\right)^{1/p}\\&\leq \left(r^{md_H}\int_{K}r^{(m-n)d_H}\int_{B_{c_2\cdot r^{n-m}}(x)}|u\circ F_w(x)-u\circ F_w(y)|^pd\mu(y)d\mu(x)\right)^{1/p}\\ &\lesssim r^{md_H/p}I_p(u\circ F_w,c_2r^{n-m}), \end{aligned} \end{align*}$$
where
![]() $c_2$
is constant depending only on K and the harmonic structure, noticing that there is
$c_2$
is constant depending only on K and the harmonic structure, noticing that there is
![]() $c_1\in (0,1)$
such that
$c_1\in (0,1)$
such that
![]() $R(F_wx,F_wy)\geq c_1r_wR(x,y),\forall w\in W_*,x,y\in K$
. In addition, since
$R(F_wx,F_wy)\geq c_1r_wR(x,y),\forall w\in W_*,x,y\in K$
. In addition, since
![]() $u\circ F_w\in \mathcal {H}_0$
and
$u\circ F_w\in \mathcal {H}_0$
and
![]() $\sigma <\mathscr {C}(p)$
, we know that
$\sigma <\mathscr {C}(p)$
, we know that
where the second inequality is due to the fact that all norms on the finite dimensional space
![]() $\mathcal {H}_0$
are equivalent. Combining the above two observations, we get
$\mathcal {H}_0$
are equivalent. Combining the above two observations, we get
For
![]() $I(2,w)$
, we can see that in fact
$I(2,w)$
, we can see that in fact
![]() $B_{r^n}(x)\setminus F_wK\neq \emptyset $
only if x stays in a cell
$B_{r^n}(x)\setminus F_wK\neq \emptyset $
only if x stays in a cell
![]() $F_\tau K$
with
$F_\tau K$
with
![]() $\tau \in \Lambda _{n-k}$
which contains a point
$\tau \in \Lambda _{n-k}$
which contains a point
![]() $z\in F_wV_0$
. Without loss of generality, we assume that
$z\in F_wV_0$
. Without loss of generality, we assume that
![]() $n-k\geq m$
, and sum
$n-k\geq m$
, and sum
![]() $I(2,w)$
’s over
$I(2,w)$
’s over
![]() $\Lambda _m$
to get
$\Lambda _m$
to get
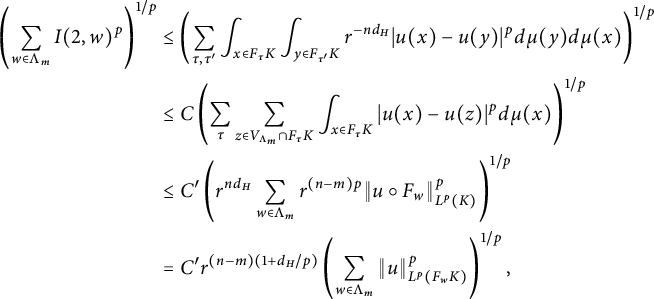 $$\begin{align*}\begin{aligned} \left(\sum_{w\in\Lambda_m} I(2,w)^p\right)^{1/p}&\leq \left(\sum_{\tau,\tau'}\int_{x\in F_\tau K}\int_{y\in F_{\tau'}K}r^{-nd_H}|u(x)-u(y)|^pd\mu(y)d\mu(x)\right)^{1/p}\\ &\leq C\left(\sum_{\tau}\sum_{z\in V_{\Lambda_m}\cap F_\tau K}\int_{x\in F_\tau K}|u(x)-u(z)|^pd\mu(x)\right)^{1/p}\\ &\leq C'\left(r^{nd_H}\sum_{w \in \Lambda_m} r^{(n-m)p}\|u\circ F_w\|^p_{L^p(K)}\right)^{1/p}\\ &=C'r^{(n-m)(1+d_H/p)}\left(\sum_{w \in \Lambda_m}\|u\|^p_{L^p(F_wK)}\right)^{1/p}, \end{aligned}\end{align*}$$
$$\begin{align*}\begin{aligned} \left(\sum_{w\in\Lambda_m} I(2,w)^p\right)^{1/p}&\leq \left(\sum_{\tau,\tau'}\int_{x\in F_\tau K}\int_{y\in F_{\tau'}K}r^{-nd_H}|u(x)-u(y)|^pd\mu(y)d\mu(x)\right)^{1/p}\\ &\leq C\left(\sum_{\tau}\sum_{z\in V_{\Lambda_m}\cap F_\tau K}\int_{x\in F_\tau K}|u(x)-u(z)|^pd\mu(x)\right)^{1/p}\\ &\leq C'\left(r^{nd_H}\sum_{w \in \Lambda_m} r^{(n-m)p}\|u\circ F_w\|^p_{L^p(K)}\right)^{1/p}\\ &=C'r^{(n-m)(1+d_H/p)}\left(\sum_{w \in \Lambda_m}\|u\|^p_{L^p(F_wK)}\right)^{1/p}, \end{aligned}\end{align*}$$
where
![]() $\tau ,\tau '\in \{\tau "\in \Lambda _{n-k}:F_{\tau "}K\cap V_{\Lambda _m}\neq \emptyset \}$
, and we require
$\tau ,\tau '\in \{\tau "\in \Lambda _{n-k}:F_{\tau "}K\cap V_{\Lambda _m}\neq \emptyset \}$
, and we require
![]() $\tau \neq \tau '$
with
$\tau \neq \tau '$
with
![]() $F_\tau K\cap F_{\tau '} K\neq \emptyset $
in the first line.
$F_\tau K\cap F_{\tau '} K\neq \emptyset $
in the first line.
Combining the estimates on
![]() $I(1,w)$
’s and
$I(1,w)$
’s and
![]() $I(2,w)$
’s, and noticing that
$I(2,w)$
’s, and noticing that
by Proposition 3.3, (c) follows.
Now, we state the main result in this subsection.
Theorem 4.8 Let
![]() $f\in C(K)$
with
$f\in C(K)$
with
![]() $f=\sum _{m=0}^\infty f_m$
and
$f=\sum _{m=0}^\infty f_m$
and
![]() $f_m\in J_m,\forall m\geq 0$
. For
$f_m\in J_m,\forall m\geq 0$
. For
![]() $1<p<\infty $
,
$1<p<\infty $
,
![]() $1\leq q\leq \infty $
, for the claims:
$1\leq q\leq \infty $
, for the claims:
![]() $(1)\text { }f\in \Lambda ^{p,q}_\sigma (K)$
;
$(1)\text { }f\in \Lambda ^{p,q}_\sigma (K)$
;
![]() $(2)\text { }f\in \Lambda ^{p,q}_{\sigma ,(1)}(K)$
;
$(2)\text { }f\in \Lambda ^{p,q}_{\sigma ,(1)}(K)$
;
![]() $(3)\text { }\left \{r^{-m\sigma d_W/2}\|f_m\|_{L^p(K)}\right \}_{m\geq 0}\in l^q$
,
$(3)\text { }\left \{r^{-m\sigma d_W/2}\|f_m\|_{L^p(K)}\right \}_{m\geq 0}\in l^q$
,
we can say:
(a). If
![]() $\sigma>\mathscr {L}_1(p)$
, we have
$\sigma>\mathscr {L}_1(p)$
, we have
![]() $(1)\Longrightarrow (2)\Longrightarrow (3)$
with
$(1)\Longrightarrow (2)\Longrightarrow (3)$
with
(b). If
![]() $\mathscr {L}_1(p)<\sigma <\mathscr {L}_2(p)$
, we have
$\mathscr {L}_1(p)<\sigma <\mathscr {L}_2(p)$
, we have
![]() $(1)\Longrightarrow (2)\iff (3)$
with
$(1)\Longrightarrow (2)\iff (3)$
with
(c). If
![]() $(\frac {1}{p},\sigma )\in \mathscr {A}_1$
, we have
$(\frac {1}{p},\sigma )\in \mathscr {A}_1$
, we have
![]() $(1)\iff (2)\iff (3)$
with
$(1)\iff (2)\iff (3)$
with
Proof (a). We first prove
![]() $(1)\Longrightarrow (2)$
. We follow the conventional notation to denote
$(1)\Longrightarrow (2)$
. We follow the conventional notation to denote
![]() $x\sim _m y$
if
$x\sim _m y$
if
![]() $x,y\in F_wV_0$
for some
$x,y\in F_wV_0$
for some
![]() $w\in \Lambda _m$
. We fix
$w\in \Lambda _m$
. We fix
![]() $k>0$
so that
$k>0$
so that
![]() $B_{r^m}(y)\subset B_{r^{m-k}}(x)$
for any
$B_{r^m}(y)\subset B_{r^{m-k}}(x)$
for any
![]() $x\sim _m y$
and
$x\sim _m y$
and
![]() $m\geq 0$
. Then we can see
$m\geq 0$
. Then we can see
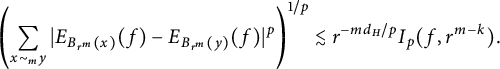 $$\begin{align*}\left(\sum_{x\sim_m y}|E_{B_{r^m}(x)}(f)-E_{B_{r^m}(y)}(f)|^p\right)^{1/p}\lesssim r^{-md_H/p}I_p(f,r^{m-k}).\end{align*}$$
$$\begin{align*}\left(\sum_{x\sim_m y}|E_{B_{r^m}(x)}(f)-E_{B_{r^m}(y)}(f)|^p\right)^{1/p}\lesssim r^{-md_H/p}I_p(f,r^{m-k}).\end{align*}$$
Since each vertex
![]() $x\in V_{\Lambda _m}$
is of bounded degree, by writing
$x\in V_{\Lambda _m}$
is of bounded degree, by writing
we apply Lemma 4.5(a) to see that
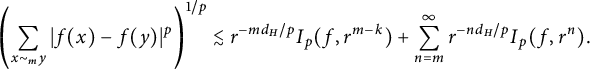 $$\begin{align*}\left(\sum_{x\sim_m y}|f(x)-f(y)|^p\right)^{1/p}\lesssim r^{-md_H/p}I_p(f,r^{m-k})+\sum_{n=m}^\infty r^{-nd_H/p}I_p(f,r^n).\end{align*}$$
$$\begin{align*}\left(\sum_{x\sim_m y}|f(x)-f(y)|^p\right)^{1/p}\lesssim r^{-md_H/p}I_p(f,r^{m-k})+\sum_{n=m}^\infty r^{-nd_H/p}I_p(f,r^n).\end{align*}$$
Write
![]() $\tilde {H}_{\Lambda _m}f=r^{m(1+d_H/p)}H_{\Lambda _m}f$
for convenience. We then have
$\tilde {H}_{\Lambda _m}f=r^{m(1+d_H/p)}H_{\Lambda _m}f$
for convenience. We then have
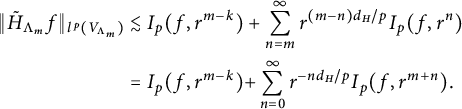 $$\begin{align*}\begin{aligned} \|\tilde{H}_{\Lambda_m}f\|_{l^p(V_{\Lambda_m})}&\lesssim I_p(f,r^{m-k})+\sum_{n=m}^\infty r^{(m-n)d_H/p}I_p(f,r^n)\\ &= {I_p(f,r^{m-k})+}\sum_{n=0}^\infty r^{-nd_H/p}I_p(f,r^{m+n}). \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} \|\tilde{H}_{\Lambda_m}f\|_{l^p(V_{\Lambda_m})}&\lesssim I_p(f,r^{m-k})+\sum_{n=m}^\infty r^{(m-n)d_H/p}I_p(f,r^n)\\ &= {I_p(f,r^{m-k})+}\sum_{n=0}^\infty r^{-nd_H/p}I_p(f,r^{m+n}). \end{aligned} \end{align*}$$
Noticing that
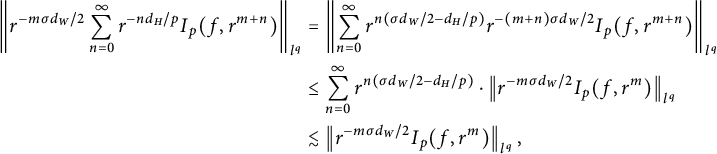 $$\begin{align*}\begin{aligned} \left\|r^{-m\sigma d_W/2}\sum_{n=0}^\infty r^{-nd_H/p}I_p(f,r^{m+n})\right\|_{l^q}&=\left\|\sum_{n=0}^\infty r^{n(\sigma d_W/2-d_H/p)}r^{-(m+n)\sigma d_W/2}I_p(f,r^{m+n})\right\|_{l^q}\\ &\leq \sum_{n=0}^\infty r^{n(\sigma d_W/2-d_H/p)}\cdot\left\|r^{-m\sigma d_W/2}I_p(f,r^{m})\right\|_{l^q}\\ &\lesssim \left\|r^{-m\sigma d_W/2}I_p(f,r^{m})\right\|_{l^q}, \end{aligned}\end{align*}$$
$$\begin{align*}\begin{aligned} \left\|r^{-m\sigma d_W/2}\sum_{n=0}^\infty r^{-nd_H/p}I_p(f,r^{m+n})\right\|_{l^q}&=\left\|\sum_{n=0}^\infty r^{n(\sigma d_W/2-d_H/p)}r^{-(m+n)\sigma d_W/2}I_p(f,r^{m+n})\right\|_{l^q}\\ &\leq \sum_{n=0}^\infty r^{n(\sigma d_W/2-d_H/p)}\cdot\left\|r^{-m\sigma d_W/2}I_p(f,r^{m})\right\|_{l^q}\\ &\lesssim \left\|r^{-m\sigma d_W/2}I_p(f,r^{m})\right\|_{l^q}, \end{aligned}\end{align*}$$
since we assume
![]() $\sigma>\mathscr {L}_1(p)=\frac {d_S}{p}$
, the claim follows.
$\sigma>\mathscr {L}_1(p)=\frac {d_S}{p}$
, the claim follows.
![]() $(2)\Longrightarrow (3)$
is easy. We can see that
$(2)\Longrightarrow (3)$
is easy. We can see that
![]() $H_{\Lambda _m}\left (\sum _{n=0}^{m-1}f_m\right )|_{\mathring {V}_{\Lambda _m}}\equiv 0$
by Lemma 4.7(a), and
$H_{\Lambda _m}\left (\sum _{n=0}^{m-1}f_m\right )|_{\mathring {V}_{\Lambda _m}}\equiv 0$
by Lemma 4.7(a), and
![]() $(\sum _{n=0}^m f_m)|_{V_{\Lambda _m}}=f|_{V_{\Lambda _m}}$
. Thus,
$(\sum _{n=0}^m f_m)|_{V_{\Lambda _m}}=f|_{V_{\Lambda _m}}$
. Thus,
![]() $H_{\Lambda _m }f|_{\mathring {V}_{\Lambda _m}}=H_{\Lambda _m}f_m|_{\mathring {V}_{\Lambda _m}}$
and then
$H_{\Lambda _m }f|_{\mathring {V}_{\Lambda _m}}=H_{\Lambda _m}f_m|_{\mathring {V}_{\Lambda _m}}$
and then
using Lemma 4.7(b). The claim follows immediately.
(b). It remains to show
![]() $(3)\Longrightarrow (2)$
. By the definition of
$(3)\Longrightarrow (2)$
. By the definition of
![]() $\mathcal {E}_{\Lambda _m}$
and the fact that
$\mathcal {E}_{\Lambda _m}$
and the fact that
![]() $f_m$
is harmonic in
$f_m$
is harmonic in
![]() $F_wK$
for each
$F_wK$
for each
![]() $w\in \Lambda _m$
, we can see that
$w\in \Lambda _m$
, we can see that
Also,
![]() $\|H_{\Lambda _n}f_m\|_{l^p(V_{\Lambda _n})}=0$
for
$\|H_{\Lambda _n}f_m\|_{l^p(V_{\Lambda _n})}=0$
for
![]() $n<m$
. Thus,
$n<m$
. Thus,
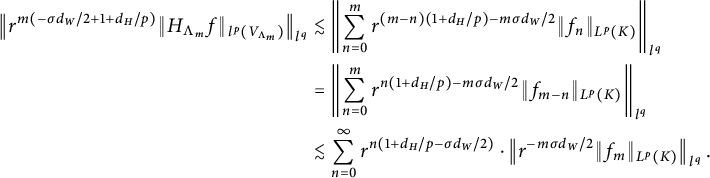 $$\begin{align*}\begin{aligned} \left\|r^{m(-\sigma d_W/2+1+d_H/p)}\|H_{\Lambda_m}f\|_{l^p(V_{\Lambda_m})}\right\|_{l^q}&\lesssim \left\|\sum_{n=0}^mr^{(m-n)(1+d_H/p)-m\sigma d_W/2}\|f_n\|_{L^p(K)}\right\|_{l^q}\\ &=\left\|\sum_{n=0}^mr^{n(1+d_H/p)-m\sigma d_W/2}\|f_{m-n}\|_{L^p(K)}\right\|_{l^q}\\ &\lesssim \sum_{n=0}^\infty r^{n(1+d_H/p-\sigma d_W/2)}\cdot\left\|r^{-m\sigma d_W/2}\|f_m\|_{L^p(K)}\right\|_{l^q}. \end{aligned}\end{align*}$$
$$\begin{align*}\begin{aligned} \left\|r^{m(-\sigma d_W/2+1+d_H/p)}\|H_{\Lambda_m}f\|_{l^p(V_{\Lambda_m})}\right\|_{l^q}&\lesssim \left\|\sum_{n=0}^mr^{(m-n)(1+d_H/p)-m\sigma d_W/2}\|f_n\|_{L^p(K)}\right\|_{l^q}\\ &=\left\|\sum_{n=0}^mr^{n(1+d_H/p)-m\sigma d_W/2}\|f_{m-n}\|_{L^p(K)}\right\|_{l^q}\\ &\lesssim \sum_{n=0}^\infty r^{n(1+d_H/p-\sigma d_W/2)}\cdot\left\|r^{-m\sigma d_W/2}\|f_m\|_{L^p(K)}\right\|_{l^q}. \end{aligned}\end{align*}$$
The claim follows since
![]() $1+\frac {d_H}{p}-\frac {\sigma d_W}{2}>0$
by
$1+\frac {d_H}{p}-\frac {\sigma d_W}{2}>0$
by
![]() $\sigma <\mathscr L_2(p)$
.
$\sigma <\mathscr L_2(p)$
.
(c). We only need to prove
![]() $(3)\Longrightarrow (1)$
. Since
$(3)\Longrightarrow (1)$
. Since
![]() $(\frac {1}{p},\sigma )\in \mathscr {A}_1$
, which means that we have
$(\frac {1}{p},\sigma )\in \mathscr {A}_1$
, which means that we have
![]() $\sigma <\mathscr {C}(p)$
in addition to
$\sigma <\mathscr {C}(p)$
in addition to
![]() $\mathscr {L}_1(p)<\sigma <\mathscr {L}_2(p)$
, we can find
$\mathscr {L}_1(p)<\sigma <\mathscr {L}_2(p)$
, we can find
![]() $\eta \in (\sigma ,\mathscr {C}(p))$
. The rest proof goes similar to the second part of Proposition 4.4. By using Lemma 4.7(c), we can see
$\eta \in (\sigma ,\mathscr {C}(p))$
. The rest proof goes similar to the second part of Proposition 4.4. By using Lemma 4.7(c), we can see
Then, by the proof of (4.5), we get
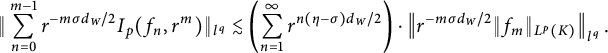 $$\begin{align*}\|\sum_{n=0}^{m-1} r^{-m\sigma d_W/2}I_p(f_n,r^m)\|_{l^q}\lesssim \left(\sum_{n=1}^\infty r^{n(\eta-\sigma)d_W/2}\right)\cdot \left\|r^{-m\sigma d_W/2}\|f_m\|_{L^p(K)}\right\|_{l^q}. \end{align*}$$
$$\begin{align*}\|\sum_{n=0}^{m-1} r^{-m\sigma d_W/2}I_p(f_n,r^m)\|_{l^q}\lesssim \left(\sum_{n=1}^\infty r^{n(\eta-\sigma)d_W/2}\right)\cdot \left\|r^{-m\sigma d_W/2}\|f_m\|_{L^p(K)}\right\|_{l^q}. \end{align*}$$
In addition, by Lemma 4.3(c) and the same proof of (4.6), we have
The claim then follows by combining the above two estimates, and noticing that
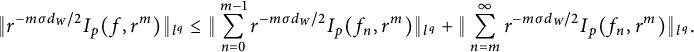 $$\begin{align*}\|r^{-m\sigma d_W/2}I_p(f,r^m)\|_{l^q}\leq \|\sum_{n=0}^{m-1} r^{-m\sigma d_W/2}I_p(f_n,r^m)\|_{l^q}+\|\sum_{n=m}^{\infty} r^{-m\sigma d_W/2}I_p(f_n,r^m)\|_{l^q}.\end{align*}$$
$$\begin{align*}\|r^{-m\sigma d_W/2}I_p(f,r^m)\|_{l^q}\leq \|\sum_{n=0}^{m-1} r^{-m\sigma d_W/2}I_p(f_n,r^m)\|_{l^q}+\|\sum_{n=m}^{\infty} r^{-m\sigma d_W/2}I_p(f_n,r^m)\|_{l^q}.\end{align*}$$
We end this section with the following theorem, whose proof will be completed in Section 5 and Section 6.
Theorem 4.9 For
![]() $1<p<\infty $
,
$1<p<\infty $
,
![]() $1\leq q\leq \infty $
and
$1\leq q\leq \infty $
and
![]() $\mathscr {L}_1(p)<\sigma <2$
, we have
$\mathscr {L}_1(p)<\sigma <2$
, we have
![]() $B^{p,q}_\sigma (K)=\Lambda ^{p,q}_{\sigma ,(1)}(K)$
with
$B^{p,q}_\sigma (K)=\Lambda ^{p,q}_{\sigma ,(1)}(K)$
with
![]() $\|\cdot \|_{\Lambda ^{p,q}_{\sigma ,(1)}(K)}\asymp \|\cdot \|_{B^{p,q}_\sigma (K)}$
.
$\|\cdot \|_{\Lambda ^{p,q}_{\sigma ,(1)}(K)}\asymp \|\cdot \|_{B^{p,q}_\sigma (K)}$
.
5 Embedding
 $\Lambda ^{p,q}_\sigma (K)$
into
$\Lambda ^{p,q}_\sigma (K)$
into
 $B^{p,q}_\sigma (K)$
$B^{p,q}_\sigma (K)$
In this section, we will use the J-method of real interpolation to prove that
![]() $\Lambda ^{p,q}_\sigma (K)\subset B^{p,q}_\sigma (K)$
for
$\Lambda ^{p,q}_\sigma (K)\subset B^{p,q}_\sigma (K)$
for
![]() $0<\sigma <2$
. This will not involve the critical curve
$0<\sigma <2$
. This will not involve the critical curve
![]() $\mathscr {C}$
.
$\mathscr {C}$
.
We will use the following fact about the real interpolation, which is obvious from the J-method. Readers may find details of the J-method in the book [Reference Bergh and Löfström9].
Lemma 5.1 Let
![]() $\bar {X}:=(X_0,X_1)$
be an interpolation couple of Banach spaces,
$\bar {X}:=(X_0,X_1)$
be an interpolation couple of Banach spaces,
![]() $1\leq q\leq \infty $
,
$1\leq q\leq \infty $
,
![]() $0<\theta <1$
, and
$0<\theta <1$
, and
![]() $\bar {X}_{\theta ,q}:=(X_0,X_1)_{\theta ,q}$
be the real interpolation space. For each
$\bar {X}_{\theta ,q}:=(X_0,X_1)_{\theta ,q}$
be the real interpolation space. For each
![]() $x\in X_0\cap X_1$
and
$x\in X_0\cap X_1$
and
![]() $\lambda>0$
, write
$\lambda>0$
, write
If
![]() $\{g_m\}_{m\geq 0}\subset X_0\cap X_1$
is a sequence with
$\{g_m\}_{m\geq 0}\subset X_0\cap X_1$
is a sequence with
![]() $\left \{\lambda ^{-m\theta }J(\lambda ^{m},g_m)\right \}_{m\geq 0}\in l^q$
and
$\left \{\lambda ^{-m\theta }J(\lambda ^{m},g_m)\right \}_{m\geq 0}\in l^q$
and
![]() $\lambda>0$
, then
$\lambda>0$
, then
with
![]() $\|g\|_{\bar {X}_{\theta ,q}}\lesssim \big \|\lambda ^{-m\theta }J(\lambda ^{m},g_m)\big \|_{l^q}$
.
$\|g\|_{\bar {X}_{\theta ,q}}\lesssim \big \|\lambda ^{-m\theta }J(\lambda ^{m},g_m)\big \|_{l^q}$
.
We start with the following lemma.
Lemma 5.2 For
![]() $1<p<\infty $
,
$1<p<\infty $
,
![]() $f\in L^p(K)$
and
$f\in L^p(K)$
and
![]() $m\geq 0$
, there is a function
$m\geq 0$
, there is a function
![]() $u_m$
in
$u_m$
in
![]() $H^p_2(K)$
such that
$H^p_2(K)$
such that
and in addition,
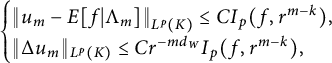 $$\begin{align*}\begin{cases} \left\|u_m-E[f|\Lambda_m]\right\|_{L^p(K)}\leq CI_{p}(f,r^{m-k}),\\ \|\Delta u_m\|_{L^p(K)}\leq Cr^{-md_W}I_{p}(f,r^{m-k}), \end{cases}\end{align*}$$
$$\begin{align*}\begin{cases} \left\|u_m-E[f|\Lambda_m]\right\|_{L^p(K)}\leq CI_{p}(f,r^{m-k}),\\ \|\Delta u_m\|_{L^p(K)}\leq Cr^{-md_W}I_{p}(f,r^{m-k}), \end{cases}\end{align*}$$
where
![]() $k\in \mathbb {N}$
and
$k\in \mathbb {N}$
and
![]() $C>0$
are constants independent of f and m.
$C>0$
are constants independent of f and m.
Proof For convenience, we write
![]() $E[f|\Lambda _m]=\sum _{w\in \Lambda _m} c_w1_{F_wK}$
with
$E[f|\Lambda _m]=\sum _{w\in \Lambda _m} c_w1_{F_wK}$
with
![]() $c_w\in \mathbb {C}$
.
$c_w\in \mathbb {C}$
.
For each
![]() $x\in V_{\Lambda _m}$
and
$x\in V_{\Lambda _m}$
and
![]() $n\geq m$
, we write
$n\geq m$
, we write
![]() $U_{x,n}=\bigcup \{F_{w'}K: x\in F_{w'}K, w'\in \Lambda _{n}\}$
, and take
$U_{x,n}=\bigcup \{F_{w'}K: x\in F_{w'}K, w'\in \Lambda _{n}\}$
, and take
![]() $m'\geq m$
to be the smallest one, such that
$m'\geq m$
to be the smallest one, such that
Clearly, the difference
![]() $m'-m$
is bounded for all m.
$m'-m$
is bounded for all m.
Let
![]() $U_{m'}=\bigcup _{x\in V_{\Lambda _m}}U_{x,m'}$
. We define
$U_{m'}=\bigcup _{x\in V_{\Lambda _m}}U_{x,m'}$
. We define
![]() $u_m$
as follows:
$u_m$
as follows:
(1). For
![]() $x\in K\setminus U_{m'}$
, we define
$x\in K\setminus U_{m'}$
, we define
![]() $u_m(x)=E[f|\Lambda _m](x)$
.
$u_m(x)=E[f|\Lambda _m](x)$
.
(2). For
![]() $x\in V_{\Lambda _m}$
, we let
$x\in V_{\Lambda _m}$
, we let
![]() $M_x=\#\{w\in \Lambda _m:x\in F_wK\}$
and define
$M_x=\#\{w\in \Lambda _m:x\in F_wK\}$
and define
(3). It remains to construct
![]() $u_m$
on each
$u_m$
on each
![]() $U_{x,m'}$
with
$U_{x,m'}$
with
![]() $x\in V_{\Lambda _m}$
. In this case, for each
$x\in V_{\Lambda _m}$
. In this case, for each
![]() $F_{w'}K\subset U_{x,m'}$
with
$F_{w'}K\subset U_{x,m'}$
with
![]() $w'\in \Lambda _{m'}$
, we have already defined its boundary values. For
$w'\in \Lambda _{m'}$
, we have already defined its boundary values. For
![]() $u_m$
in
$u_m$
in
![]() $F_{w'}K$
, additionally, we require that
$F_{w'}K$
, additionally, we require that
![]() $u_m$
satisfies the Neumann boundary condition on
$u_m$
satisfies the Neumann boundary condition on
![]() $F_{w'}V_0$
, and
$F_{w'}V_0$
, and
![]() $E_{w'}(u_m)=c_w$
for w to be the word in
$E_{w'}(u_m)=c_w$
for w to be the word in
![]() $\Lambda _m$
such that
$\Lambda _m$
such that
![]() $F_{w'}K\subset F_wK$
. It is easy to see the existence of such a function locally on
$F_{w'}K\subset F_wK$
. It is easy to see the existence of such a function locally on
![]() $F_{w'}K$
, and the following estimate can be achieved by scaling:
$F_{w'}K$
, and the following estimate can be achieved by scaling:
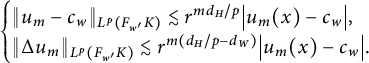 $$\begin{align*}\begin{cases} \|u_m-c_w\|_{L^p(F_{w'}K)}\lesssim r^{md_H/p}\big|u_m(x)-c_w\big|,\\ \|\Delta u_m\|_{L^p(F_{w'}K)}\lesssim r^{m(d_H/p-d_W)}\big|u_m(x)-c_w\big|. \end{cases}\end{align*}$$
$$\begin{align*}\begin{cases} \|u_m-c_w\|_{L^p(F_{w'}K)}\lesssim r^{md_H/p}\big|u_m(x)-c_w\big|,\\ \|\Delta u_m\|_{L^p(F_{w'}K)}\lesssim r^{m(d_H/p-d_W)}\big|u_m(x)-c_w\big|. \end{cases}\end{align*}$$
With (1)–(3), we obtain a function
![]() $u_m\in H^p_2(K)$
such that
$u_m\in H^p_2(K)$
such that
![]() $E[u_m|\Lambda _m]=E[f|\Lambda _m]$
. It remains to show the desired estimates for
$E[u_m|\Lambda _m]=E[f|\Lambda _m]$
. It remains to show the desired estimates for
![]() $u_m$
. First, we have
$u_m$
. First, we have
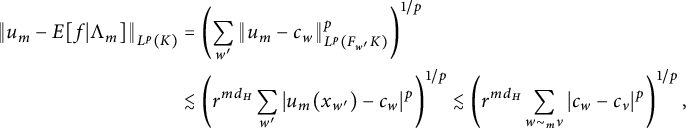 $$\begin{align*}\begin{aligned} \left\|u_m-E[f|\Lambda_m]\right\|_{L^p(K)}&=\left(\sum_{w'}\|u_m-c_w\|^p_{L^p(F_{w'}K)}\right)^{1/p}\\ &\lesssim \left(r^{md_H}\sum_{w'}|u_m(x_{w'})-c_w|^p\right)^{1/p} \lesssim \left(r^{md_H}\sum_{w\sim_m \nu}|c_w-c_\nu|^p\right)^{1/p}, \end{aligned}\end{align*}$$
$$\begin{align*}\begin{aligned} \left\|u_m-E[f|\Lambda_m]\right\|_{L^p(K)}&=\left(\sum_{w'}\|u_m-c_w\|^p_{L^p(F_{w'}K)}\right)^{1/p}\\ &\lesssim \left(r^{md_H}\sum_{w'}|u_m(x_{w'})-c_w|^p\right)^{1/p} \lesssim \left(r^{md_H}\sum_{w\sim_m \nu}|c_w-c_\nu|^p\right)^{1/p}, \end{aligned}\end{align*}$$
where the summation
![]() $\sum _{w'}$
is over all
$\sum _{w'}$
is over all
![]() $w'\in \Lambda _{m'}$
such that
$w'\in \Lambda _{m'}$
such that
![]() $F_{w'}K\cap V_{\Lambda _{m}}\neq \emptyset $
and
$F_{w'}K\cap V_{\Lambda _{m}}\neq \emptyset $
and
![]() $x_{w'}$
is the single vertex in
$x_{w'}$
is the single vertex in
![]() $F_{w'}K\cap V_{\Lambda _m}$
, w stands for the word in
$F_{w'}K\cap V_{\Lambda _m}$
, w stands for the word in
![]() $\Lambda _m$
such that
$\Lambda _m$
such that
![]() $F_{w'}K\subset F_{w}K$
, and
$F_{w'}K\subset F_{w}K$
, and
![]() $\sum _{w\sim _m\nu }$
is over all the pairs
$\sum _{w\sim _m\nu }$
is over all the pairs
![]() $w,\nu \in \Lambda _m$
with
$w,\nu \in \Lambda _m$
with
![]() $F_wK\cap F_\nu K\neq \emptyset $
. By choosing
$F_wK\cap F_\nu K\neq \emptyset $
. By choosing
![]() $k\in \mathbb {N}$
such that
$k\in \mathbb {N}$
such that
![]() $r^{m-k}>2{\mathrm {diam}} F_wK$
for any
$r^{m-k}>2{\mathrm {diam}} F_wK$
for any
![]() $w\in \Lambda _m$
(clearly, this k can be chosen to work for all m), we then have
$w\in \Lambda _m$
(clearly, this k can be chosen to work for all m), we then have
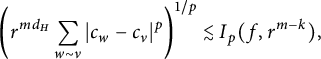 $$\begin{align*}\left(r^{md_H}\sum_{w\sim \nu}|c_w-c_\nu|^p\right)^{1/p}\lesssim I_p(f,r^{m-k}),\end{align*}$$
$$\begin{align*}\left(r^{md_H}\sum_{w\sim \nu}|c_w-c_\nu|^p\right)^{1/p}\lesssim I_p(f,r^{m-k}),\end{align*}$$
thus, we get the first desired estimate. The estimate for
![]() $\|\Delta u_m\|_{L^p(K)}$
is essentially the same.
$\|\Delta u_m\|_{L^p(K)}$
is essentially the same.
Now, we prove the main result of this section.
Proposition 5.3 For
![]() $1<p<\infty $
,
$1<p<\infty $
,
![]() $1\leq q\leq \infty $
and
$1\leq q\leq \infty $
and
![]() $0<\sigma <2$
, we have
$0<\sigma <2$
, we have
![]() $\Lambda ^{p,q}_\sigma (K)\subset B^{p,q}_\sigma (K)$
with
$\Lambda ^{p,q}_\sigma (K)\subset B^{p,q}_\sigma (K)$
with
![]() $\|\cdot \|_{B^{p,q}_\sigma (K)}\lesssim \|\cdot \|_{\Lambda ^{p,q}_\sigma (K)}$
.
$\|\cdot \|_{B^{p,q}_\sigma (K)}\lesssim \|\cdot \|_{\Lambda ^{p,q}_\sigma (K)}$
.
Proof Let
![]() $f\in \Lambda ^{p,q}_\sigma (K)$
. We define a sequence of functions
$f\in \Lambda ^{p,q}_\sigma (K)$
. We define a sequence of functions
![]() $u_m$
in
$u_m$
in
![]() $H^p_2(K)$
by Lemma 5.2, and we take
$H^p_2(K)$
by Lemma 5.2, and we take
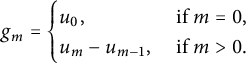 $$\begin{align*}g_m=\begin{cases} u_0,&\text{ if }m=0,\\ u_m-u_{m-1},&\text{ if }m>0. \end{cases}\end{align*}$$
$$\begin{align*}g_m=\begin{cases} u_0,&\text{ if }m=0,\\ u_m-u_{m-1},&\text{ if }m>0. \end{cases}\end{align*}$$
For
![]() $m\geq 0$
, by Lemma 5.2, we have the estimate
$m\geq 0$
, by Lemma 5.2, we have the estimate
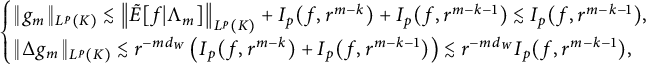 $$\begin{align*}\begin{cases} \|g_m\|_{L^p(K)}\lesssim \left\|\tilde{E}[f|\Lambda_m]\right\|_{L^p(K)}+I_p(f,r^{m-k})+I_p(f,r^{m-k-1})\lesssim I_p(f,r^{m-k-1}),\\ \|\Delta g_m\|_{L^p(K)}\lesssim r^{-md_W} \left(I_p(f,r^{m-k})+I_p(f,r^{m-k-1})\right)\lesssim r^{-md_W}I_p(f,r^{m-k-1}), \end{cases}\end{align*}$$
$$\begin{align*}\begin{cases} \|g_m\|_{L^p(K)}\lesssim \left\|\tilde{E}[f|\Lambda_m]\right\|_{L^p(K)}+I_p(f,r^{m-k})+I_p(f,r^{m-k-1})\lesssim I_p(f,r^{m-k-1}),\\ \|\Delta g_m\|_{L^p(K)}\lesssim r^{-md_W} \left(I_p(f,r^{m-k})+I_p(f,r^{m-k-1})\right)\lesssim r^{-md_W}I_p(f,r^{m-k-1}), \end{cases}\end{align*}$$
where k is the same as Lemma 5.2, and we use Lemma 4.3(a) in the second estimate of the first formula. Taking
![]() $\lambda =r^{d_W}$
,
$\lambda =r^{d_W}$
,
![]() $X_0=L^p(K)$
and
$X_0=L^p(K)$
and
![]() $X_1=H^p_2(K)$
in Lemma 5.1, it then follows that
$X_1=H^p_2(K)$
in Lemma 5.1, it then follows that
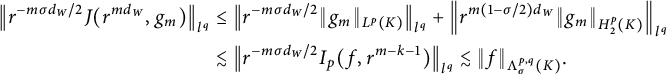 $$\begin{align*}\begin{aligned} \left\|r^{-m\sigma d_W/2}J(r^{md_W},g_m)\right\|_{l^q}&\leq \left\|r^{-m\sigma d_W/2}\|g_m\|_{L^p(K)}\right\|_{l^q}+\left\|r^{m(1-\sigma/2)d_W}\|g_m\|_{H^p_2(K)}\right\|_{l^q}\\ &\lesssim \left\|r^{-m\sigma d_W/2}I_p(f,r^{m-k-1})\right\|_{l^q}\lesssim\|f\|_{\Lambda^{p,q}_\sigma(K)}. \end{aligned}\end{align*}$$
$$\begin{align*}\begin{aligned} \left\|r^{-m\sigma d_W/2}J(r^{md_W},g_m)\right\|_{l^q}&\leq \left\|r^{-m\sigma d_W/2}\|g_m\|_{L^p(K)}\right\|_{l^q}+\left\|r^{m(1-\sigma/2)d_W}\|g_m\|_{H^p_2(K)}\right\|_{l^q}\\ &\lesssim \left\|r^{-m\sigma d_W/2}I_p(f,r^{m-k-1})\right\|_{l^q}\lesssim\|f\|_{\Lambda^{p,q}_\sigma(K)}. \end{aligned}\end{align*}$$
It is easy to see that
![]() $f=\sum _{m=0}^\infty g_m$
, so combining with Lemma 2.6, we have
$f=\sum _{m=0}^\infty g_m$
, so combining with Lemma 2.6, we have
![]() $f\in B^{p,q}_\sigma (K)$
with
$f\in B^{p,q}_\sigma (K)$
with
![]() $\|f\|_{B^{p,q}_\sigma (K)}\lesssim \|f\|_{\Lambda ^{p,q}_{\sigma }(K)}$
.
$\|f\|_{B^{p,q}_\sigma (K)}\lesssim \|f\|_{\Lambda ^{p,q}_{\sigma }(K)}$
.
Before ending this section, we mention that the same method can be applied to show that
![]() $\Lambda ^{p,q}_{\sigma ,(1)}(K)\subset B^{p,q}_\sigma (K)$
for
$\Lambda ^{p,q}_{\sigma ,(1)}(K)\subset B^{p,q}_\sigma (K)$
for
![]() $\mathscr {L}_1(p)<\sigma <2$
. In this case, for each
$\mathscr {L}_1(p)<\sigma <2$
. In this case, for each
![]() $m\geq 0$
, we choose a piecewise harmonic function of level m that coincides with f at
$m\geq 0$
, we choose a piecewise harmonic function of level m that coincides with f at
![]() $V_{\Lambda _m}$
, then modify it in a neighborhood of
$V_{\Lambda _m}$
, then modify it in a neighborhood of
![]() $V_{\Lambda _m}$
to get a function
$V_{\Lambda _m}$
to get a function
![]() $u_m$
in
$u_m$
in
![]() $H^p_2(K)$
analogous to that in Lemma 5.2. Since the idea is essentially the same, we omit the proof, and state the result as follows.
$H^p_2(K)$
analogous to that in Lemma 5.2. Since the idea is essentially the same, we omit the proof, and state the result as follows.
Proposition 5.4 For
![]() $1<p<\infty $
,
$1<p<\infty $
,
![]() $1\leq q\leq \infty $
and
$1\leq q\leq \infty $
and
![]() $\mathscr {L}_1(p)<\sigma <2$
, we have
$\mathscr {L}_1(p)<\sigma <2$
, we have
![]() $\Lambda ^{p,q}_{\sigma ,(1)}(K)\subset B^{p,q}_\sigma (K)$
with
$\Lambda ^{p,q}_{\sigma ,(1)}(K)\subset B^{p,q}_\sigma (K)$
with
![]() $\|\cdot \|_{B^{p,q}_\sigma (K)}\lesssim \|\cdot \|_{\Lambda ^{p,q}_{\sigma ,(1)}(K)}$
.
$\|\cdot \|_{B^{p,q}_\sigma (K)}\lesssim \|\cdot \|_{\Lambda ^{p,q}_{\sigma ,(1)}(K)}$
.
6 Embedding
 $B^{p,q}_\sigma (K)$
into
$B^{p,q}_\sigma (K)$
into
 $\Lambda ^{p,q}_\sigma (K)$
$\Lambda ^{p,q}_\sigma (K)$
We will prove
![]() $B^{p,q}_\sigma (K)\subset \Lambda ^{p,q}_\sigma (K)$
for
$B^{p,q}_\sigma (K)\subset \Lambda ^{p,q}_\sigma (K)$
for
![]() $0<\sigma <\mathscr C(p)$
in this section. Also, we will show that
$0<\sigma <\mathscr C(p)$
in this section. Also, we will show that
![]() $B^{p,q}_\sigma (K)\subset \Lambda ^{p,q}_{\sigma ,(1)}(K)$
for
$B^{p,q}_\sigma (K)\subset \Lambda ^{p,q}_{\sigma ,(1)}(K)$
for
![]() $\mathscr {L}_1(p)<\sigma <2$
.
$\mathscr {L}_1(p)<\sigma <2$
.
First, let’s look at two easy lemmas.
Lemma 6.1 Let
![]() $\left \{X_m,\|\cdot \|_{X_m}\right \}_{m\geq 0}$
be a sequence of Banach spaces. For
$\left \{X_m,\|\cdot \|_{X_m}\right \}_{m\geq 0}$
be a sequence of Banach spaces. For
![]() $1\leq q\leq \infty $
and
$1\leq q\leq \infty $
and
![]() $\alpha>0$
, let
$\alpha>0$
, let
be the space with norm
![]() $\|\boldsymbol {s}\|_{l^q_\alpha (X_\cdot )}=\big \|\alpha ^{-m}\|s_m\|_{X_m}\big \|_{l^q}$
. Then, for
$\|\boldsymbol {s}\|_{l^q_\alpha (X_\cdot )}=\big \|\alpha ^{-m}\|s_m\|_{X_m}\big \|_{l^q}$
. Then, for
![]() $\alpha _0\neq \alpha _1$
,
$\alpha _0\neq \alpha _1$
,
![]() $0<\theta <1$
and
$0<\theta <1$
and
![]() $1\leq q_0,q_1,q\leq \infty $
, we have
$1\leq q_0,q_1,q\leq \infty $
, we have
This lemma is revised from Theorem 5.6.1 in book [Reference Bergh and Löfström9] with a same argument. The difference is that we allow each coordinate taking values in different spaces, which does not bring any difficult to the proof. As an immediate consequence, we can see the following interpolation lemma for
![]() $\Lambda ^{p,q}_\sigma (K)$
and
$\Lambda ^{p,q}_\sigma (K)$
and
![]() $\Lambda ^{p,q}_{\sigma ,(1)}(K)$
.
$\Lambda ^{p,q}_{\sigma ,(1)}(K)$
.
Lemma 6.2 Let
![]() $1\leq p,q,q_0,q_1\leq \infty $
,
$1\leq p,q,q_0,q_1\leq \infty $
,
![]() $0<\sigma _0,\sigma _1<\infty $
and
$0<\sigma _0,\sigma _1<\infty $
and
![]() $0<\theta <1$
. We have:
$0<\theta <1$
. We have:
(a).
![]() $\left (\Lambda ^{p,q_0}_{\sigma _0}(K),\Lambda ^{p,q_1}_{\sigma _1}(K)\right )_{\theta ,q}\subset \Lambda ^{p,q}_{\sigma _\theta }(K)$
;
$\left (\Lambda ^{p,q_0}_{\sigma _0}(K),\Lambda ^{p,q_1}_{\sigma _1}(K)\right )_{\theta ,q}\subset \Lambda ^{p,q}_{\sigma _\theta }(K)$
;
(b).
![]() $\left (\Lambda ^{p,q_0}_{\sigma _0,(1)}(K),\Lambda ^{p,q_1}_{\sigma _1,(1)}(K)\right )_{\theta ,q}\subset \Lambda ^{p,q}_{\sigma _\theta ,(1)}(K)$
,
$\left (\Lambda ^{p,q_0}_{\sigma _0,(1)}(K),\Lambda ^{p,q_1}_{\sigma _1,(1)}(K)\right )_{\theta ,q}\subset \Lambda ^{p,q}_{\sigma _\theta ,(1)}(K)$
,
with
![]() $\sigma _\theta =(1-\theta )\sigma _0+\theta \sigma _1$
.
$\sigma _\theta =(1-\theta )\sigma _0+\theta \sigma _1$
.
From now on, we will separate our consideration into two cases, according to
![]() $(\frac {1}{p},\sigma )$
belongs to
$(\frac {1}{p},\sigma )$
belongs to
![]() $\mathscr A_1$
or
$\mathscr A_1$
or
![]() $\mathscr A_2$
. We will deal with the border between
$\mathscr A_2$
. We will deal with the border between
![]() $\mathscr {A}_1$
and
$\mathscr {A}_1$
and
![]() $\mathscr {A}_2$
by using Lemma 6.2. For the region
$\mathscr {A}_2$
by using Lemma 6.2. For the region
![]() $\mathscr A_1$
, in fact, we mainly consider a larger region
$\mathscr A_1$
, in fact, we mainly consider a larger region
![]() $\mathscr B:=\left \{(\frac 1 p,\sigma ): \mathscr L_1(p)<\sigma <\mathscr L_2(p)\right \}$
instead.
$\mathscr B:=\left \{(\frac 1 p,\sigma ): \mathscr L_1(p)<\sigma <\mathscr L_2(p)\right \}$
instead.
6.1 On regions
 $\mathscr {A}_1$
and
$\mathscr {A}_1$
and
 $\mathscr B$
$\mathscr B$
To reach the goal that
![]() $B^{p,q}_\sigma (K)\subset \Lambda ^{p,q}_\sigma (K)$
for
$B^{p,q}_\sigma (K)\subset \Lambda ^{p,q}_\sigma (K)$
for
![]() $(\frac 1 p,\sigma )\in \mathscr A_1$
, by Theorem 4.8(c), it suffices to prove
$(\frac 1 p,\sigma )\in \mathscr A_1$
, by Theorem 4.8(c), it suffices to prove
![]() $B^{p,q}_\sigma (K)\subset \Lambda ^{p,q}_{\sigma ,(1)}(K)$
. We will fulfill this for the parameter region
$B^{p,q}_\sigma (K)\subset \Lambda ^{p,q}_{\sigma ,(1)}(K)$
. We will fulfill this for the parameter region
![]() $\mathscr B=\left \{(\frac 1 p,\sigma ): \mathscr L_1(p)<\sigma <\mathscr L_2(p)\right \}$
, which is the region between the two critical lines
$\mathscr B=\left \{(\frac 1 p,\sigma ): \mathscr L_1(p)<\sigma <\mathscr L_2(p)\right \}$
, which is the region between the two critical lines
![]() $\mathscr L_1$
and
$\mathscr L_1$
and
![]() $\mathscr L_2$
, and of cause contains
$\mathscr L_2$
, and of cause contains
![]() $\mathscr A_1$
.
$\mathscr A_1$
.
Note that we can write each
![]() $f\in C(K)$
as a unique series,
$f\in C(K)$
as a unique series,
and in addition, by Theorem 4.8(b), it always holds
Let’s start with some observations.
Lemma 6.3 Let
![]() $1<p,q<\infty $
and
$1<p,q<\infty $
and
![]() $0<\sigma <2$
. Write
$0<\sigma <2$
. Write
![]() $p'=\frac {p}{p-1}$
and
$p'=\frac {p}{p-1}$
and
![]() $q'=\frac {q}{q-1}$
. Then there is a continuous sesquilinear form
$q'=\frac {q}{q-1}$
. Then there is a continuous sesquilinear form
![]() $\tilde {\mathcal {E}}(\cdot ,\cdot )$
on
$\tilde {\mathcal {E}}(\cdot ,\cdot )$
on
![]() $B^{p,q}_{\sigma }(K)\times B^{p',q'}_{2-\sigma }(K)$
such that
$B^{p,q}_{\sigma }(K)\times B^{p',q'}_{2-\sigma }(K)$
such that
Proof First, by the definition of
![]() $\Delta _N$
, we can see that
$\Delta _N$
, we can see that
for any
![]() $f\in L^p(K)\cap dom\mathcal {E}$
and
$f\in L^p(K)\cap dom\mathcal {E}$
and
![]() $g\in H^{p'}_{2}(K)$
. So there is a continuous sesquilinear form
$g\in H^{p'}_{2}(K)$
. So there is a continuous sesquilinear form
![]() $\tilde {\mathcal {E}}:L^p(K)\times H^{p'}_{2}(K)\to \mathbb {C}$
, such that
$\tilde {\mathcal {E}}:L^p(K)\times H^{p'}_{2}(K)\to \mathbb {C}$
, such that
![]() $\tilde {\mathcal {E}}(f,g)=\mathcal {E}(f,g)$
for any
$\tilde {\mathcal {E}}(f,g)=\mathcal {E}(f,g)$
for any
![]() $f\in L^p(K)\cap dom\mathcal {E}$
and
$f\in L^p(K)\cap dom\mathcal {E}$
and
![]() $g\in H^{p'}_2(K)$
. In addition, we can see that
$g\in H^{p'}_2(K)$
. In addition, we can see that
![]() $|\mathcal {E}(f,g)|\leq \|f\|_{H^p_2(K)}\cdot \|g\|_{L^{p'}(K)}$
for any
$|\mathcal {E}(f,g)|\leq \|f\|_{H^p_2(K)}\cdot \|g\|_{L^{p'}(K)}$
for any
![]() $f\in H^p_2(K)$
and
$f\in H^p_2(K)$
and
![]() $g\in H_2^{p'}(K)$
.
$g\in H_2^{p'}(K)$
.
As a consequence, the mapping
![]() $f\to \tilde {\mathcal {E}}(f,\cdot )$
is continuous from
$f\to \tilde {\mathcal {E}}(f,\cdot )$
is continuous from
![]() $L^p(K)$
to
$L^p(K)$
to
![]() $\left (H^{p'}_{2}(K)\right )^*$
, and is continuous from
$\left (H^{p'}_{2}(K)\right )^*$
, and is continuous from
![]() $H^p_{2}(K)$
to
$H^p_{2}(K)$
to
![]() $\left (L^{p'}(K)\right )^*$
since
$\left (L^{p'}(K)\right )^*$
since
![]() $H^{p'}_{2}(K)$
is dense in
$H^{p'}_{2}(K)$
is dense in
![]() $L^{p'}(K)$
, where we use
$L^{p'}(K)$
, where we use
![]() $*$
to denote the dual space. Using the theorem of real interpolation (see [Reference Bergh and Löfström9, Theorem 3.7.1] Theorem 3.7.1), we have
$*$
to denote the dual space. Using the theorem of real interpolation (see [Reference Bergh and Löfström9, Theorem 3.7.1] Theorem 3.7.1), we have
![]() $f\to \tilde {\mathcal {E}}(f,\cdot )$
is continuous from
$f\to \tilde {\mathcal {E}}(f,\cdot )$
is continuous from
![]() $B^{p,q}_{\sigma }(K)$
to
$B^{p,q}_{\sigma }(K)$
to
![]() $\left (B^{p',q'}_{2-\sigma }(K)\right )^*$
. So
$\left (B^{p',q'}_{2-\sigma }(K)\right )^*$
. So
![]() $\tilde {\mathcal {E}}$
extends to a continuous sesquilinear form on
$\tilde {\mathcal {E}}$
extends to a continuous sesquilinear form on
![]() $B^{p,q}_{\sigma }(K)\times B^{p',q'}_{2-\sigma }(K)$
.
$B^{p,q}_{\sigma }(K)\times B^{p',q'}_{2-\sigma }(K)$
.
Lemma 6.4 For
![]() $1\leq p,q\leq \infty $
, we have
$1\leq p,q\leq \infty $
, we have
![]() $H^p_2(K)\subset \Lambda ^{p,\infty }_{2,(1)}(K)$
. In addition, this implies
$H^p_2(K)\subset \Lambda ^{p,\infty }_{2,(1)}(K)$
. In addition, this implies
![]() $H^p_2(K)\subset \Lambda ^{p,q}_{\sigma ,(1)}(K)$
for each
$H^p_2(K)\subset \Lambda ^{p,q}_{\sigma ,(1)}(K)$
for each
![]() $0<\sigma <2$
.
$0<\sigma <2$
.
Proof In fact, for each
![]() $f\in H^p_2(K)$
and
$f\in H^p_2(K)$
and
![]() $x\in V_{\Lambda _m}$
, we have
$x\in V_{\Lambda _m}$
, we have
where
![]() $U_{x,m}$
is the same we defined in the proof of Lemma 5.2, and
$U_{x,m}$
is the same we defined in the proof of Lemma 5.2, and
![]() $\psi _{x,m}$
is a piecewise harmonic function supported on
$\psi _{x,m}$
is a piecewise harmonic function supported on
![]() $U_{x,m}$
, with
$U_{x,m}$
, with
![]() $\psi _{x,m}(x)=1$
and
$\psi _{x,m}(x)=1$
and
![]() $\psi _{x,m}|_{V_{\Lambda _m}\setminus \{x\}}\equiv 0$
, and is harmonic in each
$\psi _{x,m}|_{V_{\Lambda _m}\setminus \{x\}}\equiv 0$
, and is harmonic in each
![]() $F_wK,w\in \Lambda _m$
. As a consequence, we get
$F_wK,w\in \Lambda _m$
. As a consequence, we get
which yields that
![]() $H^p_2(K)\subset \Lambda ^{p,\infty }_{2,(1)}(K)$
, noticing that
$H^p_2(K)\subset \Lambda ^{p,\infty }_{2,(1)}(K)$
, noticing that
![]() $-2d_W/2+1+d_H/p=-d_H/p'$
since
$-2d_W/2+1+d_H/p=-d_H/p'$
since
![]() $d_W=1+d_H$
. Finally,
$d_W=1+d_H$
. Finally,
![]() $H^p_2(K)\subset \Lambda ^{p,\infty }_{2,(1)}(K)\subset \Lambda ^{p,q}_{\sigma ,(1)}(K)$
since
$H^p_2(K)\subset \Lambda ^{p,\infty }_{2,(1)}(K)\subset \Lambda ^{p,q}_{\sigma ,(1)}(K)$
since
![]() $r^{m(-\sigma d_W/2+1+d_H/p)}\|H_{\Lambda _m}f\|_{l^p(V_{\Lambda _m})}\leq r^{m(2-\sigma )d_W/2}\|f\|_{\Lambda ^{p,\infty }_{2,(1)}(K)}$
.
$r^{m(-\sigma d_W/2+1+d_H/p)}\|H_{\Lambda _m}f\|_{l^p(V_{\Lambda _m})}\leq r^{m(2-\sigma )d_W/2}\|f\|_{\Lambda ^{p,\infty }_{2,(1)}(K)}$
.
Proposition 6.5 For
![]() $1<p<\infty $
,
$1<p<\infty $
,
![]() $1\leq q\leq \infty $
and
$1\leq q\leq \infty $
and
![]() $\mathscr {L}_1(p)<\sigma <\mathscr {L}_2(p)$
, we have
$\mathscr {L}_1(p)<\sigma <\mathscr {L}_2(p)$
, we have
![]() $B^{p,q}_\sigma (K)=\Lambda ^{p,q}_{\sigma ,(1)}(K)$
with
$B^{p,q}_\sigma (K)=\Lambda ^{p,q}_{\sigma ,(1)}(K)$
with
![]() $\|\cdot \|_{\Lambda ^{p,q}_{\sigma ,(1)}(K)}\asymp \|\cdot \|_{B^{p,q}_\sigma (K)}$
. In particular, if
$\|\cdot \|_{\Lambda ^{p,q}_{\sigma ,(1)}(K)}\asymp \|\cdot \|_{B^{p,q}_\sigma (K)}$
. In particular, if
![]() $(\frac 1p,\sigma )\in \mathscr A_1$
, we have
$(\frac 1p,\sigma )\in \mathscr A_1$
, we have
![]() $B^{p,q}_\sigma (K)=\Lambda ^{p,q}_\sigma (K)$
with
$B^{p,q}_\sigma (K)=\Lambda ^{p,q}_\sigma (K)$
with
![]() $\|\cdot \|_{\Lambda ^{p,q}_\sigma (K)}\asymp \|\cdot \|_{B^{p,q}_\sigma (K)}.$
$\|\cdot \|_{\Lambda ^{p,q}_\sigma (K)}\asymp \|\cdot \|_{B^{p,q}_\sigma (K)}.$
Proof By Theorem 4.8(c), it suffices to prove the first result. Also, by Lemma 6.2(b) and Proposition 5.4, it suffices to consider the
![]() $1<q<\infty $
case.
$1<q<\infty $
case.
By Lemma 6.3, there exists
![]() $\tilde {\mathcal {E}}$
on
$\tilde {\mathcal {E}}$
on
![]() $B^{p,q}_\sigma (K)\times B^{p',q'}_{2-\sigma }(K)$
with
$B^{p,q}_\sigma (K)\times B^{p',q'}_{2-\sigma }(K)$
with
![]() $p'=\frac {p}{p-1},q'=\frac {q}{q-1}$
satisfying (6.1). In the following claims, we provide an exact formula of
$p'=\frac {p}{p-1},q'=\frac {q}{q-1}$
satisfying (6.1). In the following claims, we provide an exact formula of
![]() $\tilde {\mathcal {E}}$
on
$\tilde {\mathcal {E}}$
on
![]() $\Lambda ^{p,q}_{\sigma ,(1)}(K)\times \Lambda ^{p',q'}_{2-\sigma ,(1)}(K)$
.
$\Lambda ^{p,q}_{\sigma ,(1)}(K)\times \Lambda ^{p',q'}_{2-\sigma ,(1)}(K)$
.
Claim 1 Let
![]() $M\geq 0$
,
$M\geq 0$
,
![]() $f=\sum _{m=0}^M f_m$
and
$f=\sum _{m=0}^M f_m$
and
![]() $g=\sum _{m=0}^M g_m$
with
$g=\sum _{m=0}^M g_m$
with
![]() $f_m,g_m\in J_m$
,
$f_m,g_m\in J_m$
,
![]() $0\leq m\leq M$
. We have
$0\leq m\leq M$
. We have
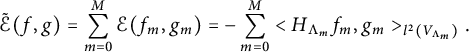 $$\begin{align*}\tilde{\mathcal{E}}(f,g)=\sum_{m=0}^M \mathcal{E}(f_m,g_m)=-\sum_{m=0}^M <H_{\Lambda_m}f_m,g_m>_{l^2(V_{\Lambda_m})}.\\[-42pt]\end{align*}$$
$$\begin{align*}\tilde{\mathcal{E}}(f,g)=\sum_{m=0}^M \mathcal{E}(f_m,g_m)=-\sum_{m=0}^M <H_{\Lambda_m}f_m,g_m>_{l^2(V_{\Lambda_m})}.\\[-42pt]\end{align*}$$
Proof Clearly, we have
![]() $f\in dom\mathcal {E}\cap B^{p,q}_\sigma (K)$
, and
$f\in dom\mathcal {E}\cap B^{p,q}_\sigma (K)$
, and
![]() $g\in B^{p',q'}_{2-\sigma }(K)$
by Proposition 5.4, thus, there is a sequence of functions
$g\in B^{p',q'}_{2-\sigma }(K)$
by Proposition 5.4, thus, there is a sequence of functions
![]() $g^{(n)}$
in
$g^{(n)}$
in
![]() $ H^{p'}_2(K)$
converging to g in
$ H^{p'}_2(K)$
converging to g in
![]() $B^{p',q'}_{2-\sigma }(K)$
. For each n, by Lemma 6.3, we have
$B^{p',q'}_{2-\sigma }(K)$
. For each n, by Lemma 6.3, we have
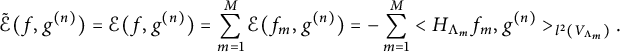 $$\begin{align*}\tilde{\mathcal{E}}(f,g^{(n)})=\mathcal{E}(f,g^{(n)})=\sum_{m=1}^M\mathcal{E}(f_m,g^{(n)})=-\sum_{m=1}^M<H_{\Lambda_m}f_m,g^{(n)}>_{l^2(V_{\Lambda_m})}.\end{align*}$$
$$\begin{align*}\tilde{\mathcal{E}}(f,g^{(n)})=\mathcal{E}(f,g^{(n)})=\sum_{m=1}^M\mathcal{E}(f_m,g^{(n)})=-\sum_{m=1}^M<H_{\Lambda_m}f_m,g^{(n)}>_{l^2(V_{\Lambda_m})}.\end{align*}$$
Letting
![]() $n\rightarrow \infty $
, we have the claim proved, since
$n\rightarrow \infty $
, we have the claim proved, since
![]() $g^{(n)}$
converges to g in
$g^{(n)}$
converges to g in
![]() $B^{p',q'}_{2-\sigma }(K)$
and thus converges uniformly as
$B^{p',q'}_{2-\sigma }(K)$
and thus converges uniformly as
![]() $2-\sigma>\mathscr {L}_1(p')$
.
$2-\sigma>\mathscr {L}_1(p')$
.
Claim 2 Let
![]() $f=\sum _{m=0}^\infty f_m$
and
$f=\sum _{m=0}^\infty f_m$
and
![]() $g=\sum _{m=0}^\infty g_m$
with
$g=\sum _{m=0}^\infty g_m$
with
![]() $f_m,g_m\in J_m,\forall m\geq 0$
, and
$f_m,g_m\in J_m,\forall m\geq 0$
, and
We have
Proof By using Claim 1, we have
![]() $\tilde {\mathcal {E}}\left (\sum _{m=0}^Mf_m,\sum _{m=0}^Mg_m\right )=-\sum _{m=0}^M<H_{\Lambda _m}f_m,g_m>_{l^2(V_{\Lambda _m})}$
for any
$\tilde {\mathcal {E}}\left (\sum _{m=0}^Mf_m,\sum _{m=0}^Mg_m\right )=-\sum _{m=0}^M<H_{\Lambda _m}f_m,g_m>_{l^2(V_{\Lambda _m})}$
for any
![]() $M\geq 0$
. Letting
$M\geq 0$
. Letting
![]() $M\rightarrow \infty $
, then the claim follows, since the left side converges to
$M\rightarrow \infty $
, then the claim follows, since the left side converges to
![]() $\tilde {\mathcal {E}}(f,g)$
as
$\tilde {\mathcal {E}}(f,g)$
as
![]() $\sum _{m=0}^M f_m$
converges to f in
$\sum _{m=0}^M f_m$
converges to f in
![]() $B^{p,q}_\sigma (K)$
and
$B^{p,q}_\sigma (K)$
and
![]() $\sum _{m=0}^M g_m$
converges to g in
$\sum _{m=0}^M g_m$
converges to g in
![]() $B^{p',q'}_{2-\sigma }(K)$
by Proposition 5.4.
$B^{p',q'}_{2-\sigma }(K)$
by Proposition 5.4.
Claim 3 Let
![]() $f=\sum _{m=0}^\infty f_m$
with
$f=\sum _{m=0}^\infty f_m$
with
![]() $f_m\in J_m,\forall m\geq 0$
, and
$f_m\in J_m,\forall m\geq 0$
, and
![]() $\big \|r^{-m\sigma d_W/2}\|f_m\|_{L^p(K)}\big \|_{l^q}<\infty $
. We have
$\big \|r^{-m\sigma d_W/2}\|f_m\|_{L^p(K)}\big \|_{l^q}<\infty $
. We have
![]() $\big \|r^{-m\sigma d_W/2}\|f_m\|_{L^p(K)}\big \|_{l^q}\lesssim \|f\|_{B^{p,q}_\sigma (K)}$
.
$\big \|r^{-m\sigma d_W/2}\|f_m\|_{L^p(K)}\big \|_{l^q}\lesssim \|f\|_{B^{p,q}_\sigma (K)}$
.
Proof The space
![]() $l^{q'}\left (l^{p'}(V_{\Lambda _\cdot })\right )$
can be identified with the dual space of
$l^{q'}\left (l^{p'}(V_{\Lambda _\cdot })\right )$
can be identified with the dual space of
![]() $l^{q}\left (l^{p}(V_{\Lambda _\cdot })\right )$
in a natural way, and thus, we can find
$l^{q}\left (l^{p}(V_{\Lambda _\cdot })\right )$
in a natural way, and thus, we can find
![]() $g=\sum _{m=0}^\infty g_m$
, with
$g=\sum _{m=0}^\infty g_m$
, with
![]() $g_m\in J_m$
and
$g_m\in J_m$
and
![]() $0<\big \|r^{m(\sigma -2)d_W/2}\|g_m\|_{L^{p'}(K)}\big \|_{l^{q'}}<\infty $
, such that
$0<\big \|r^{m(\sigma -2)d_W/2}\|g_m\|_{L^{p'}(K)}\big \|_{l^{q'}}<\infty $
, such that
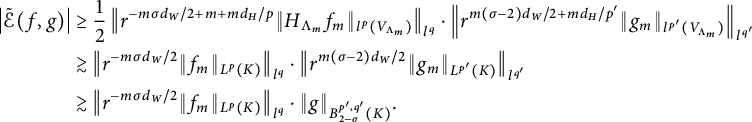 $$\begin{align*}\begin{aligned} \big|\tilde{\mathcal{E}}(f,g)\big|&\geq \frac{1}{2}\left\|r^{-m\sigma d_W/2+m+md_H/p}\|H_{\Lambda_m}f_m\|_{l^p({V}_{\Lambda_m})}\right\|_{l^q}\cdot\left\|r^{m(\sigma-2)d_W/2+md_H/{p'}}\|g_m\|_{l^{p'}({V}_{\Lambda_m})}\right\|_{l^{q'}}\\ &\gtrsim\left\|r^{-m\sigma d_W/2}\|f_m\|_{L^p(K)}\right\|_{l^q}\cdot \left\|r^{m(\sigma -2)d_W/2}\|g_m\|_{L^{p'}(K)}\right\|_{l^{q'}}\\ &\gtrsim\left\|r^{-m\sigma d_W/2}\|f_m\|_{L^p(K)}\right\|_{l^q}\cdot \|g\|_{B^{p',q'}_{2-\sigma}(K)}. \end{aligned}\end{align*}$$
$$\begin{align*}\begin{aligned} \big|\tilde{\mathcal{E}}(f,g)\big|&\geq \frac{1}{2}\left\|r^{-m\sigma d_W/2+m+md_H/p}\|H_{\Lambda_m}f_m\|_{l^p({V}_{\Lambda_m})}\right\|_{l^q}\cdot\left\|r^{m(\sigma-2)d_W/2+md_H/{p'}}\|g_m\|_{l^{p'}({V}_{\Lambda_m})}\right\|_{l^{q'}}\\ &\gtrsim\left\|r^{-m\sigma d_W/2}\|f_m\|_{L^p(K)}\right\|_{l^q}\cdot \left\|r^{m(\sigma -2)d_W/2}\|g_m\|_{L^{p'}(K)}\right\|_{l^{q'}}\\ &\gtrsim\left\|r^{-m\sigma d_W/2}\|f_m\|_{L^p(K)}\right\|_{l^q}\cdot \|g\|_{B^{p',q'}_{2-\sigma}(K)}. \end{aligned}\end{align*}$$
On the other hand, we have
![]() $\big |\tilde {\mathcal {E}}(f,g)\big |\lesssim \|f\|_{B^{p,q}_\sigma (K)}\cdot \|g\|_{B^{p',q'}_{2-\sigma }(K)}$
. The estimate follows.
$\big |\tilde {\mathcal {E}}(f,g)\big |\lesssim \|f\|_{B^{p,q}_\sigma (K)}\cdot \|g\|_{B^{p',q'}_{2-\sigma }(K)}$
. The estimate follows.
Now, combining Claim 3 and Proposition 5.4, we can see that
![]() $\Lambda ^{p,q}_{\sigma ,(1)}(K)$
is a closed subset of
$\Lambda ^{p,q}_{\sigma ,(1)}(K)$
is a closed subset of
![]() $B^{p,q}_\sigma (K)$
. On the other hand, we have
$B^{p,q}_\sigma (K)$
. On the other hand, we have
![]() $H^p_2(K)\subset \Lambda ^{p,q}_{\sigma ,(1)}(K)$
by Lemma 6.4. So the desired result follows since
$H^p_2(K)\subset \Lambda ^{p,q}_{\sigma ,(1)}(K)$
by Lemma 6.4. So the desired result follows since
![]() $H^p_2(K)$
is dense in
$H^p_2(K)$
is dense in
![]() $B^{p,q}_\sigma (K)$
.
$B^{p,q}_\sigma (K)$
.
Finally, for
![]() $1<p<\infty $
,
$1<p<\infty $
,
![]() $q=1,\infty $
and
$q=1,\infty $
and
![]() $\mathscr {L}_1(p)<\sigma <\mathscr {L}_2(p)$
, we pick
$\mathscr {L}_1(p)<\sigma <\mathscr {L}_2(p)$
, we pick
![]() $\mathscr {L}_1(p)<\sigma _1<\sigma <\sigma _2<\mathscr {L}_2(p)$
and
$\mathscr {L}_1(p)<\sigma _1<\sigma <\sigma _2<\mathscr {L}_2(p)$
and
![]() $\theta \in (0,1)$
such that
$\theta \in (0,1)$
such that
![]() $\sigma =(1-\theta )\sigma _1+\theta \sigma _2$
, then
$\sigma =(1-\theta )\sigma _1+\theta \sigma _2$
, then
by Lemma 6.2(b), Lemma 2.6, and the reiteration theorem of real interpolation. Hence,
![]() $\Lambda ^{p,q}_\sigma (K)=B^{p,q}_\sigma (K)$
by Proposition 5.4.
$\Lambda ^{p,q}_\sigma (K)=B^{p,q}_\sigma (K)$
by Proposition 5.4.
By applying Propositions 5.4 and 6.5 and Lemma 6.2(b), we can finish the proof of Theorem 4.9.
Proof of Theorem 4.9
Let’s fix
![]() $1<p<\infty $
,
$1<p<\infty $
,
![]() $1\leq q\leq \infty $
and
$1\leq q\leq \infty $
and
![]() $\mathscr {L}_1(p)<\sigma <2$
, and we choose
$\mathscr {L}_1(p)<\sigma <2$
, and we choose
![]() $\mathscr {L}_1(p)<\sigma _1<\sigma \wedge \mathscr {L}_2(p)$
and
$\mathscr {L}_1(p)<\sigma _1<\sigma \wedge \mathscr {L}_2(p)$
and
![]() $\theta \in (0,1)$
such that
$\theta \in (0,1)$
such that
![]() $\sigma =(1-\theta )\sigma _1+2\theta $
. Then, by Proposition 6.5, we know that
$\sigma =(1-\theta )\sigma _1+2\theta $
. Then, by Proposition 6.5, we know that
![]() $B^{p,q}_{\sigma _1}(K)=\Lambda ^{p,q}_{\sigma _1,(1)}(K)$
; by Lemma 6.4, we know that
$B^{p,q}_{\sigma _1}(K)=\Lambda ^{p,q}_{\sigma _1,(1)}(K)$
; by Lemma 6.4, we know that
![]() $H^p_2(K)\subset \Lambda ^{p,\infty }_{2,(1)}(K)$
. Hence,
$H^p_2(K)\subset \Lambda ^{p,\infty }_{2,(1)}(K)$
. Hence,
by Lemma 2.6, the reiteration theorem of real interpolation and Lemma 6.2(b). Combining this with Proposition 5.4, the theorem follows.
6.2 On region
 $\mathscr {A}_2$
$\mathscr {A}_2$
It remains to show
![]() $B^{p,q}_\sigma (K)\subset \Lambda ^{p,q}_\sigma (K)$
on
$B^{p,q}_\sigma (K)\subset \Lambda ^{p,q}_\sigma (K)$
on
![]() $\mathscr {A}_2$
. In fact, by Proposition 6.5 and Lemma 6.2(a), noticing that
$\mathscr {A}_2$
. In fact, by Proposition 6.5 and Lemma 6.2(a), noticing that
![]() $L^p(K)$
is contained in “
$L^p(K)$
is contained in “
![]() $\Lambda ^{p,\infty }_0(K)$
,” we can simply cover a large portion of
$\Lambda ^{p,\infty }_0(K)$
,” we can simply cover a large portion of
![]() $\mathscr {A}_2$
, see an illustration in Figure 8. However, it remains unclear for the strip region near
$\mathscr {A}_2$
, see an illustration in Figure 8. However, it remains unclear for the strip region near
![]() $p=1$
, if
$p=1$
, if
![]() $\mathscr {C}$
and
$\mathscr {C}$
and
![]() $\mathscr {L}_1$
intersect at some point with
$\mathscr {L}_1$
intersect at some point with
![]() $p>1$
. We will apply another idea to overcome this. Also, we mention here that a similar method can solve the
$p>1$
. We will apply another idea to overcome this. Also, we mention here that a similar method can solve the
![]() $\mathscr {A}_1$
region as well with necessary modifications.
$\mathscr {A}_1$
region as well with necessary modifications.

Figure 8: A portion of
![]() $\mathscr A_2$
.
$\mathscr A_2$
.
We will rely on Proposition 4.4 in this part, which says, for
![]() $0<\sigma <\mathscr L_1(p)$
, it holds that
$0<\sigma <\mathscr L_1(p)$
, it holds that
To get a reasonable estimate for
![]() $\big \|\tilde {E}[f|\Lambda _m]\big \|_{L^p(K)}$
, we start with a new decomposition.
$\big \|\tilde {E}[f|\Lambda _m]\big \|_{L^p(K)}$
, we start with a new decomposition.
Definition 6.6 (a). For
![]() $m\geq 0$
, we define
$m\geq 0$
, we define
![]() $T_m=\left \{\sum _{w\in \Lambda _m}h_w\circ F_w^{-1}:h_w\in \mathcal {H}_0, \forall w\in \Lambda _m\right \}$
.
$T_m=\left \{\sum _{w\in \Lambda _m}h_w\circ F_w^{-1}:h_w\in \mathcal {H}_0, \forall w\in \Lambda _m\right \}$
.
(b). Write
![]() $P_{T_m}$
for the orthogonal projection
$P_{T_m}$
for the orthogonal projection
![]() $L^2(K)\to T_m$
for
$L^2(K)\to T_m$
for
![]() $m\geq 0$
, and
$m\geq 0$
, and
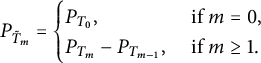 $$\begin{align*}{P}_{\tilde T_m}=\begin{cases} P_{T_0},&\text{ if }m=0,\\ P_{T_m}-P_{T_{m-1}},&\text{ if }m\geq 1. \end{cases} \end{align*}$$
$$\begin{align*}{P}_{\tilde T_m}=\begin{cases} P_{T_0},&\text{ if }m=0,\\ P_{T_m}-P_{T_{m-1}},&\text{ if }m\geq 1. \end{cases} \end{align*}$$
Since
![]() $P_{T_m}$
is realized by integration against an
$P_{T_m}$
is realized by integration against an
![]() $L^2$
orthogonal basis of harmonic functions, which are bounded, it extends to a bounded linear map
$L^2$
orthogonal basis of harmonic functions, which are bounded, it extends to a bounded linear map
![]() $L^p(K)\to T_m$
for any
$L^p(K)\to T_m$
for any
![]() $1\leq p\leq \infty $
.
$1\leq p\leq \infty $
.
(c). Write
![]() $\tilde {T}_m=\left \{P_{\tilde T_m}f:f\in L^1(K)\right \}$
for
$\tilde {T}_m=\left \{P_{\tilde T_m}f:f\in L^1(K)\right \}$
for
![]() $m\geq 1$
, and write
$m\geq 1$
, and write
![]() $\tilde {T}_0=T_0$
.
$\tilde {T}_0=T_0$
.
Remark The spaces
![]() $T_m$
are collections of piecewise harmonic functions, but may not be continuous at
$T_m$
are collections of piecewise harmonic functions, but may not be continuous at
![]() $V_{\Lambda _m}\setminus V_0$
.
$V_{\Lambda _m}\setminus V_0$
.
We collect some useful results in the following lemma.
Lemma 6.7 Let
![]() $1<p<\infty $
,
$1<p<\infty $
,
![]() $m\geq 0$
and
$m\geq 0$
and
![]() $u\in \tilde {T}_m$
.
$u\in \tilde {T}_m$
.
(a). We have
![]() $\tilde {E}[u|\Lambda _n]=0$
if
$\tilde {E}[u|\Lambda _n]=0$
if
![]() $n<m$
.
$n<m$
.
(b). For any
![]() $0<\sigma <\mathscr {C}(p)$
, we have
$0<\sigma <\mathscr {C}(p)$
, we have
![]() $\big \|\tilde {E}[u|\Lambda _n]\big \|_{L^p(K)}\lesssim r^{(n-m)\sigma d_W/2}\|u\|_{L^p(K)}$
for
$\big \|\tilde {E}[u|\Lambda _n]\big \|_{L^p(K)}\lesssim r^{(n-m)\sigma d_W/2}\|u\|_{L^p(K)}$
for
![]() ${n\geq m}$
.
${n\geq m}$
.
Proof (a). By definition, for each
![]() $u\in \tilde {T}_m$
, we have
$u\in \tilde {T}_m$
, we have
![]() $P_{T_{m-1}}u=0$
. On the other hand, we can see that
$P_{T_{m-1}}u=0$
. On the other hand, we can see that
![]() $\oplus _{l=0}^n \tilde {J}_l\subset T_{m-1}$
since clearly
$\oplus _{l=0}^n \tilde {J}_l\subset T_{m-1}$
since clearly
![]() $\tilde {J}_l$
consists of piecewise constant functions. Thus,
$\tilde {J}_l$
consists of piecewise constant functions. Thus,
(b). We first look at
![]() $m=0$
case. By definition of
$m=0$
case. By definition of
![]() $\mathscr {C}$
, we have
$\mathscr {C}$
, we have
![]() $r^{-n\sigma d_W/2}I_p(u,r^n)\lesssim \|u\|_{L^p(K)}$
, as
$r^{-n\sigma d_W/2}I_p(u,r^n)\lesssim \|u\|_{L^p(K)}$
, as
![]() $u\in \tilde {T}_m=\mathcal {H}_0$
. The claim then follows by applying Lemma 4.3(a).
$u\in \tilde {T}_m=\mathcal {H}_0$
. The claim then follows by applying Lemma 4.3(a).
For general case, for each
![]() $w\in \Lambda _m$
, we can see that
$w\in \Lambda _m$
, we can see that
(b) then follows by scaling and summing the estimates over
![]() $\Lambda _m$
.
$\Lambda _m$
.
Proposition 6.8 For
![]() $1<p<\infty $
,
$1<p<\infty $
,
![]() $1\leq q\leq \infty $
and
$1\leq q\leq \infty $
and
![]() $(\frac {1}{p},\sigma )\in \mathscr {A}_2$
, we have
$(\frac {1}{p},\sigma )\in \mathscr {A}_2$
, we have
![]() $B^{p,q}_\sigma (K)\subset \Lambda ^{p,q}_\sigma (K)$
with
$B^{p,q}_\sigma (K)\subset \Lambda ^{p,q}_\sigma (K)$
with
![]() $\|\cdot \|_{\Lambda ^{p,q}_\sigma (K)}\lesssim \|\cdot \|_{B^{p,q}_\sigma (K)}$
.
$\|\cdot \|_{\Lambda ^{p,q}_\sigma (K)}\lesssim \|\cdot \|_{B^{p,q}_\sigma (K)}$
.
Proof Let
![]() $f\in B^{p,q}_\sigma (K)$
, it suffices to show that
$f\in B^{p,q}_\sigma (K)$
, it suffices to show that
![]() $\big \|r^{-m\sigma d_W/2}\|\tilde {E}[f|\Lambda _m]\|_{L^p(K)}\big \|_{l^q}\lesssim \|f\|_{B^{p,q}_\sigma (K)}$
by applying Proposition 4.4.
$\big \|r^{-m\sigma d_W/2}\|\tilde {E}[f|\Lambda _m]\|_{L^p(K)}\big \|_{l^q}\lesssim \|f\|_{B^{p,q}_\sigma (K)}$
by applying Proposition 4.4.
For convenience, we write
![]() $\mathscr {P}:L^p(K)\to \prod _{m=0}^\infty \tilde {T}_m$
, defined as
$\mathscr {P}:L^p(K)\to \prod _{m=0}^\infty \tilde {T}_m$
, defined as
![]() $\mathscr {P}(f)_m=P_{\tilde T_m}f$
. Also, we equip each
$\mathscr {P}(f)_m=P_{\tilde T_m}f$
. Also, we equip each
![]() $\tilde {T}_m$
with the
$\tilde {T}_m$
with the
![]() $L^p$
norm. Then,
$L^p$
norm. Then,
![]() $P_{T_m}$
and
$P_{T_m}$
and
![]() $P_{\tilde T_m}$
are bounded linear maps on
$P_{\tilde T_m}$
are bounded linear maps on
![]() $L^p(K)$
, which immediately provides Claim 1.
$L^p(K)$
, which immediately provides Claim 1.
Claim 1
![]() $\mathscr {P}$
is bounded from
$\mathscr {P}$
is bounded from
![]() $L^p(K)$
to
$L^p(K)$
to
![]() $l^\infty (\tilde {T}_\cdot )$
.
$l^\infty (\tilde {T}_\cdot )$
.
Recall the definition of
![]() $l^p_\alpha $
from Lemma 6.1.
$l^p_\alpha $
from Lemma 6.1.
Claim 2
![]() $\mathscr {P}$
is bounded from
$\mathscr {P}$
is bounded from
![]() $H^p_2(K)$
to
$H^p_2(K)$
to
![]() $l^\infty _{r^{d_W}}(\tilde {T}_\cdot )$
.
$l^\infty _{r^{d_W}}(\tilde {T}_\cdot )$
.
Proof Let G be the Dirichlet Green’s operator on K [Reference Kigami26, Reference Strichartz36]. For any
![]() $f\in H^p_2(K)=H^p_{2,D}(K)\oplus \mathcal {H}_0$
, we have
$f\in H^p_2(K)=H^p_{2,D}(K)\oplus \mathcal {H}_0$
, we have
where the first inequality is due to the fact that
![]() $f-G(-\Delta ) f\in T_0=\mathcal {H}_0$
, and the second inequality is due to the fact that G is bounded from
$f-G(-\Delta ) f\in T_0=\mathcal {H}_0$
, and the second inequality is due to the fact that G is bounded from
![]() $L^p(K)$
to
$L^p(K)$
to
![]() $L^p(K)$
. We apply the above estimate locally on each
$L^p(K)$
. We apply the above estimate locally on each
![]() $F_wK$
with
$F_wK$
with
![]() $w\in \Lambda _m$
to get
$w\in \Lambda _m$
to get
by using the scaling property of
![]() $\Delta f$
. Thus, we have
$\Delta f$
. Thus, we have
This finishes the proof of Claim 2.
Combining Claim 1 and Claim 2, and using Lemma 6.1, we see the following claim.
Claim 3 For
![]() $1<p<\infty $
,
$1<p<\infty $
,
![]() $1\leq q\leq \infty $
and
$1\leq q\leq \infty $
and
![]() $0<\sigma <2$
,
$0<\sigma <2$
,
![]() $\mathscr {P}$
is bounded from
$\mathscr {P}$
is bounded from
![]() $B^{p,q}_\sigma (K)$
to
$B^{p,q}_\sigma (K)$
to
![]() $l^q_{r^{\sigma d_W/2}}(\tilde {T}_\cdot )$
.
$l^q_{r^{\sigma d_W/2}}(\tilde {T}_\cdot )$
.
Now, we turn to the proof of the proposition. We fix a parameter point
![]() $(\frac 1p, \sigma )$
in
$(\frac 1p, \sigma )$
in
![]() $\mathscr A_2$
. By Claim 3, we can see that, for each
$\mathscr A_2$
. By Claim 3, we can see that, for each
![]() $f\in B^{p,q}_\sigma (K),$
we clearly have
$f\in B^{p,q}_\sigma (K),$
we clearly have
![]() $f=\sum _{m=0}^\infty P_{\tilde T_m}f$
, with the series absolute convergent in
$f=\sum _{m=0}^\infty P_{\tilde T_m}f$
, with the series absolute convergent in
![]() $L^p(K)$
. Thus, we have
$L^p(K)$
. Thus, we have
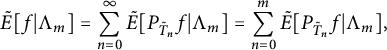 $$\begin{align*}\tilde{E}[f|\Lambda_m]=\sum_{n=0}^\infty \tilde{E}[P_{\tilde T_n}f|\Lambda_m]=\sum_{n=0}^m \tilde{E}[P_{\tilde T_n}f|\Lambda_m],\end{align*}$$
$$\begin{align*}\tilde{E}[f|\Lambda_m]=\sum_{n=0}^\infty \tilde{E}[P_{\tilde T_n}f|\Lambda_m]=\sum_{n=0}^m \tilde{E}[P_{\tilde T_n}f|\Lambda_m],\end{align*}$$
where the second equality is due to Lemma 6.7(a). In addition, by applying Lemma 6.7(b), we have the estimate
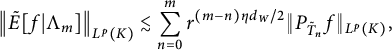 $$\begin{align*}\left\|\tilde{E}[f|\Lambda_m]\right\|_{L^p(K)}\lesssim \sum_{n=0}^m r^{(m-n)\eta d_W/2}\|P_{\tilde T_n}f\|_{L^p(K)},\end{align*}$$
$$\begin{align*}\left\|\tilde{E}[f|\Lambda_m]\right\|_{L^p(K)}\lesssim \sum_{n=0}^m r^{(m-n)\eta d_W/2}\|P_{\tilde T_n}f\|_{L^p(K)},\end{align*}$$
where
![]() $\eta $
is a fixed number such that
$\eta $
is a fixed number such that
![]() $\sigma <\eta <\mathscr {C}(p)$
. As a consequence, we then have
$\sigma <\eta <\mathscr {C}(p)$
. As a consequence, we then have
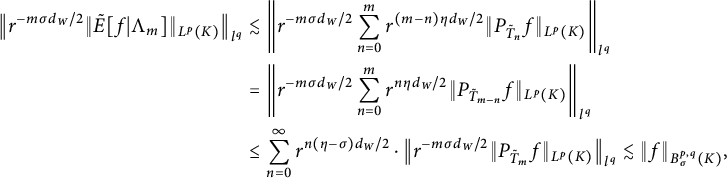 $$\begin{align*}\begin{aligned} \left\|r^{-m\sigma d_W/2}\|\tilde{E}[f|\Lambda_m]\|_{L^p(K)}\right\|_{l^q}&\lesssim \left\|r^{-m\sigma d_W/2}\sum_{n=0}^m r^{(m-n)\eta d_W/2}\|P_{\tilde T_n}f\|_{L^p(K)}\right\|_{l^q}\\ &= \left\|r^{-m\sigma d_W/2}\sum_{n=0}^m r^{n\eta d_W/2}\|P_{\tilde T_{m-n}}f\|_{L^p(K)}\right\|_{l^q}\\ &\leq \sum_{n=0}^\infty r^{n(\eta-\sigma)d_W/2}\cdot\left\|r^{-m\sigma d_W/2}\|P_{\tilde T_m}f\|_{L^p(K)}\right\|_{l^q}\lesssim \|f\|_{B^{p,q}_\sigma(K)}, \end{aligned}\end{align*}$$
$$\begin{align*}\begin{aligned} \left\|r^{-m\sigma d_W/2}\|\tilde{E}[f|\Lambda_m]\|_{L^p(K)}\right\|_{l^q}&\lesssim \left\|r^{-m\sigma d_W/2}\sum_{n=0}^m r^{(m-n)\eta d_W/2}\|P_{\tilde T_n}f\|_{L^p(K)}\right\|_{l^q}\\ &= \left\|r^{-m\sigma d_W/2}\sum_{n=0}^m r^{n\eta d_W/2}\|P_{\tilde T_{m-n}}f\|_{L^p(K)}\right\|_{l^q}\\ &\leq \sum_{n=0}^\infty r^{n(\eta-\sigma)d_W/2}\cdot\left\|r^{-m\sigma d_W/2}\|P_{\tilde T_m}f\|_{L^p(K)}\right\|_{l^q}\lesssim \|f\|_{B^{p,q}_\sigma(K)}, \end{aligned}\end{align*}$$
where we use Claim 3 again in the last inequality.
Remark We can apply a similar argument as Lemma 6.7 and Proposition 6.8 for
![]() $(\frac 1p,\sigma )\in \mathscr B$
to show that
$(\frac 1p,\sigma )\in \mathscr B$
to show that
![]() $B^{p,q}_\sigma (K)\subset \Lambda ^{p,q}_{\sigma ,(1)}(K)$
, as stated in Proposition 6.5. The difference is that
$B^{p,q}_\sigma (K)\subset \Lambda ^{p,q}_{\sigma ,(1)}(K)$
, as stated in Proposition 6.5. The difference is that
![]() $f_m\in J_m$
in the tent function expansion of
$f_m\in J_m$
in the tent function expansion of
![]() $f=\sum _{m=0}^\infty f_m$
depends on
$f=\sum _{m=0}^\infty f_m$
depends on
![]() $P_{\tilde T_n}f$
for
$P_{\tilde T_n}f$
for
![]() $n\geq m$
. This gives a second proof of Proposition 6.5.
$n\geq m$
. This gives a second proof of Proposition 6.5.
We finish this section with a conclusion that Theorem 1.1 holds.
Proof of Theorem 1.1
On
![]() $\mathscr {A}_1$
, the theorem follows from Proposition 6.5; on
$\mathscr {A}_1$
, the theorem follows from Proposition 6.5; on
![]() $\mathscr {A}_2$
, the theorem follows from Propositions 5.3 and 6.8; lastly, on the border between
$\mathscr {A}_2$
, the theorem follows from Propositions 5.3 and 6.8; lastly, on the border between
![]() $\mathscr {A}_1$
and
$\mathscr {A}_1$
and
![]() $\mathscr {A}_2$
, we have
$\mathscr {A}_2$
, we have
![]() $B^{p,q}_\sigma (K)\subset \Lambda ^{p,q}_\sigma (K)$
by interpolation using Lemma 6.2(a), as well as the other direction is covered by Proposition 5.3. Finally, the region is sharp by Proposition 3.2.
$B^{p,q}_\sigma (K)\subset \Lambda ^{p,q}_\sigma (K)$
by interpolation using Lemma 6.2(a), as well as the other direction is covered by Proposition 5.3. Finally, the region is sharp by Proposition 3.2.
Acknowledgment
The authors are very grateful to Professor Robert S. Strichartz who introduced them to this problem and gave them constant help in this work. The authors appreciate the anonymous referees for their careful proofreading and valuable comments. The authors also thank Mr. Lijian Yang for providing the figures.