Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-15T01:59:53.475Z Has data issue: false hasContentIssue false
  • English
  • Français

Convergence of Classes of Amarts Indexed by Directed Sets

Published online by Cambridge University Press:  20 November 2018

Annie Millet  and
Louis Sucheston
Annie Millet
Affiliation:
Ohio State University Columbus, Ohio
Louis Sucheston
Affiliation:
Ohio State University Columbus, Ohio
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 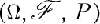be a probability space, J a directed set filtering to the right. (X t) t∈J is a family of random variables adapted to an increasing family of σ-algebras 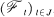. Vitali conditions V and V' on the σ-algebras, abstracting classical assumptions in Lebesgue's derivation theory, were made to insure essential convergence of martingales and submartingales (under proper boundedness assumptions). In reality these conditions, guaranteeing the existence of certain disjoint and properly measurable sets Bi, are better suited for study of amarts, since the sets Bi are a natural habitat and breeding ground for stopping times, thriving, as well known, precisely on disjoint and properly measurable sets. Thus K. Astbury [1] showed that the condition V, proved by K. Krickeberg to be sufficient for convergence of martingales (see [20] or Neveu [26], p. 98) is both necessary and sufficient for convergence of amarts. (We follow Neveu denoting by V the condition Krickeberg denotes by V+∞.) The Vitali condition V’, proved by Krickeberg [21] to be sufficient for convergence of submartingales, is shown here to be both necessary and sufficient for convergence of ordered amarts, defined similarly to amarts, except that the stopping times are ordered. We also introduce the controlled Vitali condition Ve, properly weaker than V’, and show that Ve is sufficient for convergence of controlled amarts, including submartingales.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 32 , Issue 1 , 01 February 1980 , pp. 86 - 125
Copyright
Copyright © Canadian Mathematical Society 1980

References

1. Astbury, K., On Amarts and other topics, Ph.D. Dissertation, Ohio State University, (1976). Also Amarts indexed by directed sets, Ann. Prob. 6 (1978), 267–278.Google Scholar
2. Austin, D. G., Edgar, G. A. and Ionescu Tulcea, A., Pointwise convergence in terms of expectations, Zeit. Wahrscheinlichkeitstheorie verw. Gebiet. 30 (1974), 17–26.Google Scholar
3. Baxter, J. R., Pointwise in terms of weak convergence, Proc. Amer. Math. Soc. 46 (1974), 395–398.Google Scholar
4. Bellow, A., Les amarts uniformes, C.R. Acad. Sci. Paris 284, Série A, 1295-1298.Google Scholar
5. Brunei, A. and Sucheston, L., Sur les amarts à valeurs vectorielles, C.R. Acad. Sci. Paris, Série A, 283, 1037–1039.Google Scholar
6. Chacon, R. V., A stopped proof of convergence, Adv. in Math. 14 (1974) 365–368.Google Scholar
7. Chacon, R. V. and Sucheston, L., On convergence of vector-valued asymptotic martingales, Zeit. Wahrscheinlichkeitstheorie verw. Gebiet. 33 (1975), 55–59.Google Scholar
8. Chatterji, S. D., Martingale convergence and the Radon-Nikodym theorem, Math. Scand. 22 (1968), 21–41.Google Scholar
9. Dieudonné, J., Sur un théorème de lessen, Fund. Math. 37 (1950), 242–248.Google Scholar
10. Doob, J. L., Stochastic processes (Wiley, New York, 1953).Google Scholar
11. Dvoretzky, A., On stopping times directed convergence, Bull. Amer. Math. Soc. 82, No. 2 (1976), 347–349.Google Scholar
12. Edgar, G. A. and Sucheston, L., Amarts: A class of asymptotic martingales, J. Multivariate Anal. 6 (1976), 193–221; 572-591.Google Scholar
13. Edgar, G. A. and Sucheston, L., The Riesz decomposition for vector-valued amarts, Zeit. Wahrscheinlichkeitstheorie verw. Gebiet. 36 (1976), 85–92.Google Scholar
14. Edgar, G. A. and Sucheston, L., On vector-valued amarts and dimension of Banach spaces, Zeit. Wahrscheinlichkeitstheorie verw. Gebiet. 39 (1977), 213–216.Google Scholar
15. Edgar, G. A. and Sucheston, L., Martingales in the limit and amarts, Proc. Amer. Math. Soc. 67 (1977), 315–320.Google Scholar
16. Ghoussoub, N. and Sucheston, L., A Refinement of the Riesz decomposition for amarts and semi amarts, J. Multivariate Analysi. 8 (1978), 146–150.Google Scholar
17. Hayes, C. A. and Pauc, C. Y., Derivations and martingales (Springer-Verlag, New York, 1970).Google Scholar
18. Helms, L. L., Mean convergence 0﹜ martingales, Trans. Amer. Math. Soc. 87 (1958), 439–446.Google Scholar
19. Krengel, U. and Sucheston, L., On semiamarts, amarts, and processes with finite value, Advances in Probabilit. 4 (1978), 197–266.Google Scholar
20. Krickeberg, K., Convergence of martingales with a directed index set, Trans. Amer. Math. Soc. 83 (1956), 313–337.Google Scholar
21. Krickeberg, K., Stochastische Konvergenz von Semimartingalen, Math. Z. 66 (1957), 470–486.Google Scholar
22. Krickeberg, K., Notwendige Konvergenzbedingungen bei Martingalen und verwandten Prozessen, Transactions of the Second Prague conference on information theory, statistical decision functions, random processes [1959 Prague], (1960), 279–305 (Prague, Publishing House of the Czechoslovak Academy of Sciences).Google Scholar
23. Krickeberg, K. and Pauc, C., Martingales et dérivation, Bull. Soc. Math. Franc. 91 (1963), 455–544.Google Scholar
24. Lamb, Ch., A ratio limit theorem for approximate martingales, Can. J. Math. 25 (1973), 772–779.Google Scholar
25. Mucci, A. G., Another Martingale convergence theorem, Pacific J. Math. 64 (1976), 539–541.Google Scholar
26. Neveu, J., Discrete parameter martingales (North Holland, Amsterdam, 1975).Google Scholar
27. Royden, H. L., Real analysis (Macmillan Company, N.Y., 1968).Google Scholar
28. Rudin, W., Real and complex analysis (McGraw-Hill, 1970).Google Scholar
29. Sucheston, L., On existence of finite invariant measures, Math. Z. 86 (1964), 327–336.Google Scholar
30. Yosida, K. and Hewitt, E., Finitely additive measures, Trans. Amer. Math. Soc. 72 (1952), 46–66.Google Scholar