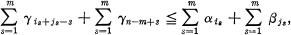Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Thompson, R.C.
1975.
Singular value inequalities for matrix sums and minors.
Linear Algebra and its Applications,
Vol. 11,
Issue. 3,
p.
251.
Cain, Bryan E.
and
Marques de Sá, E.
1981.
The inertia of a Hermitian matrix having prescribed complementary principal submatrices.
Linear Algebra and its Applications,
Vol. 37,
Issue. ,
p.
161.
Sharma, C.S.
1985.
A simple proof of the inequality of Thompson and Therianos concerning sums of eigenvalues of a hermitian matrix.
Physics Letters A,
Vol. 111,
Issue. 6,
p.
261.
Horn, Roger A.
Rhee, Noah H.
and
Wasin, So
1998.
Eigenvalue inequalities and equalities.
Linear Algebra and its Applications,
Vol. 270,
Issue. 1-3,
p.
29.
Savchenko, S.V.
2006.
Normal matrices and their principal submatrices of co-order one.
Linear Algebra and its Applications,
Vol. 419,
Issue. 2-3,
p.
556.
Huang, X.
and
Ghodsi, M.
2016.
A novel mutual association measure based on eigenvalue-based criterion.
International Journal of Energy and Statistics,
Vol. 04,
Issue. 04,
p.
1650017.




 denote the eigenvalues of
denote the eigenvalues of