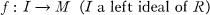Research Article
Involutory Matrices Over Finite Local Rings
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 369-378
-
- Article
-
- You have access
- Export citation
Generalization of Watson's Lemma
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 185-208
-
- Article
-
- You have access
- Export citation
Absolute Continuity of Some Vector Functions and Measures
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 737-746
-
- Article
-
- You have access
- Export citation
A Class of Non-Central E-Functors
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1-4
-
- Article
-
- You have access
- Export citation
Certain Artinian Rings are Noetherian
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 553-556
-
- Article
-
- You have access
- Export citation
Graphical Regular Representations of Non-Abelian Groups, I
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 993-1008
-
- Article
-
- You have access
- Export citation
Rings with Finite Norm Property
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 557-565
-
- Article
-
- You have access
- Export citation
Uniformities on a Product
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 379-389
-
- Article
-
- You have access
- Export citation
Graphical Regular Representations of Non-Abelian Groups, II
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1009-1018
-
- Article
-
- You have access
- Export citation
Polynomes a Valeurs Entieres
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 747-754
-
- Article
-
- You have access
- Export citation
Compact Induced Representations
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 5-16
-
- Article
-
- You have access
- Export citation
Injectivity in Equational Classes of Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 209-220
-
- Article
-
- You have access
- Export citation
Conjugate p-Subgroups of Finite Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 17-28
-
- Article
-
- You have access
- Export citation
On Strong Nörlund Summability Fields
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 390-399
-
- Article
-
- You have access
- Export citation
Cohomology Theorems for Borel-Like Solvable Lie Algebras in Arbitrary Characteristic
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1019-1026
-
- Article
-
- You have access
- Export citation
Integral Means and Zero Distributions of Blaschke Products
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 755-760
-
- Article
-
- You have access
- Export citation
Radicals of PID's and Dedekind Domains
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 566-572
-
- Article
-
- You have access
- Export citation
The Augmentation Terminals of Certain Locally Finite Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 221-238
-
- Article
-
- You have access
- Export citation
𝔪-Stone Lattices
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1027-1032
-
- Article
-
- You have access
- Export citation
Galois Theory of Essential Extensions of Modules
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 573-579
-
- Article
-
- You have access
- Export citation



 of left, unitary R-modules the Hochschild
of left, unitary R-modules the Hochschild  wherever this series converges. (Where no limits are stated, sums are throughout to be taken from
wherever this series converges. (Where no limits are stated, sums are throughout to be taken from 

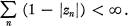
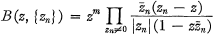
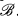 . If
. If 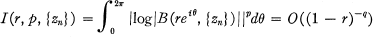

 otherwise. The first ordinal λ for which g
otherwise. The first ordinal λ for which g