Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-28T00:43:06.983Z Has data issue: false hasContentIssue false
  • English
  • Français

Familles De Valuations A Caractere Compact

Published online by Cambridge University Press:  20 November 2018

Cécile M. Wong
Cécile M. Wong*
Affiliation:
Université de Montréal, Montréal, P.Q.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Soit Ω une famille de valuations d'un corps commutatif K. Dénotons par 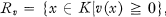, l'anneau de la valuation v, et Mv =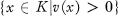, l'idéal maximal de l'anneau Rv. Soit 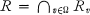l'anneau défini par la famille Ω; nous supposons toujours Ω tel que K soit le corps des fractions de R, et tel que Rv ≠ Rw dès que v ≠ w (v et w ∈ Ω).

Pour tout x ∈ K, posons 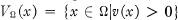et munissons Ω de la topologie la plus faible pour laquelle les VΩ(X) sont des ouverts. On dit que la famille Ω est à caractère compact (respectivement, fini) si pour chaque élément non nul x de K, VΩ(X) est quasi compact (respectivement, est un ensemble fini). S'il n'y a pas de confusion possible quant à la famille Ω, on écrit V(x) plutôt que VΩ(X).

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 24 , Issue 3 , June 1972 , pp. 416 - 425
Copyright
Copyright © Canadian Mathematical Society 1972

References

Bibliographie

1. Malcolm, Griffin, Some results on v-multiplication rings, Can. J. Math. 19 (1967), 710–722.Google Scholar
2. Malcolm, Griffin, Families of finite character and essential valuations, Trans. Amer. Math. Soc. 130 (1968), 75–86.Google Scholar
3. Malcolm, Griffin, Rings of Krull type, J. reine angew. Math. 229 (1968), 1–28.Google Scholar
4. Wolfgang, Krull, Idealtheorie in unendlichen algebraischer Zahlkörpern. II, Math. Z. 31 (1930), 527–557.Google Scholar
5. Wolfgang, Krull, Beiträge zur Arithmetik kommutativer Integritätsbereiche IV: Unendliche algebraische Erweiterungen endlicher diskreter Hauptordnungen, Math. Z. 43 (1937), 767–773.Google Scholar
6. Wolfgang, Krull, Charakterentopologie, Isomorphismentopologie und Bewertungstopologie, Memoria de Matematica des Institute “Jorge Juan”, 1955.Google Scholar
7. Wong, Cécile M., Théorèmes d'approximation pour les familles de valuations à caractère compact (article en préparation).Google Scholar
8. Paulo, Ribenboim, Modules sur un anneau de Dedekind, Summa Bras. Math. 3 (1952), 21–37.Google Scholar
9. Paulo, Ribenboim, Anneaux normaux réels à caractère fini, Summa Bras. Math. 3 (1956), 213–254.Google Scholar
10. Paulo, Ribenboim, Théorie des valuations (Les Presses de l'Université de Montréal, 1964).Google Scholar