Published online by Cambridge University Press: 20 November 2018
Let G be a lattice-ordered group (l-group). If X ⊆ G, then let
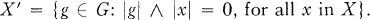
Then X’ is a convex l-subgroup of G called a polar. The set P(G) of all polars of G is a complete Boolean algebra with ‘ as complementation and set-theoretic intersection as meet. An l-subgroup H of G is large in G (G is an essential extension of H) if each non-zero convex l-subgroup of G has non-trivial intersection with H. If these l-groups are archimedean, it is enough to require that each non-zero polar of G meets H. This implies that the Boolean algebras of polars of G and H are isomorphic. If K is a cardinal summand of G, then K is a polar, and we write G = K⊞K'.