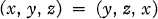Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Dorofeev, G. V.
1973.
Centers of nonassociative rings.
Algebra and Logic,
Vol. 12,
Issue. 5,
p.
297.
Kleinfeld, Erwin
and
Widmer, Lamarr
1989.
Rings satisfying (x,y,z) = (y,z,x).
Communications in Algebra,
Vol. 17,
Issue. 11,
p.
2683.
Schafer, R.D
1992.
On semialternative algebras.
Journal of Algebra,
Vol. 152,
Issue. 1,
p.
259.
Vakhitov, R. Kh.
1993.
Alternator ideal in weakly alternative rings.
Algebra and Logic,
Vol. 32,
Issue. 3,
p.
133.
Vakhitov, R. Kh.
1994.
Associator-cyclic bimodules.
Mathematical Notes,
Vol. 56,
Issue. 5,
p.
1113.
Bremner, Murray
1999.
On the Z-module structure of a free semialternative ring.
Communications in Algebra,
Vol. 27,
Issue. 4,
p.
1951.
Sánchez-Ortega, Juana
2013.
On the definitions of nucleus for dialgebras.
Journal of Algebra,
Vol. 392,
Issue. ,
p.
244.
Blachar, Guy
Rowen, Louis
and
Vishne, Uzi
2023.
Algebra and Coding Theory.
Vol. 785,
Issue. ,
p.
35.