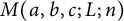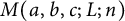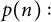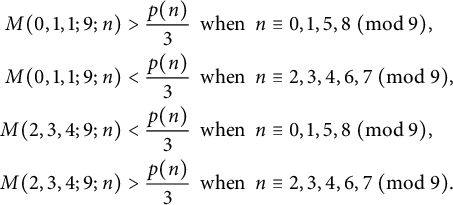1 Introduction
A partition of a positive integer n is a nonincreasing sequence of positive integers whose sum equals n. Typically,
![]() $p(n)$
is used to denote the number of partitions of
$p(n)$
is used to denote the number of partitions of
![]() $n.$
The generating function for
$n.$
The generating function for
![]() $p(n)$
is as follows:
$p(n)$
is as follows:
Here and in what follows,
![]() $|q| < 1,$
and
$|q| < 1,$
and
In 1944, Dyson [Reference Dyson12] defined the rank of a partition to be the largest part minus the number of parts. Let
![]() $N(m;n)$
be the number of partitions of n with rank m and
$N(m;n)$
be the number of partitions of n with rank m and
![]() $N(m,L;n)$
the number of partitions of n with rank congruent to m modulo
$N(m,L;n)$
the number of partitions of n with rank congruent to m modulo
![]() $L.$
Dyson conjectured that
$L.$
Dyson conjectured that
 $$ \begin{align*} \begin{aligned} N(a,5;5n+4) = \frac{p(5n+4)}{5}, \\ N(a,7;7n+5) = \frac{p(5n+4)}{7}, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} N(a,5;5n+4) = \frac{p(5n+4)}{5}, \\ N(a,7;7n+5) = \frac{p(5n+4)}{7}, \end{aligned} \end{align*} $$
which provide combinatorial proofs for the cases of modulo 5 and 7 in Ramanujan’s congruences. In addition, Dyson conjectured that there exists a crank function for partitions which would supply a combinatorial proof of Ramanujan’s congruences modulo 11. In 1954, Atkin and Swinnerton-Dyer [Reference Atkin and Swinnerton-Dyer5] proved the above identities of Dyson by applying the generating function for
![]() $N(m,L;n).$
$N(m,L;n).$
Forty years later, Andrews and Garvan [Reference Andrews and Garvan3] defined the crank function for partitions. Let
![]() $M(m;n)$
be the number of partitions of n with crank m and let
$M(m;n)$
be the number of partitions of n with crank m and let
![]() $M(m,L;n)$
be the number of partitions of n with crank congruent to m modulo
$M(m,L;n)$
be the number of partitions of n with crank congruent to m modulo
![]() $L.$
Andrews and Garvan proved that
$L.$
Andrews and Garvan proved that
which provides a combinatorial proof for Ramanujan’s congruences modulo 11. Recently, many inequalities for
![]() $M(m,L;n)$
and
$M(m,L;n)$
and
![]() $N(m,L;n)$
modulo 11 were deduced by Borozenets [Reference Borozenets7] and Bringmann and Pandey [Reference Bringmann and Pandey8]. For inequalities between the rank counts
$N(m,L;n)$
modulo 11 were deduced by Borozenets [Reference Borozenets7] and Bringmann and Pandey [Reference Bringmann and Pandey8]. For inequalities between the rank counts
![]() $N(m,L;n)$
or between the crank counts
$N(m,L;n)$
or between the crank counts
![]() $M(m,L;n),$
see, for example, [Reference Andrews and Lewis1, Reference Chan and Mao10, Reference Chen, Chern, Fan and Xia11, Reference Mao16]. For distributions of rank and crank statistics for integer partitions, see, for example, [Reference Zhou20, Reference Zhou21].
$M(m,L;n),$
see, for example, [Reference Andrews and Lewis1, Reference Chan and Mao10, Reference Chen, Chern, Fan and Xia11, Reference Mao16]. For distributions of rank and crank statistics for integer partitions, see, for example, [Reference Zhou20, Reference Zhou21].
For convenience, we adopt the following notations:
 $$ \begin{align*} \begin{aligned} N(a,b,c;L;n)&:= N(a,L;n) + N(b,L;n) + N(c,L;n), \\ M(a,b,c;L;n)&:= M(a,L;n) + M(b,L;n) + M(c,L;n). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} N(a,b,c;L;n)&:= N(a,L;n) + N(b,L;n) + N(c,L;n), \\ M(a,b,c;L;n)&:= M(a,L;n) + M(b,L;n) + M(c,L;n). \end{aligned} \end{align*} $$
In [Reference Kang15, Theorem 4.1], Kang showed the following relationship between rank and crank:
 $$ \begin{align*} \begin{aligned} \sum_{m=-\infty}^{\infty} & \sum_{n=0}^{\infty} (N(3m-1;n)+N(3m;n)+N(3m+1;n))z^m q^n \\ = & \frac{(q^3;q^3)_{\infty}}{(q;q)_{\infty}}\sum_{m=-\infty}^{\infty}\sum_{n=0}^{\infty} M(m;n)z^m q^{3n}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \sum_{m=-\infty}^{\infty} & \sum_{n=0}^{\infty} (N(3m-1;n)+N(3m;n)+N(3m+1;n))z^m q^n \\ = & \frac{(q^3;q^3)_{\infty}}{(q;q)_{\infty}}\sum_{m=-\infty}^{\infty}\sum_{n=0}^{\infty} M(m;n)z^m q^{3n}. \end{aligned} \end{align*} $$
Inspired by this relationship, Aygin and Chan [Reference Aygin and Chan6] provided a series of generating functions for
![]() $M(a,b,c;L;n)$
. For
$M(a,b,c;L;n)$
. For
![]() $L \in \{6,9,12\}$
, Aygin and Chan found generating functions of
$L \in \{6,9,12\}$
, Aygin and Chan found generating functions of
 $$ \begin{align*} \begin{aligned} N(3j-1,3j,3j+1;L;n), \quad \mathrm{for} ~ 0\leq j \leq L/3 - 1, \\ M(3j-1,3j,3j+1;L;n), \quad \mathrm{for} ~ 0\leq j \leq L/3 - 1, \\ M(3j-2,3j-1,3j;L;n), \quad \mathrm{for} ~ 0\leq j \leq L/3 - 1 \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} N(3j-1,3j,3j+1;L;n), \quad \mathrm{for} ~ 0\leq j \leq L/3 - 1, \\ M(3j-1,3j,3j+1;L;n), \quad \mathrm{for} ~ 0\leq j \leq L/3 - 1, \\ M(3j-2,3j-1,3j;L;n), \quad \mathrm{for} ~ 0\leq j \leq L/3 - 1 \end{aligned} \end{align*} $$
and used the periodicity of the sign of the Fourier coefficients of these generating functions to prove many inequalities between
![]() $M(a,b,c;L;n)$
and the partition function
$M(a,b,c;L;n)$
and the partition function
![]() $p(n).$
At the end of the paper, they proposed 18 inequalities of such type as a conjecture. In [Reference Fan, Xia and Zhao13], Fan, Xia, and Zhao established some generating functions for
$p(n).$
At the end of the paper, they proposed 18 inequalities of such type as a conjecture. In [Reference Fan, Xia and Zhao13], Fan, Xia, and Zhao established some generating functions for
![]() $N(a,12;n)$
and
$N(a,12;n)$
and
![]() $M(a,12;n)$
with
$M(a,12;n)$
with
![]() $0 \leq a \leq 11$
, and used them to confirm the first 6 inequalities in the conjecture of Aygin and Chan. Later, Yao [Reference Yao19] proved that the remaining 12 inequalities hold for sufficiently large n. Simultaneously, at the end of their paper, Aygin and Chan said that “Additionally, the referee pointed out that the signs of theta parts of
$0 \leq a \leq 11$
, and used them to confirm the first 6 inequalities in the conjecture of Aygin and Chan. Later, Yao [Reference Yao19] proved that the remaining 12 inequalities hold for sufficiently large n. Simultaneously, at the end of their paper, Aygin and Chan said that “Additionally, the referee pointed out that the signs of theta parts of
![]() $M(0,1,1;9;n)$
,
$M(0,1,1;9;n)$
,
![]() $M(2,3,4;9;n)$
,
$M(2,3,4;9;n)$
,
![]() $M(0,1,2;9;n)$
,
$M(0,1,2;9;n)$
,
![]() $M(3,4,5;9;n)$
, and
$M(3,4,5;9;n)$
, and
![]() $M(6,7,8;9;n)$
are periodic modulo 9 when
$M(6,7,8;9;n)$
are periodic modulo 9 when
![]() $n \geq 467.$
Thus, conjectures similar to Conjecture 8.1 can be stated for
$n \geq 467.$
Thus, conjectures similar to Conjecture 8.1 can be stated for
![]() $M(0,1,1;9;n)$
,
$M(0,1,1;9;n)$
,
![]() $M(2,3,4;9;n)$
,
$M(2,3,4;9;n)$
,
![]() $M(0,1,2;9;n)$
,
$M(0,1,2;9;n)$
,
![]() $M(3,4,5;9;n)$
and
$M(3,4,5;9;n)$
and
![]() $M(6,7,8;9;n)$
.” Up to now, as far as we are concerned, no inequality for
$M(6,7,8;9;n)$
.” Up to now, as far as we are concerned, no inequality for
![]() $M(0,1,1;9;n)$
,
$M(0,1,1;9;n)$
,
![]() $M(2,3,4;9;n)$
,
$M(2,3,4;9;n)$
,
![]() $M(0,1,2;9;n)$
,
$M(0,1,2;9;n)$
,
![]() $M(3,4,5;9;n)$
and
$M(3,4,5;9;n)$
and
![]() $M(6,7,8;9;n),$
which is similar to [Reference Aygin and Chan6, Conjecture 8.1], has been proposed explicitly and proved.
$M(6,7,8;9;n),$
which is similar to [Reference Aygin and Chan6, Conjecture 8.1], has been proposed explicitly and proved.
In this paper, we state some inequalities for
![]() $M(0,1,1;9;n)$
and
$M(0,1,1;9;n)$
and
![]() $M(2,3,4;9;n)$
and prove them.
$M(2,3,4;9;n)$
and prove them.
Theorem 1.1 For
![]() $n \geq 467$
, we have
$n \geq 467$
, we have
 $$ \begin{align*} M(0,1,1;9;n)> \frac{p(n)}{3}&\;\: \mathrm{when}\;\: n \equiv 0,1,5,8 ~ (\mathrm{mod}~9), \\ M(0,1,1;9;n) < \frac{p(n)}{3}&\;\: \mathrm{when}\;\: n \equiv 2,3,4,6,7 ~ (\mathrm{mod}~9), \\ M(2,3,4;9;n) < \frac{p(n)}{3}&\;\: \mathrm{when}\;\: n \equiv 0,1,5,8 ~ (\mathrm{mod}~9), \\ M(2,3,4;9;n)> \frac{p(n)}{3}&\;\: \mathrm{when}\;\: n \equiv 2,3,4,6,7 ~ (\mathrm{mod}~9). \end{align*} $$
$$ \begin{align*} M(0,1,1;9;n)> \frac{p(n)}{3}&\;\: \mathrm{when}\;\: n \equiv 0,1,5,8 ~ (\mathrm{mod}~9), \\ M(0,1,1;9;n) < \frac{p(n)}{3}&\;\: \mathrm{when}\;\: n \equiv 2,3,4,6,7 ~ (\mathrm{mod}~9), \\ M(2,3,4;9;n) < \frac{p(n)}{3}&\;\: \mathrm{when}\;\: n \equiv 0,1,5,8 ~ (\mathrm{mod}~9), \\ M(2,3,4;9;n)> \frac{p(n)}{3}&\;\: \mathrm{when}\;\: n \equiv 2,3,4,6,7 ~ (\mathrm{mod}~9). \end{align*} $$
We will employ the modification [Reference Kane14] of the circle methodFootnote
1
to estimate the Fourier coefficients of generating functions for
![]() $M(0,1,1;9;n)$
and
$M(0,1,1;9;n)$
and
![]() $M(2,3,4;9;n)$
, obtaining information about the sign of the coefficients of
$M(2,3,4;9;n)$
, obtaining information about the sign of the coefficients of
![]() $g(q)-3h(q)$
(see (3.1) and (3.2) for the definitions of
$g(q)-3h(q)$
(see (3.1) and (3.2) for the definitions of
![]() $g(q)$
and
$g(q)$
and
![]() $h(q)$
), and thereby prove the inequalities in Theorem 1.1. An inequality for the logarithm of the generating function for
$h(q)$
), and thereby prove the inequalities in Theorem 1.1. An inequality for the logarithm of the generating function for
![]() $p(n)$
will be derived and used to reduce the last possible counterexamples to
$p(n)$
will be derived and used to reduce the last possible counterexamples to
![]() $467 \leq n \leq 22471.$
This method will produce more effective estimates when proving such types of inequalities.
$467 \leq n \leq 22471.$
This method will produce more effective estimates when proving such types of inequalities.
2 Preliminaries
For
![]() $f(s) = \sum _{n=0}^{\infty } \alpha (n) s^n$
, we apply the residue theorem to the generating function to get
$f(s) = \sum _{n=0}^{\infty } \alpha (n) s^n$
, we apply the residue theorem to the generating function to get
with r smaller than the convergence radius.
2.1 Splitting integral intervals with Farey fractions
We set
![]() $r :=e^{-2\pi \varrho }$
with
$r :=e^{-2\pi \varrho }$
with
![]() $\varrho =1/N^2$
for some
$\varrho =1/N^2$
for some
![]() $N>0$
. Let
$N>0$
. Let
![]() $h/k$
be a Farey fraction of order N, and let
$h/k$
be a Farey fraction of order N, and let
![]() $\xi _{h,k} := [-\theta _{h,k}^{\prime },\theta _{h,k}^{\prime \prime }]$
with
$\xi _{h,k} := [-\theta _{h,k}^{\prime },\theta _{h,k}^{\prime \prime }]$
with
![]() $\theta _{h,k}^{\prime },\theta _{h,k}^{\prime \prime }$
being the distance from
$\theta _{h,k}^{\prime },\theta _{h,k}^{\prime \prime }$
being the distance from
![]() $h/k$
to its neighboring mediants. If we set
$h/k$
to its neighboring mediants. If we set
and let
![]() $\theta := h/k + \varphi $
on each
$\theta := h/k + \varphi $
on each
![]() $\xi _{h,k}$
, then
$\xi _{h,k}$
, then
so that
 $$ \begin{align*} \alpha(n) = \sum_{\substack{0 \leq h<k \leq N \\ (h,k) = 1}} e^{-2\pi i nh/k} \int_{\xi_{h,k}} f(e^{2\pi i(h/k + i\varrho + \varphi)}) e^{2\pi n \varrho} e^{-2\pi i n \varphi} d\varphi. \end{align*} $$
$$ \begin{align*} \alpha(n) = \sum_{\substack{0 \leq h<k \leq N \\ (h,k) = 1}} e^{-2\pi i nh/k} \int_{\xi_{h,k}} f(e^{2\pi i(h/k + i\varrho + \varphi)}) e^{2\pi n \varrho} e^{-2\pi i n \varphi} d\varphi. \end{align*} $$
Set
![]() $z:=k(\varrho -i\varphi )$
and
$z:=k(\varrho -i\varphi )$
and
![]() $\tau :=(h+iz)/k$
to get
$\tau :=(h+iz)/k$
to get
 $$ \begin{align} \begin{aligned} \alpha(n) &= \sum_{\substack{0 \leq h<k \leq N \\ (h,k) = 1}} e^{-2\pi i nh/k} \int_{\xi_{h,k}} f(e^{2\pi i(h+iz)/k}) e^{2\pi n \varrho} e^{-2\pi i n \varphi} d\varphi \\ &= \sum_{\substack{0 \leq h<k \leq N \\ (h,k) = 1}} e^{-2\pi i nh/k} \int_{\xi_{h,k}} f(e^{2\pi i \tau}) e^{2\pi n \varrho} e^{-2\pi i n \varphi} d\varphi. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \alpha(n) &= \sum_{\substack{0 \leq h<k \leq N \\ (h,k) = 1}} e^{-2\pi i nh/k} \int_{\xi_{h,k}} f(e^{2\pi i(h+iz)/k}) e^{2\pi n \varrho} e^{-2\pi i n \varphi} d\varphi \\ &= \sum_{\substack{0 \leq h<k \leq N \\ (h,k) = 1}} e^{-2\pi i nh/k} \int_{\xi_{h,k}} f(e^{2\pi i \tau}) e^{2\pi n \varrho} e^{-2\pi i n \varphi} d\varphi. \end{aligned} \end{align} $$
2.2 Dedekind’s eta-function
The Dedekind eta-function is defined by
where
![]() $q=e^{2\pi i \tau }$
with
$q=e^{2\pi i \tau }$
with
![]() $\mathrm {Im}(\tau )> 0.$
A well-known transformation formula for the Dedekind eta-function is as follows [Reference Apostol4, p. 52].
$\mathrm {Im}(\tau )> 0.$
A well-known transformation formula for the Dedekind eta-function is as follows [Reference Apostol4, p. 52].
For
 $\gamma = \left (\begin {matrix} a & b \\ c & d \end {matrix}\right ) \in \varGamma :=\mathrm {SL}_2(\mathbb {Z})$
,
$\gamma = \left (\begin {matrix} a & b \\ c & d \end {matrix}\right ) \in \varGamma :=\mathrm {SL}_2(\mathbb {Z})$
,
![]() $c>0$
, we have [Reference Apostol4, Theorem 3.4]
$c>0$
, we have [Reference Apostol4, Theorem 3.4]
where
![]() $s(d,c)$
is the Dedekind sum given by
$s(d,c)$
is the Dedekind sum given by
 $$ \begin{align*} s(d,c) := \sum_{n=0}^{c-1} \frac{n}{c} \left(\frac{dn}{c}-\left\lfloor \frac{dn}{c} \right\rfloor-\frac{1}{2} \right). \end{align*} $$
$$ \begin{align*} s(d,c) := \sum_{n=0}^{c-1} \frac{n}{c} \left(\frac{dn}{c}-\left\lfloor \frac{dn}{c} \right\rfloor-\frac{1}{2} \right). \end{align*} $$
Set
 $$ \begin{align*} F(e^{2\pi i \tau}) := \frac{1}{(q;q)_{\infty}} = \frac{e^{\pi i \tau/12}}{\eta(\tau)}. \end{align*} $$
$$ \begin{align*} F(e^{2\pi i \tau}) := \frac{1}{(q;q)_{\infty}} = \frac{e^{\pi i \tau/12}}{\eta(\tau)}. \end{align*} $$
It follows from (2.2) that
For the interval
![]() $\xi _{h,k},$
if
$\xi _{h,k},$
if
![]() $\mathrm {gcd}(n,k)=1$
, then we choose an integer
$\mathrm {gcd}(n,k)=1$
, then we choose an integer
![]() $h_n^{\prime }$
such that
$h_n^{\prime }$
such that
![]() $nhh_n^{\prime } \equiv -1 ~ (\mathrm {mod} ~ k).$
Hence, there exists
$nhh_n^{\prime } \equiv -1 ~ (\mathrm {mod} ~ k).$
Hence, there exists
![]() $b_n\in \mathbb {Z}$
such that
$b_n\in \mathbb {Z}$
such that
![]() $nhh_n^{\prime } - b_n k = -1.$
Set
$nhh_n^{\prime } - b_n k = -1.$
Set
 $$ \begin{align*} \gamma_{(nh,k)} := \left(\begin{matrix} h_n^{\prime} & -b_n \\ k & -nh \end{matrix} \right) \in \varGamma. \end{align*} $$
$$ \begin{align*} \gamma_{(nh,k)} := \left(\begin{matrix} h_n^{\prime} & -b_n \\ k & -nh \end{matrix} \right) \in \varGamma. \end{align*} $$
Then,
 $$ \begin{align*} \begin{aligned} \gamma_{(nh,k)} = \frac{h_n^{\prime} \frac{nh+inz}{k}-b_n}{k \frac{nh+inz}{k}-nh} = \frac{h_n^{\prime} nh - b_n k + in h_n^{\prime} z}{k i nz} = \frac{h_n^{\prime}}{k} + i\frac{1}{knz}, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \gamma_{(nh,k)} = \frac{h_n^{\prime} \frac{nh+inz}{k}-b_n}{k \frac{nh+inz}{k}-nh} = \frac{h_n^{\prime} nh - b_n k + in h_n^{\prime} z}{k i nz} = \frac{h_n^{\prime}}{k} + i\frac{1}{knz}, \end{aligned} \end{align*} $$
so that
and
2.3 Some bounds and an integral
It is obvious to observe that
From this, we have
and
Notice that
![]() $z=k(\varrho - i \varphi ).$
Then,
$z=k(\varrho - i \varphi ).$
Then,
 $$ \begin{align} \mathrm{Re}\left(\frac{1}{z}\right) = \mathrm{Re}\left(\frac{1}{k(\varrho - i \varphi)}\right) = \frac{1}{k}\frac{\varrho}{\varrho^2 + \varphi^2} \geq \frac{1}{k}\frac{N^{-2}}{N^{-4} + k^{-2}N^{-2}} \geq \frac{k}{2}. \end{align} $$
$$ \begin{align} \mathrm{Re}\left(\frac{1}{z}\right) = \mathrm{Re}\left(\frac{1}{k(\varrho - i \varphi)}\right) = \frac{1}{k}\frac{\varrho}{\varrho^2 + \varphi^2} \geq \frac{1}{k}\frac{N^{-2}}{N^{-4} + k^{-2}N^{-2}} \geq \frac{k}{2}. \end{align} $$
Also, we have
We now estimate the function
![]() $\mathrm {log}F(x)$
for
$\mathrm {log}F(x)$
for
![]() $0 < x < 1.$
Since
$0 < x < 1.$
Since
![]() $0 < x <1$
, we have
$0 < x <1$
, we have
From this, we deduce that
so that
Then
 $$ \begin{align} \begin{aligned} \mathrm{log}F(x) &= \sum_{n=1}^{\infty} - \mathrm{log}(1-x^n) = \sum_{n=1}^{\infty} \sum_{m=1}^{\infty} \frac{x^{nm}}{m} = \sum_{m=1}^{\infty} \frac{x^m}{m(1-x^m)}\\ &\leq \frac{x}{1-x} \sum_{m=1}^{\infty} \frac{1}{m^2} = \frac{\pi^2}{6} \frac{x}{1-x}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \mathrm{log}F(x) &= \sum_{n=1}^{\infty} - \mathrm{log}(1-x^n) = \sum_{n=1}^{\infty} \sum_{m=1}^{\infty} \frac{x^{nm}}{m} = \sum_{m=1}^{\infty} \frac{x^m}{m(1-x^m)}\\ &\leq \frac{x}{1-x} \sum_{m=1}^{\infty} \frac{1}{m^2} = \frac{\pi^2}{6} \frac{x}{1-x}. \end{aligned} \end{align} $$
Let
![]() $q_m(n)$
denote the number of m-colored partitions of n into an even number of distinct parts minus the number of m-colored partitions of n into an odd number of distinct parts. Then, by [Reference Andrews and Berndt2, eq.(6.1.3)]
$q_m(n)$
denote the number of m-colored partitions of n into an even number of distinct parts minus the number of m-colored partitions of n into an odd number of distinct parts. Then, by [Reference Andrews and Berndt2, eq.(6.1.3)]
Define
![]() $\hat {a}_1(n)$
(resp.
$\hat {a}_1(n)$
(resp.
![]() $\hat {a}_2(n)$
) as the number of partitions of n into an even (resp. odd) number of parts with distinct elements. Then, we have
$\hat {a}_2(n)$
) as the number of partitions of n into an even (resp. odd) number of parts with distinct elements. Then, we have
![]() $q_1(n) = \hat {a}_1(n) - \hat {a}_2(n).$
Since
$q_1(n) = \hat {a}_1(n) - \hat {a}_2(n).$
Since
![]() $0 \leq \hat {a}_1(n) \leq p(n)$
,
$0 \leq \hat {a}_1(n) \leq p(n)$
,
![]() $0 \leq \hat {a}_2(n) \leq p(n)$
, we have
$0 \leq \hat {a}_2(n) \leq p(n)$
, we have
Then,
 $$ \begin{align} \begin{aligned} \left| \frac{1}{F(e^{2\pi i \tau})} \right| &\leq \sum_{n=1}^{\infty} |q_1(n)| |e^{2\pi i n \tau}| \leq \sum_{n=1}^{\infty} p(n) |e^{2\pi i n \tau}| \\ &=F(|e^{2\pi i \tau}|) = F(e^{-2\pi \mathrm{Im}(\tau)})\\ & \leq \mathrm{exp} \left(\frac{\pi^2 e^{-2\pi \mathrm{Im}(\tau)}}{6(1-e^{-2\pi \mathrm{Im}(\tau)})}\right), \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \left| \frac{1}{F(e^{2\pi i \tau})} \right| &\leq \sum_{n=1}^{\infty} |q_1(n)| |e^{2\pi i n \tau}| \leq \sum_{n=1}^{\infty} p(n) |e^{2\pi i n \tau}| \\ &=F(|e^{2\pi i \tau}|) = F(e^{-2\pi \mathrm{Im}(\tau)})\\ & \leq \mathrm{exp} \left(\frac{\pi^2 e^{-2\pi \mathrm{Im}(\tau)}}{6(1-e^{-2\pi \mathrm{Im}(\tau)})}\right), \end{aligned} \end{align} $$
where the last inequality follows from (2.7).
An inequality for
![]() $F(e^{2\pi i \tau })$
is given in the following lemma.
$F(e^{2\pi i \tau })$
is given in the following lemma.
Lemma 2.1 Let
![]() $\tau _1,\tau _2,\cdots ,\tau _n \in \mathbb {C}$
and let
$\tau _1,\tau _2,\cdots ,\tau _n \in \mathbb {C}$
and let
![]() $m_1,m_2,\cdots ,m_n \in \mathbb {Z}\backslash \{0\}.$
Then,
$m_1,m_2,\cdots ,m_n \in \mathbb {Z}\backslash \{0\}.$
Then,
 $$ \begin{align} \left|\prod_{i=1}^{n} F(e^{2\pi i \tau_i})^{m_i} - 1\right| \leq \mathrm{exp}\left(\sum_{i=1}^{n} \frac{|m_i| \pi^2 e^{-2\pi \mathrm{Im}(\tau_i)}}{6(1-e^{-2\pi \mathrm{Im}(\tau_i)})} \right) - 1. \end{align} $$
$$ \begin{align} \left|\prod_{i=1}^{n} F(e^{2\pi i \tau_i})^{m_i} - 1\right| \leq \mathrm{exp}\left(\sum_{i=1}^{n} \frac{|m_i| \pi^2 e^{-2\pi \mathrm{Im}(\tau_i)}}{6(1-e^{-2\pi \mathrm{Im}(\tau_i)})} \right) - 1. \end{align} $$
Proof Let
If
![]() $m_i \geq 0$
, then
$m_i \geq 0$
, then
![]() $|c_i(n)| = \tilde {c}_i(n);$
if
$|c_i(n)| = \tilde {c}_i(n);$
if
![]() $m_i < 0$
, then, by (2.8),
$m_i < 0$
, then, by (2.8),
 $$ \begin{align*} |c_i(n)| \leq \sum_{\substack{1 \leq j \leq |m_i| \\ \sum n_j= n}} |q_1(n_j)| \leq \sum_{\substack{1 \leq j \leq |m_i| \\ \sum n_j = n}} p(n_j) = \tilde{c}_i(n). \end{align*} $$
$$ \begin{align*} |c_i(n)| \leq \sum_{\substack{1 \leq j \leq |m_i| \\ \sum n_j= n}} |q_1(n_j)| \leq \sum_{\substack{1 \leq j \leq |m_i| \\ \sum n_j = n}} p(n_j) = \tilde{c}_i(n). \end{align*} $$
Hence, by (2.7),
 $$ \begin{align*} \begin{aligned} \left|\prod_{i=1}^{n} F(e^{2\pi i \tau_i})^{m_i} - 1\right| &\leq \left|\sum_{k_1=0}^{\infty}\cdots \sum_{k_n=0}^{\infty}c_1(k_1)\cdots c_n(k_n)e^{2\pi i k_1 \tau_1}\cdots e^{2\pi i k_n \tau_n} - 1\right|\\ & \leq \mathop{\sum_{k_1=0}^{\infty} \cdots\sum_{k_n=0}^{\infty}}\limits_{(k_1,\cdots,k_n)\neq (0,\cdots,0)} \tilde{c}_1(k_1)\cdots \tilde{c}_n(k_n)|e^{2\pi i k_1 \tau_1}|\cdots |e^{2\pi i k_n \tau_n}|\\&= \prod_{i=1}^{n} F(|e^{2\pi i \tau_i}|)^{|m_i|} - 1\\ &\leq \mathrm{exp}\left(\sum_{i=1}^{n} \frac{|m_i| \pi^2 e^{-2\pi \mathrm{Im}(\tau_i)}}{6(1-e^{-2\pi \mathrm{Im}(\tau_i)})} \right) - 1. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \left|\prod_{i=1}^{n} F(e^{2\pi i \tau_i})^{m_i} - 1\right| &\leq \left|\sum_{k_1=0}^{\infty}\cdots \sum_{k_n=0}^{\infty}c_1(k_1)\cdots c_n(k_n)e^{2\pi i k_1 \tau_1}\cdots e^{2\pi i k_n \tau_n} - 1\right|\\ & \leq \mathop{\sum_{k_1=0}^{\infty} \cdots\sum_{k_n=0}^{\infty}}\limits_{(k_1,\cdots,k_n)\neq (0,\cdots,0)} \tilde{c}_1(k_1)\cdots \tilde{c}_n(k_n)|e^{2\pi i k_1 \tau_1}|\cdots |e^{2\pi i k_n \tau_n}|\\&= \prod_{i=1}^{n} F(|e^{2\pi i \tau_i}|)^{|m_i|} - 1\\ &\leq \mathrm{exp}\left(\sum_{i=1}^{n} \frac{|m_i| \pi^2 e^{-2\pi \mathrm{Im}(\tau_i)}}{6(1-e^{-2\pi \mathrm{Im}(\tau_i)})} \right) - 1. \end{aligned} \end{align*} $$
This completes the proof.
To facilitate certain bounds in the proof of Theorem 1.1, we examine monotonicity of a function here.
Lemma 2.2 Let
![]() $u_1,u_2,\cdots ,u_n \in \mathbb {R}_{\geq 1}$
and let
$u_1,u_2,\cdots ,u_n \in \mathbb {R}_{\geq 1}$
and let
![]() $m_1,m_2,\cdots ,m_n \in \mathbb {N}.$
Then,
$m_1,m_2,\cdots ,m_n \in \mathbb {N}.$
Then,
 $$ \begin{align*} W(x) := \frac{1}{x}\left(\mathrm{exp}\left(\sum_{i=1}^{n} \frac{m_i \pi^2 x^{u_i}}{6(1-x^{u_i})}\right) - 1\right) \end{align*} $$
$$ \begin{align*} W(x) := \frac{1}{x}\left(\mathrm{exp}\left(\sum_{i=1}^{n} \frac{m_i \pi^2 x^{u_i}}{6(1-x^{u_i})}\right) - 1\right) \end{align*} $$
is a nondecreasing function of x on
![]() $(0,1)$
.
$(0,1)$
.
Proof Taking derivative of
![]() $W(x)$
yields
$W(x)$
yields
 $$ \begin{align*} \begin{aligned} W^{\prime}(x) = & -\frac{1}{x^2}\left(\mathrm{exp}\left(\sum_{i=1}^{n} \frac{m_i \pi^2 x^{u_i}}{6(1-x^{u_i})}\right) - 1\right) \\ & + \frac{1}{x}\mathrm{exp}\left(\sum_{i=1}^{n} \frac{m_i \pi^2 x^{u_i}}{6(1-x^{u_i})}\right) \sum_{i=1}^{n}\frac{\pi^2 m_i}{6} \left(\frac{u_ix^{u_i-1}}{(1-x^{u_i})^2}\right). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} W^{\prime}(x) = & -\frac{1}{x^2}\left(\mathrm{exp}\left(\sum_{i=1}^{n} \frac{m_i \pi^2 x^{u_i}}{6(1-x^{u_i})}\right) - 1\right) \\ & + \frac{1}{x}\mathrm{exp}\left(\sum_{i=1}^{n} \frac{m_i \pi^2 x^{u_i}}{6(1-x^{u_i})}\right) \sum_{i=1}^{n}\frac{\pi^2 m_i}{6} \left(\frac{u_ix^{u_i-1}}{(1-x^{u_i})^2}\right). \end{aligned} \end{align*} $$
Therefore, it suffices to prove
 $$ \begin{align} \sum_{i=1}^{n}\frac{\pi^2 m_i}{6} \left(\frac{u_ix^{u_i}}{(1-x^{u_i})^2}\right) + \mathrm{exp}\left(-\sum_{i=1}^{n} \frac{\pi^2 m_i}{6}\frac{x^{u_i}}{1-x^{u_i}}\right) \geq 1 \end{align} $$
$$ \begin{align} \sum_{i=1}^{n}\frac{\pi^2 m_i}{6} \left(\frac{u_ix^{u_i}}{(1-x^{u_i})^2}\right) + \mathrm{exp}\left(-\sum_{i=1}^{n} \frac{\pi^2 m_i}{6}\frac{x^{u_i}}{1-x^{u_i}}\right) \geq 1 \end{align} $$
for
![]() $x \in (0,1)$
. Since
$x \in (0,1)$
. Since
 $$ \begin{align*} \frac{u_ix^{u_i}}{(1-x^{u_i})^2} - \frac{x^{u_i}}{1-x^{u_i}} = \frac{(u_i-1) x^{u_i} + x^{2u_i}}{(1-x^{u_i})^2}\geq 0 \end{align*} $$
$$ \begin{align*} \frac{u_ix^{u_i}}{(1-x^{u_i})^2} - \frac{x^{u_i}}{1-x^{u_i}} = \frac{(u_i-1) x^{u_i} + x^{2u_i}}{(1-x^{u_i})^2}\geq 0 \end{align*} $$
for
![]() $u_i \geq 1$
, we have
$u_i \geq 1$
, we have
 $$ \begin{align} \begin{aligned} & \sum_{i=1}^{n}\frac{\pi^2 m_i}{6} \left(\frac{u_ix^{u_i}}{(1-x^{u_i})^2}\right) + \mathrm{exp}\left(-\sum_{i=1}^{n} \frac{\pi^2 m_i}{6}\frac{x^{u_i}}{1-x^{u_i}}\right) \\ &\qquad \geq \sum_{i=1}^{n} \frac{\pi^2 m_i}{6}\frac{x^{u_i}}{1-x^{u_i}}+ \mathrm{exp}\left(-\sum_{i=1}^{n} \frac{\pi^2 m_i}{6}\frac{x^{u_i}}{1-x^{u_i}}\right). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} & \sum_{i=1}^{n}\frac{\pi^2 m_i}{6} \left(\frac{u_ix^{u_i}}{(1-x^{u_i})^2}\right) + \mathrm{exp}\left(-\sum_{i=1}^{n} \frac{\pi^2 m_i}{6}\frac{x^{u_i}}{1-x^{u_i}}\right) \\ &\qquad \geq \sum_{i=1}^{n} \frac{\pi^2 m_i}{6}\frac{x^{u_i}}{1-x^{u_i}}+ \mathrm{exp}\left(-\sum_{i=1}^{n} \frac{\pi^2 m_i}{6}\frac{x^{u_i}}{1-x^{u_i}}\right). \end{aligned} \end{align} $$
Let
 $$ \begin{align*} y := \sum_{i=1}^{n} \frac{\pi^2 m_i}{6}\frac{x^{u_i}}{1-x^{u_i}}. \end{align*} $$
$$ \begin{align*} y := \sum_{i=1}^{n} \frac{\pi^2 m_i}{6}\frac{x^{u_i}}{1-x^{u_i}}. \end{align*} $$
Then,
![]() $y>0$
, and so
$y>0$
, and so
![]() $y + e^{-y} \geq 1.$
From this and (2.12), we easily obtain the inequality (2.11).
$y + e^{-y} \geq 1.$
From this and (2.12), we easily obtain the inequality (2.11).
An estimate for a useful integral is given in the following form. Even though it contains the result in [Reference Chan9, Lemma 3.2] as a special case, its proof is similar to that of [Reference Chan9, Lemma 3.2], and we omit it here.
Lemma 2.3 Let
![]() $(h,k)=1$
,
$(h,k)=1$
,
![]() $b \in \mathbb {R}_{\geq 0}$
, and define
$b \in \mathbb {R}_{\geq 0}$
, and define
Then,
 $$ \begin{align*} I = \sqrt{\frac{2}{k(n-1/24)}} b^{1/4} \mathrm{cosh}\left(\frac{\pi}{k} \sqrt{\frac{2b}{3}\left(n-\frac{1}{24}\right)} \right) + E^{(b)}(I), \end{align*} $$
$$ \begin{align*} I = \sqrt{\frac{2}{k(n-1/24)}} b^{1/4} \mathrm{cosh}\left(\frac{\pi}{k} \sqrt{\frac{2b}{3}\left(n-\frac{1}{24}\right)} \right) + E^{(b)}(I), \end{align*} $$
where
 $$ \begin{align*} |E^{(b)}(I)| \leq \sqrt{2} \pi^{-1} e^{b \pi / 3 } \frac{e^{2\pi (n-1/24) \varrho} N^{1/2}}{n-1/24}. \end{align*} $$
$$ \begin{align*} |E^{(b)}(I)| \leq \sqrt{2} \pi^{-1} e^{b \pi / 3 } \frac{e^{2\pi (n-1/24) \varrho} N^{1/2}}{n-1/24}. \end{align*} $$
The following inequalities are also important in the proof of Theorem 1.1.
 $$ \begin{align*} \sum_{k=1}^{N} k^n \leq \begin{cases} N^{n+1}, & \mathrm{if} ~ n\geq0, \\ \frac{1}{n+1} N^{n+1}, & \mathrm{if} ~ -1 < n<0. \end{cases} \end{align*} $$
$$ \begin{align*} \sum_{k=1}^{N} k^n \leq \begin{cases} N^{n+1}, & \mathrm{if} ~ n\geq0, \\ \frac{1}{n+1} N^{n+1}, & \mathrm{if} ~ -1 < n<0. \end{cases} \end{align*} $$
3 Proof of Theorem 1.1
Let
 $$ \begin{align} \sum_{n=0}^{\infty} a(n) q^n := \frac{(q^9;q^9)_{\infty}^{3}}{(q;q)_{\infty}(q^{27};q^{27})_{\infty}} = \frac{F(e^{2\pi i \tau})F(e^{2\pi i (27\tau)})}{F(e^{2\pi i (9\tau)})^3}=: g(q) \end{align} $$
$$ \begin{align} \sum_{n=0}^{\infty} a(n) q^n := \frac{(q^9;q^9)_{\infty}^{3}}{(q;q)_{\infty}(q^{27};q^{27})_{\infty}} = \frac{F(e^{2\pi i \tau})F(e^{2\pi i (27\tau)})}{F(e^{2\pi i (9\tau)})^3}=: g(q) \end{align} $$
and
 $$ \begin{align} \begin{aligned}\sum_{n=0}^{\infty} b(n) q^n &:= q^2 \frac{(q^3;q^3)_{\infty}(q^{27};q^{27})_{\infty}^2}{(q;q)_{\infty}(q^9;q^9)_{\infty}}\\ &= e^{2\pi i (2\tau)} \frac{F(e^{2\pi i \tau})F(e^{2\pi i (9\tau)})}{F(e^{2\pi i (3\tau)})F(e^{2\pi i (27\tau)})^2}=: h(q) \end{aligned}\end{align} $$
$$ \begin{align} \begin{aligned}\sum_{n=0}^{\infty} b(n) q^n &:= q^2 \frac{(q^3;q^3)_{\infty}(q^{27};q^{27})_{\infty}^2}{(q;q)_{\infty}(q^9;q^9)_{\infty}}\\ &= e^{2\pi i (2\tau)} \frac{F(e^{2\pi i \tau})F(e^{2\pi i (9\tau)})}{F(e^{2\pi i (3\tau)})F(e^{2\pi i (27\tau)})^2}=: h(q) \end{aligned}\end{align} $$
with
![]() $q=e^{2\pi i \tau }.$
$q=e^{2\pi i \tau }.$
In this section, we first employ the modification [Reference Kane14] of the circle method to estimate the coefficient
![]() $a(n)$
of
$a(n)$
of
![]() $g(q)$
and the coefficient
$g(q)$
and the coefficient
![]() $b(n)$
of
$b(n)$
of
![]() $h(q)$
and then obtain information about the sign of the coefficients
$h(q)$
and then obtain information about the sign of the coefficients
![]() $\{a(n) - 3b(n)\}_{n \geq 0}$
of
$\{a(n) - 3b(n)\}_{n \geq 0}$
of
![]() $g(q)-3h(q).$
Finally, by [Reference Aygin and Chan6, eqs.(2.10) and (2.11)], we know that
$g(q)-3h(q).$
Finally, by [Reference Aygin and Chan6, eqs.(2.10) and (2.11)], we know that
 $$ \begin{align*} \begin{aligned} M(0,1,1;9;n) - \frac{p(n)}{3} &= \frac{2}{3}(a(n) - 3b(n) ), \\ M(2,3,4;9;n) - \frac{p(n)}{3} &= -\frac{1}{3}(a(n) - 3b(n) ). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} M(0,1,1;9;n) - \frac{p(n)}{3} &= \frac{2}{3}(a(n) - 3b(n) ), \\ M(2,3,4;9;n) - \frac{p(n)}{3} &= -\frac{1}{3}(a(n) - 3b(n) ). \end{aligned} \end{align*} $$
Therefore, from the sign information of the coefficients
![]() $\{a(n) - 3b(n)\}_{n \geq 0}$
, we can deduce the inequalities in Theorem 1.1.
$\{a(n) - 3b(n)\}_{n \geq 0}$
, we can deduce the inequalities in Theorem 1.1.
Since
![]() $\mathrm {gcd}(k,27)=1,3,9$
or
$\mathrm {gcd}(k,27)=1,3,9$
or
![]() $27,$
we split each of the sums
$27,$
we split each of the sums
![]() $\sum _{\substack {0 \leq h<k \leq N \\ (h,k) = 1}}$
for
$\sum _{\substack {0 \leq h<k \leq N \\ (h,k) = 1}}$
for
![]() $a(n)$
and
$a(n)$
and
![]() $b(n)$
into four parts according to the values of
$b(n)$
into four parts according to the values of
![]() $\mathrm {gcd}(k,27).$
$\mathrm {gcd}(k,27).$
It follows from (2.1) that
 $$ \begin{align} \begin{aligned} a(n)&= \sum_{\substack{0 \leq h<k \leq N \\ (h,k) = 1}} e^{-2\pi i nh/k} \int_{\xi_{h,k}} \frac{F(e^{2\pi i \tau})F(e^{2\pi i (27\tau)})}{F(e^{2\pi i (9\tau)})^3} e^{2\pi n \varrho} e^{-2\pi i n \varphi} d\varphi \\ &=\bigg(\sum_{\substack{1 \leq k \leq N \\ (k,27) = 1}} + \sum_{\substack{1 \leq k \leq N \\ (k,27) = 3}} + \sum_{\substack{1 \leq k \leq N \\ (k,27) = 9}} + \sum_{\substack{1 \leq k \leq N \\ (k,27) = 27}}\bigg) \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} e^{-2\pi i nh/k} \\ & \;\;\times \int_{\xi_{h,k}} \frac{F(e^{2\pi i \tau})F(e^{2\pi i (27\tau)})}{F(e^{2\pi i (9\tau)})^3} e^{2\pi n \varrho} e^{-2\pi i n \varphi} d\varphi \\ &=: S_1(A) + S_2(A) + S_3(A) + S_4(A) \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} a(n)&= \sum_{\substack{0 \leq h<k \leq N \\ (h,k) = 1}} e^{-2\pi i nh/k} \int_{\xi_{h,k}} \frac{F(e^{2\pi i \tau})F(e^{2\pi i (27\tau)})}{F(e^{2\pi i (9\tau)})^3} e^{2\pi n \varrho} e^{-2\pi i n \varphi} d\varphi \\ &=\bigg(\sum_{\substack{1 \leq k \leq N \\ (k,27) = 1}} + \sum_{\substack{1 \leq k \leq N \\ (k,27) = 3}} + \sum_{\substack{1 \leq k \leq N \\ (k,27) = 9}} + \sum_{\substack{1 \leq k \leq N \\ (k,27) = 27}}\bigg) \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} e^{-2\pi i nh/k} \\ & \;\;\times \int_{\xi_{h,k}} \frac{F(e^{2\pi i \tau})F(e^{2\pi i (27\tau)})}{F(e^{2\pi i (9\tau)})^3} e^{2\pi n \varrho} e^{-2\pi i n \varphi} d\varphi \\ &=: S_1(A) + S_2(A) + S_3(A) + S_4(A) \end{aligned} \end{align} $$
with
 $$ \begin{align*} A = \frac{F(e^{2\pi i \tau})F(e^{2\pi i (27\tau)})}{F(e^{2\pi i (9\tau)})^3} e^{2\pi n \varrho} e^{-2\pi i n \varphi} \end{align*} $$
$$ \begin{align*} A = \frac{F(e^{2\pi i \tau})F(e^{2\pi i (27\tau)})}{F(e^{2\pi i (9\tau)})^3} e^{2\pi n \varrho} e^{-2\pi i n \varphi} \end{align*} $$
and
Similarly, we get
 $$ \begin{align} \begin{aligned} b(n)&=\sum_{\substack{0 \leq h<k \leq N \\ (h,k) = 1}} e^{-2\pi i nh/k} \int_{\xi_{h,k}} e^{2\pi i (2\tau)} \frac{F(e^{2\pi i \tau})F(e^{2\pi i (9\tau)})}{F(e^{2\pi i (3\tau)})F(e^{2\pi i (27\tau)})^2} e^{2\pi n \varrho} e^{-2\pi i n \varphi} d\varphi \\ &=\bigg (\sum_{\substack{1 \leq k \leq N \\ (k,27) = 1}} + \sum_{\substack{1 \leq k \leq N \\ (k,27) = 3}} + \sum_{\substack{1 \leq k \leq N \\ (k,27) = 9}} + \sum_{\substack{1 \leq k \leq N \\ (k,27) = 27}}\bigg) \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} e^{-2\pi i nh/k} \\ &\;\;\times \int_{\xi_{h,k}} e^{2\pi i (2\tau)} \frac{F(e^{2\pi i \tau})F(e^{2\pi i (9\tau)})}{F(e^{2\pi i (3\tau)})F(e^{2\pi i (27\tau)})^2} e^{2\pi n \varrho} e^{-2\pi i n \varphi} d\varphi \\ &=: S_1(B) + S_2(B) + S_3(B) + S_4(B) \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} b(n)&=\sum_{\substack{0 \leq h<k \leq N \\ (h,k) = 1}} e^{-2\pi i nh/k} \int_{\xi_{h,k}} e^{2\pi i (2\tau)} \frac{F(e^{2\pi i \tau})F(e^{2\pi i (9\tau)})}{F(e^{2\pi i (3\tau)})F(e^{2\pi i (27\tau)})^2} e^{2\pi n \varrho} e^{-2\pi i n \varphi} d\varphi \\ &=\bigg (\sum_{\substack{1 \leq k \leq N \\ (k,27) = 1}} + \sum_{\substack{1 \leq k \leq N \\ (k,27) = 3}} + \sum_{\substack{1 \leq k \leq N \\ (k,27) = 9}} + \sum_{\substack{1 \leq k \leq N \\ (k,27) = 27}}\bigg) \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} e^{-2\pi i nh/k} \\ &\;\;\times \int_{\xi_{h,k}} e^{2\pi i (2\tau)} \frac{F(e^{2\pi i \tau})F(e^{2\pi i (9\tau)})}{F(e^{2\pi i (3\tau)})F(e^{2\pi i (27\tau)})^2} e^{2\pi n \varrho} e^{-2\pi i n \varphi} d\varphi \\ &=: S_1(B) + S_2(B) + S_3(B) + S_4(B) \end{aligned} \end{align} $$
with
 $$ \begin{align*} B = e^{2\pi i (2\tau)} \frac{F(e^{2\pi i \tau})F(e^{2\pi i (9\tau)})}{F(e^{2\pi i (3\tau)})F(e^{2\pi i (27\tau)})^2} e^{2\pi n \varrho} e^{-2\pi i n \varphi}. \end{align*} $$
$$ \begin{align*} B = e^{2\pi i (2\tau)} \frac{F(e^{2\pi i \tau})F(e^{2\pi i (9\tau)})}{F(e^{2\pi i (3\tau)})F(e^{2\pi i (27\tau)})^2} e^{2\pi n \varrho} e^{-2\pi i n \varphi}. \end{align*} $$
3.1 Transformation formulas for g and h
We apply (2.4) to transform g and h according to the values of
![]() $\mathrm {gcd}(k,27).$
$\mathrm {gcd}(k,27).$
Case 1:
![]() $\mathrm {gcd}(k,27)=1$
. By (2.4), we have
$\mathrm {gcd}(k,27)=1$
. By (2.4), we have
 $$ \begin{align} \begin{aligned} \frac{F(e^{2\pi i \tau})F(e^{2\pi i (27\tau)})}{F(e^{2\pi i (9\tau)})^3}\ &= \frac{1}{3 \sqrt{3} \sqrt{z}} \frac{F(e^{2\pi i \gamma_{(h,k)} (\tau)})F(e^{2\pi i \gamma_{(27h,k)} (27\tau)})}{F(e^{2\pi i \gamma_{(9h,k)} (9\tau)})^3} \\ &\quad\times e^{\pi i (s(h,k) + s(27h,k) - 3s(9h,k))} e^{\frac{\pi}{12k}(\frac{19}{27z} - z)} \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \frac{F(e^{2\pi i \tau})F(e^{2\pi i (27\tau)})}{F(e^{2\pi i (9\tau)})^3}\ &= \frac{1}{3 \sqrt{3} \sqrt{z}} \frac{F(e^{2\pi i \gamma_{(h,k)} (\tau)})F(e^{2\pi i \gamma_{(27h,k)} (27\tau)})}{F(e^{2\pi i \gamma_{(9h,k)} (9\tau)})^3} \\ &\quad\times e^{\pi i (s(h,k) + s(27h,k) - 3s(9h,k))} e^{\frac{\pi}{12k}(\frac{19}{27z} - z)} \end{aligned} \end{align} $$
and
 $$ \begin{align} \begin{aligned} &e^{2\pi i (2\tau)} \frac{F(e^{2\pi i \tau})F(e^{2\pi i (9\tau)})}{F(e^{2\pi i (3\tau)})F(e^{2\pi i (27\tau)})^2}\\ &\quad= \frac{1}{9 \sqrt{3} \sqrt{z}} \frac{F(e^{2\pi i \gamma_{(h,k)} (\tau)})F(e^{2\pi i \gamma_{(9h,k)} (9\tau)})}{F(e^{2\pi i \gamma_{(3h,k)} (3\tau)})F(e^{2\pi i \gamma_{(27h,k)} (27\tau)})^2} \\ &\qquad\times e^{2\pi i (2h/k)} e^{\pi \frac{-48z}{12k}}e^{\pi i (s(h,k) + s(9h,k) - s(3h,k) - 2s(27h,k))} e^{\frac{\pi}{12k}(\frac{19}{27z} + 47z)} \\ &\quad= \frac{1}{9 \sqrt{3} \sqrt{z}} \frac{F(e^{2\pi i \gamma_{(h,k)} (\tau)})F(e^{2\pi i \gamma_{(9h,k)} (9\tau)})}{F(e^{2\pi i \gamma_{(3h,k)} (3\tau)})F(e^{2\pi i \gamma_{(27h,k)} (27\tau)})^2} \\ &\qquad \times e^{2\pi i (2h/k)} e^{\pi i (s(h,k) + s(9h,k) - s(3h,k)) - 2s(27h,k)} e^{\frac{\pi}{12k}(\frac{19}{27z} - z)}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &e^{2\pi i (2\tau)} \frac{F(e^{2\pi i \tau})F(e^{2\pi i (9\tau)})}{F(e^{2\pi i (3\tau)})F(e^{2\pi i (27\tau)})^2}\\ &\quad= \frac{1}{9 \sqrt{3} \sqrt{z}} \frac{F(e^{2\pi i \gamma_{(h,k)} (\tau)})F(e^{2\pi i \gamma_{(9h,k)} (9\tau)})}{F(e^{2\pi i \gamma_{(3h,k)} (3\tau)})F(e^{2\pi i \gamma_{(27h,k)} (27\tau)})^2} \\ &\qquad\times e^{2\pi i (2h/k)} e^{\pi \frac{-48z}{12k}}e^{\pi i (s(h,k) + s(9h,k) - s(3h,k) - 2s(27h,k))} e^{\frac{\pi}{12k}(\frac{19}{27z} + 47z)} \\ &\quad= \frac{1}{9 \sqrt{3} \sqrt{z}} \frac{F(e^{2\pi i \gamma_{(h,k)} (\tau)})F(e^{2\pi i \gamma_{(9h,k)} (9\tau)})}{F(e^{2\pi i \gamma_{(3h,k)} (3\tau)})F(e^{2\pi i \gamma_{(27h,k)} (27\tau)})^2} \\ &\qquad \times e^{2\pi i (2h/k)} e^{\pi i (s(h,k) + s(9h,k) - s(3h,k)) - 2s(27h,k)} e^{\frac{\pi}{12k}(\frac{19}{27z} - z)}. \end{aligned} \end{align} $$
Case 2:
![]() $\mathrm {gcd}(k,27)=3$
. Let
$\mathrm {gcd}(k,27)=3$
. Let
![]() $k = 3l_1.$
Then,
$k = 3l_1.$
Then,
 $$ \begin{align} \begin{aligned} \frac{F(e^{2\pi i \tau})F(e^{2\pi i (27\tau)})}{F(e^{2\pi i (9\tau)})^3} &= \frac{1}{\sqrt{3} \sqrt{z}} \frac{F(e^{2\pi i \gamma_{(h,3l_1)} (\tau)})F(e^{2\pi i \gamma_{(9h,l_1)} (27\tau)})}{F(e^{2\pi i \gamma_{(3h,l_1)} (9\tau)})^3}\\ &\quad \times e^{\pi i (s(h,3l_1) + s(9h,l_1) - 3s(3h,l_1))} e^{\frac{\pi}{12k}(-\frac{5}{3z} - z)} \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \frac{F(e^{2\pi i \tau})F(e^{2\pi i (27\tau)})}{F(e^{2\pi i (9\tau)})^3} &= \frac{1}{\sqrt{3} \sqrt{z}} \frac{F(e^{2\pi i \gamma_{(h,3l_1)} (\tau)})F(e^{2\pi i \gamma_{(9h,l_1)} (27\tau)})}{F(e^{2\pi i \gamma_{(3h,l_1)} (9\tau)})^3}\\ &\quad \times e^{\pi i (s(h,3l_1) + s(9h,l_1) - 3s(3h,l_1))} e^{\frac{\pi}{12k}(-\frac{5}{3z} - z)} \end{aligned} \end{align} $$
and
 $$ \begin{align} \begin{aligned} &e^{2\pi i (2\tau)} \frac{F(e^{2\pi i \tau})F(e^{2\pi i (9\tau)})}{F(e^{2\pi i (3\tau)})F(e^{2\pi i (27\tau)})^2}\\ &\quad=\frac{1}{3 \sqrt{3} \sqrt{z}} \frac{F(e^{2\pi i \gamma_{(h,3l_1)} (\tau)})F(e^{2\pi i \gamma_{(3h,l_1)} (9\tau)})}{F(e^{2\pi i \gamma_{(h,l_1)} (3\tau)})F(e^{2\pi i \gamma_{(9h,l_1)} (27\tau)})^2}\\ & \qquad \times e^{2\pi i (2h/k)} e^{\pi i (s(h,3l_1) + s(3h,l_1) - s(h,l_1) - 2s(9h,l_1))} e^{\frac{\pi}{12k}(-\frac{5}{3z} - z)}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &e^{2\pi i (2\tau)} \frac{F(e^{2\pi i \tau})F(e^{2\pi i (9\tau)})}{F(e^{2\pi i (3\tau)})F(e^{2\pi i (27\tau)})^2}\\ &\quad=\frac{1}{3 \sqrt{3} \sqrt{z}} \frac{F(e^{2\pi i \gamma_{(h,3l_1)} (\tau)})F(e^{2\pi i \gamma_{(3h,l_1)} (9\tau)})}{F(e^{2\pi i \gamma_{(h,l_1)} (3\tau)})F(e^{2\pi i \gamma_{(9h,l_1)} (27\tau)})^2}\\ & \qquad \times e^{2\pi i (2h/k)} e^{\pi i (s(h,3l_1) + s(3h,l_1) - s(h,l_1) - 2s(9h,l_1))} e^{\frac{\pi}{12k}(-\frac{5}{3z} - z)}. \end{aligned} \end{align} $$
Case 3:
![]() $\mathrm {gcd}(k,27)=9$
. Let
$\mathrm {gcd}(k,27)=9$
. Let
![]() $k = 9l_2.$
It follows that
$k = 9l_2.$
It follows that
 $$ \begin{align*} \begin{aligned} \frac{F(e^{2\pi i \tau})F(e^{2\pi i (27\tau)})}{F(e^{2\pi i (9\tau)})^3} &= \frac{\sqrt{3}}{\sqrt{z}} \frac{F(e^{2\pi i \gamma_{(h,9l_2)} (\tau)})F(e^{2\pi i \gamma_{(3h,l_2)} (27\tau)})}{F(e^{2\pi i \gamma_{(h,l_2)} (9\tau)})^3}\\ &\quad \times e^{\pi i (s(h,9l_2) + s(3h,l_2) - 3s(h,l_2))} e^{\frac{\pi}{12k}(-\frac{23}{z} - z)} \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \frac{F(e^{2\pi i \tau})F(e^{2\pi i (27\tau)})}{F(e^{2\pi i (9\tau)})^3} &= \frac{\sqrt{3}}{\sqrt{z}} \frac{F(e^{2\pi i \gamma_{(h,9l_2)} (\tau)})F(e^{2\pi i \gamma_{(3h,l_2)} (27\tau)})}{F(e^{2\pi i \gamma_{(h,l_2)} (9\tau)})^3}\\ &\quad \times e^{\pi i (s(h,9l_2) + s(3h,l_2) - 3s(h,l_2))} e^{\frac{\pi}{12k}(-\frac{23}{z} - z)} \end{aligned} \end{align*} $$
and
 $$ \begin{align*} \begin{aligned} &e^{2\pi i (2\tau)} \frac{F(e^{2\pi i \tau})F(e^{2\pi i (9\tau)})}{F(e^{2\pi i (3\tau)})F(e^{2\pi i (27\tau)})^2}\\ &\quad=\frac{1}{3 \sqrt{z}} \frac{F(e^{2\pi i \gamma_{(h,9l_2)} (\tau)})F(e^{2\pi i \gamma_{(h,l_2)} (9\tau)})}{F(e^{2\pi i \gamma_{(h,3l_2)} (3\tau)})F(e^{2\pi i \gamma_{(3h,l_2)} (27\tau)})^2}\\ &\qquad \times e^{2\pi i (2h/k)} e^{\pi i (s(h,9l_2) + s(h,l_2) - s(h,3l_1) - 2s(3h,l_2))} e^{\frac{\pi}{12k}(\frac{1}{z} - z)}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} &e^{2\pi i (2\tau)} \frac{F(e^{2\pi i \tau})F(e^{2\pi i (9\tau)})}{F(e^{2\pi i (3\tau)})F(e^{2\pi i (27\tau)})^2}\\ &\quad=\frac{1}{3 \sqrt{z}} \frac{F(e^{2\pi i \gamma_{(h,9l_2)} (\tau)})F(e^{2\pi i \gamma_{(h,l_2)} (9\tau)})}{F(e^{2\pi i \gamma_{(h,3l_2)} (3\tau)})F(e^{2\pi i \gamma_{(3h,l_2)} (27\tau)})^2}\\ &\qquad \times e^{2\pi i (2h/k)} e^{\pi i (s(h,9l_2) + s(h,l_2) - s(h,3l_1) - 2s(3h,l_2))} e^{\frac{\pi}{12k}(\frac{1}{z} - z)}. \end{aligned} \end{align*} $$
Case 4:
![]() $\mathrm {gcd}(k,27)=27$
. Let
$\mathrm {gcd}(k,27)=27$
. Let
![]() $k = 27l_3.$
We have
$k = 27l_3.$
We have
 $$ \begin{align} \begin{aligned} \frac{F(e^{2\pi i \tau})F(e^{2\pi i (27\tau)})}{F(e^{2\pi i (9\tau)})^3} = & \frac{1}{\sqrt{z}} \frac{F(e^{2\pi i \gamma_{(h,27l_3)} (\tau)})F(e^{2\pi i \gamma_{(h,l_3)} (27\tau)})}{F(e^{2\pi i \gamma_{(h,3l_3)} (9\tau)})^3} \\ & \times e^{\pi i (s(h,27l_3) + s(h,l_3) - 3s(h,3l_3))} e^{\frac{\pi}{12k}(\frac{1}{z} - z)} \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \frac{F(e^{2\pi i \tau})F(e^{2\pi i (27\tau)})}{F(e^{2\pi i (9\tau)})^3} = & \frac{1}{\sqrt{z}} \frac{F(e^{2\pi i \gamma_{(h,27l_3)} (\tau)})F(e^{2\pi i \gamma_{(h,l_3)} (27\tau)})}{F(e^{2\pi i \gamma_{(h,3l_3)} (9\tau)})^3} \\ & \times e^{\pi i (s(h,27l_3) + s(h,l_3) - 3s(h,3l_3))} e^{\frac{\pi}{12k}(\frac{1}{z} - z)} \end{aligned} \end{align} $$
and
 $$ \begin{align*} \begin{aligned} &e^{2\pi i (2\tau)} \frac{F(e^{2\pi i \tau})F(e^{2\pi i (9\tau)})}{F(e^{2\pi i (3\tau)})F(e^{2\pi i (27\tau)})^2}\\ &\quad=\frac{1}{\sqrt{z}} \frac{F(e^{2\pi i \gamma_{(h,27l_3)} (\tau)})F(e^{2\pi i \gamma_{(h,3l_3)} (9\tau)})}{F(e^{2\pi i \gamma_{(h,9l_3)} (3\tau)})F(e^{2\pi i \gamma_{(h,l_3)} (27\tau)})^2} \\ &\qquad\times e^{2\pi i (2h/k)} e^{\pi i (s(h,27l_3) + s(h,3l_3) - s(h,9l_3) - 2s(h,l_3))} e^{\frac{\pi}{12k}(-\frac{47}{z} -z)}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} &e^{2\pi i (2\tau)} \frac{F(e^{2\pi i \tau})F(e^{2\pi i (9\tau)})}{F(e^{2\pi i (3\tau)})F(e^{2\pi i (27\tau)})^2}\\ &\quad=\frac{1}{\sqrt{z}} \frac{F(e^{2\pi i \gamma_{(h,27l_3)} (\tau)})F(e^{2\pi i \gamma_{(h,3l_3)} (9\tau)})}{F(e^{2\pi i \gamma_{(h,9l_3)} (3\tau)})F(e^{2\pi i \gamma_{(h,l_3)} (27\tau)})^2} \\ &\qquad\times e^{2\pi i (2h/k)} e^{\pi i (s(h,27l_3) + s(h,3l_3) - s(h,9l_3) - 2s(h,l_3))} e^{\frac{\pi}{12k}(-\frac{47}{z} -z)}. \end{aligned} \end{align*} $$
From the above transformation formulas for g and h, we see that the integrands of the integrals in
![]() $S_2(A), S_2(B),S_3(A)$
, and
$S_2(A), S_2(B),S_3(A)$
, and
![]() $S_4(B)$
have factors of the forms
$S_4(B)$
have factors of the forms
![]() $e^{\frac {\delta }{z}}$
with
$e^{\frac {\delta }{z}}$
with
![]() $\delta <0.$
For these integrals, we use (2.3), (2.5), (2.6), and (2.9) to give bounds. However, since the integrands of the integrals in
$\delta <0.$
For these integrals, we use (2.3), (2.5), (2.6), and (2.9) to give bounds. However, since the integrands of the integrals in
![]() $S_1(A), S_1(B), S_3(B)$
, and
$S_1(A), S_1(B), S_3(B)$
, and
![]() $S_4(A)$
contain factors of the forms
$S_4(A)$
contain factors of the forms
![]() $e^{\frac {\delta }{z}}$
with
$e^{\frac {\delta }{z}}$
with
![]() $\delta>0,$
we split these integrals into two parts and then apply Lemma 2.2, (2.3), (2.5), (2.6), and (2.10) to estimate the second parts. For the first parts, we employ Lemma 2.3 to tackle the integrals. It should be mentioned that our main term
$\delta>0,$
we split these integrals into two parts and then apply Lemma 2.2, (2.3), (2.5), (2.6), and (2.10) to estimate the second parts. For the first parts, we employ Lemma 2.3 to tackle the integrals. It should be mentioned that our main term
![]() $P(n)$
(in Subsection 3.3) originates from
$P(n)$
(in Subsection 3.3) originates from
![]() $S_3(B).$
$S_3(B).$
3.2 Bounding
 $S_2(A)$
,
$S_2(A)$
,
 $S_2(B)$
,
$S_2(B)$
,
 $S_3(A)$
, and
$S_3(A)$
, and
 $S_4(B)$
$S_4(B)$
For
![]() $S_2(A)$
, we apply (3.7) to deduce that
$S_2(A)$
, we apply (3.7) to deduce that
 $$ \begin{align*} \begin{aligned} A = & \frac{1}{\sqrt{3}} z^{-\frac{1}{2}} e^{\pi i (s(h,3l_1) + s(9h,l_1) - 3s(3h,l_1))} e^{\frac{\pi}{12k} \left(-\frac{5}{3z}-z\right)} \\ & \times \frac{F(e^{2\pi i \gamma_{(h,3l_1)} (\tau)})F(e^{2\pi i \gamma_{(9h,l_1)} (27\tau)})}{F(e^{2\pi i \gamma_{(3h,l_1)} (9\tau)})^3} e^{2 \pi n \varrho} e^{-2 \pi i n \varphi} \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} A = & \frac{1}{\sqrt{3}} z^{-\frac{1}{2}} e^{\pi i (s(h,3l_1) + s(9h,l_1) - 3s(3h,l_1))} e^{\frac{\pi}{12k} \left(-\frac{5}{3z}-z\right)} \\ & \times \frac{F(e^{2\pi i \gamma_{(h,3l_1)} (\tau)})F(e^{2\pi i \gamma_{(9h,l_1)} (27\tau)})}{F(e^{2\pi i \gamma_{(3h,l_1)} (9\tau)})^3} e^{2 \pi n \varrho} e^{-2 \pi i n \varphi} \end{aligned} \end{align*} $$
with
![]() $k=3l_1$
. Using (2.3), (2.5), (2.6), and (2.9), we find that
$k=3l_1$
. Using (2.3), (2.5), (2.6), and (2.9), we find that
 $$ \begin{align*} \begin{aligned} |A| \leq & \frac{1}{\sqrt{3}} F(e^{-2\pi(\frac{1}{k})\mathrm{Re}(\frac{1}{z})}) F(e^{-2\pi(\frac{3}{k})\mathrm{Re}(\frac{1}{9z})}) F(e^{-2\pi(\frac{3}{k})\mathrm{Re}(\frac{1}{3z})})^3 \\ & \times e^{-\frac{5\pi}{36k}\mathrm{Re}(\frac{1}{z})} e^{-\frac{\pi}{12k}\mathrm{Re}(z)} |z|^{-\frac{1}{2}} e^{2\pi n \varrho} \\ \leq & \frac{1}{\sqrt{3}} \mathrm{exp}\left(\frac{2\pi^2 e^{-\pi}}{3(1-e^{-\pi})} + \frac{\pi^2 e^{-\pi/3}}{6(1-e^{-\pi/3})}\right) \times e^{-\frac{5\pi}{72}} e^{2\pi(n-\frac{1}{24})\varrho} k^{-\frac{1}{2}} N \\ \leq & \frac{1}{\sqrt{3}} e^{0.969} e^{2\pi(n-\frac{1}{24})\varrho} k^{-\frac{1}{2}} N. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} |A| \leq & \frac{1}{\sqrt{3}} F(e^{-2\pi(\frac{1}{k})\mathrm{Re}(\frac{1}{z})}) F(e^{-2\pi(\frac{3}{k})\mathrm{Re}(\frac{1}{9z})}) F(e^{-2\pi(\frac{3}{k})\mathrm{Re}(\frac{1}{3z})})^3 \\ & \times e^{-\frac{5\pi}{36k}\mathrm{Re}(\frac{1}{z})} e^{-\frac{\pi}{12k}\mathrm{Re}(z)} |z|^{-\frac{1}{2}} e^{2\pi n \varrho} \\ \leq & \frac{1}{\sqrt{3}} \mathrm{exp}\left(\frac{2\pi^2 e^{-\pi}}{3(1-e^{-\pi})} + \frac{\pi^2 e^{-\pi/3}}{6(1-e^{-\pi/3})}\right) \times e^{-\frac{5\pi}{72}} e^{2\pi(n-\frac{1}{24})\varrho} k^{-\frac{1}{2}} N \\ \leq & \frac{1}{\sqrt{3}} e^{0.969} e^{2\pi(n-\frac{1}{24})\varrho} k^{-\frac{1}{2}} N. \end{aligned} \end{align*} $$
So we have
 $$ \begin{align*} \begin{aligned} |S_2(A)| \leq & \sum_{\substack{1 \leq k \leq N \\ (k,27) = 3}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} \int_{\xi_{h,k}} \frac{1}{\sqrt{3}} e^{0.969} e^{2\pi(n-\frac{1}{24})\varrho} k^{-\frac{1}{2}} N d\varphi \\ \leq & \sum_{\substack{1 \leq k \leq N \\ (k,27) = 3}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} \frac{1}{\sqrt{3}} e^{0.969} e^{2\pi(n-\frac{1}{24})\varrho} \frac{2}{k^{\frac{3}{2}}} \\ \leq & \frac{2}{\sqrt{3}} e^{0.969} e^{2\pi(n-\frac{1}{24})\varrho} \sum_{1 \leq k \leq N} k^{-\frac{1}{2}} \\ \leq & \frac{4}{\sqrt{3}} e^{0.969} e^{2\pi(n-\frac{1}{24})\varrho} N^{\frac{1}{2}}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} |S_2(A)| \leq & \sum_{\substack{1 \leq k \leq N \\ (k,27) = 3}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} \int_{\xi_{h,k}} \frac{1}{\sqrt{3}} e^{0.969} e^{2\pi(n-\frac{1}{24})\varrho} k^{-\frac{1}{2}} N d\varphi \\ \leq & \sum_{\substack{1 \leq k \leq N \\ (k,27) = 3}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} \frac{1}{\sqrt{3}} e^{0.969} e^{2\pi(n-\frac{1}{24})\varrho} \frac{2}{k^{\frac{3}{2}}} \\ \leq & \frac{2}{\sqrt{3}} e^{0.969} e^{2\pi(n-\frac{1}{24})\varrho} \sum_{1 \leq k \leq N} k^{-\frac{1}{2}} \\ \leq & \frac{4}{\sqrt{3}} e^{0.969} e^{2\pi(n-\frac{1}{24})\varrho} N^{\frac{1}{2}}. \end{aligned} \end{align*} $$
For
![]() $S_2(B)$
, we apply (3.8) to give
$S_2(B)$
, we apply (3.8) to give
 $$ \begin{align*} \begin{aligned} B = & \frac{1}{3 \sqrt{3}} z^{-\frac{1}{2}} e^{2\pi i (2h/k)} e^{\pi i (s(h,3l_1) + s(3h,l_1) - s(h,l_1) - 2s(9h,l_1))} e^{\frac{\pi}{12k}(-\frac{5}{3z} - z)} \\ & \times \frac{F(e^{2\pi i \gamma_{(h,3l_1)} (\tau)})F(e^{2\pi i \gamma_{(3h,l_1)} (9\tau)})}{F(e^{2\pi i \gamma_{(h,l_1)} (3\tau)})F(e^{2\pi i \gamma_{(9h,l_1)} (27\tau)})^2} e^{2 \pi n \varrho} e^{-2 \pi i n \varphi} \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} B = & \frac{1}{3 \sqrt{3}} z^{-\frac{1}{2}} e^{2\pi i (2h/k)} e^{\pi i (s(h,3l_1) + s(3h,l_1) - s(h,l_1) - 2s(9h,l_1))} e^{\frac{\pi}{12k}(-\frac{5}{3z} - z)} \\ & \times \frac{F(e^{2\pi i \gamma_{(h,3l_1)} (\tau)})F(e^{2\pi i \gamma_{(3h,l_1)} (9\tau)})}{F(e^{2\pi i \gamma_{(h,l_1)} (3\tau)})F(e^{2\pi i \gamma_{(9h,l_1)} (27\tau)})^2} e^{2 \pi n \varrho} e^{-2 \pi i n \varphi} \end{aligned} \end{align*} $$
with
![]() $k=3l_1$
. Using (2.3), (2.5), (2.6), and (2.9), we find that
$k=3l_1$
. Using (2.3), (2.5), (2.6), and (2.9), we find that
 $$ \begin{align*} \begin{aligned} |B| \leq & \frac{1}{3\sqrt{3}} F(e^{-2\pi(\frac{1}{k})\mathrm{Re}(\frac{1}{z})}) F(e^{-2\pi(\frac{3}{k})\mathrm{Re}(\frac{1}{3z})}) F(e^{-2\pi(\frac{3}{k})\mathrm{Re}(\frac{1}{z})}) F(e^{-2\pi(\frac{3}{k})\mathrm{Re}(\frac{1}{9z})})^2 \\ & \times e^{-\frac{5\pi}{36k}\mathrm{Re}(\frac{1}{z})} e^{-\frac{\pi}{12k}\mathrm{Re}(z)} |z|^{-\frac{1}{2}} e^{2\pi n \varrho} \\ \leq & \frac{1}{3\sqrt{3}} \mathrm{exp}\left(\frac{\pi^2 e^{-\pi}}{3(1-e^{-\pi})} + \frac{\pi^2 e^{-3\pi}}{6(1-e^{-3\pi})} + \frac{\pi^2 e^{-\pi/3}}{3(1-e^{-\pi/3})}\right) e^{-\frac{5\pi}{72}} e^{2\pi(n-\frac{1}{24})\varrho} k^{-\frac{1}{2}} N \\ \leq & \frac{1}{3\sqrt{3}} e^{1.710} e^{2\pi(n-\frac{1}{24})\varrho} k^{-\frac{1}{2}} N \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} |B| \leq & \frac{1}{3\sqrt{3}} F(e^{-2\pi(\frac{1}{k})\mathrm{Re}(\frac{1}{z})}) F(e^{-2\pi(\frac{3}{k})\mathrm{Re}(\frac{1}{3z})}) F(e^{-2\pi(\frac{3}{k})\mathrm{Re}(\frac{1}{z})}) F(e^{-2\pi(\frac{3}{k})\mathrm{Re}(\frac{1}{9z})})^2 \\ & \times e^{-\frac{5\pi}{36k}\mathrm{Re}(\frac{1}{z})} e^{-\frac{\pi}{12k}\mathrm{Re}(z)} |z|^{-\frac{1}{2}} e^{2\pi n \varrho} \\ \leq & \frac{1}{3\sqrt{3}} \mathrm{exp}\left(\frac{\pi^2 e^{-\pi}}{3(1-e^{-\pi})} + \frac{\pi^2 e^{-3\pi}}{6(1-e^{-3\pi})} + \frac{\pi^2 e^{-\pi/3}}{3(1-e^{-\pi/3})}\right) e^{-\frac{5\pi}{72}} e^{2\pi(n-\frac{1}{24})\varrho} k^{-\frac{1}{2}} N \\ \leq & \frac{1}{3\sqrt{3}} e^{1.710} e^{2\pi(n-\frac{1}{24})\varrho} k^{-\frac{1}{2}} N \end{aligned} \end{align*} $$
and
 $$ \begin{align*} \begin{aligned} |S_2(B)| \leq & \sum_{\substack{1 \leq k \leq N \\ (k,27) = 3}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} \int_{\xi_{h,k}} \frac{1}{3\sqrt{3}} e^{1.710} e^{2\pi(n-\frac{1}{24})\varrho} k^{-\frac{1}{2}} N d\varphi \\ \leq & \sum_{\substack{1 \leq k \leq N \\ (k,27) = 3}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} \frac{1}{3\sqrt{3}} e^{1.710} e^{2\pi(n-\frac{1}{24})\varrho} \frac{2}{k^{\frac{3}{2}}} \\ \leq & \frac{2}{3\sqrt{3}} e^{1.710} e^{2\pi(n-\frac{1}{24})\varrho} \sum_{1 \leq k \leq N} k^{-\frac{1}{2}} \\ \leq & \frac{4}{3\sqrt{3}} e^{1.710} e^{2\pi(n-\frac{1}{24})\varrho} N^{\frac{1}{2}}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} |S_2(B)| \leq & \sum_{\substack{1 \leq k \leq N \\ (k,27) = 3}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} \int_{\xi_{h,k}} \frac{1}{3\sqrt{3}} e^{1.710} e^{2\pi(n-\frac{1}{24})\varrho} k^{-\frac{1}{2}} N d\varphi \\ \leq & \sum_{\substack{1 \leq k \leq N \\ (k,27) = 3}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} \frac{1}{3\sqrt{3}} e^{1.710} e^{2\pi(n-\frac{1}{24})\varrho} \frac{2}{k^{\frac{3}{2}}} \\ \leq & \frac{2}{3\sqrt{3}} e^{1.710} e^{2\pi(n-\frac{1}{24})\varrho} \sum_{1 \leq k \leq N} k^{-\frac{1}{2}} \\ \leq & \frac{4}{3\sqrt{3}} e^{1.710} e^{2\pi(n-\frac{1}{24})\varrho} N^{\frac{1}{2}}. \end{aligned} \end{align*} $$
Similarly, for
![]() $S_3(A)$
and
$S_3(A)$
and
![]() $S_4(B)$
, we get
$S_4(B)$
, we get
and
3.3 Tackling
 $S_1(A)$
,
$S_1(A)$
,
 $S_1(B)$
,
$S_1(B)$
,
 $S_3(B)$
, and
$S_3(B)$
, and
 $S_4(A)$
$S_4(A)$
For
![]() $S_1(A)$
, set
$S_1(A)$
, set
We apply (3.5) to deduce
 $$ \begin{align*} S_1(A) &= \sum_{\substack{1 \leq k \leq N \\ (k,27) = 1}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} e^{-2\pi i nh/k} \int_{\xi_{h,k}} \frac{F(e^{2\pi i \tau})F(e^{2\pi i (27\tau)})}{F(e^{2\pi i (9\tau)})^3} e^{2\pi n \varrho} e^{-2\pi i n \varphi} d\varphi \\ &= \sum_{\substack{1 \leq k \leq N \\ (k,27) = 1}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} e^{-2\pi i nh/k} \omega^{(1)}_{(h,k)} \int_{\xi_{h,k}} \frac{1}{3 \sqrt{3} \sqrt{z}} e^{\frac{\pi}{12k}(\frac{19}{27z} - z)} \\ & \quad\times \frac{F(e^{2\pi i \gamma_{(h,k)} (\tau)})F(e^{2\pi i \gamma_{(27h,k)} (27\tau)})}{F(e^{2\pi i \gamma_{(9h,k)} (9\tau)})^3} e^{2\pi n \varrho} e^{-2\pi i n \varphi} d\varphi \\ \notag &= \sum_{\substack{1 \leq k \leq N \\ (k,27) = 1}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} e^{-2\pi i nh/k} \omega^{(1)}_{(h,k)} \int_{\xi_{h,k}} \frac{1}{3 \sqrt{3} \sqrt{z}} e^{\frac{\pi}{12k}(\frac{19}{27z} - z)} e^{2\pi n \varrho} e^{-2\pi i n \varphi} d\varphi \\ \notag &\quad + \sum_{\substack{1 \leq k \leq N \\ (k,27) = 1}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} e^{-2\pi i nh/k} \omega^{(1)}_{(h,k)} \int_{\xi_{h,k}} \frac{1}{3 \sqrt{3} \sqrt{z}} e^{\frac{\pi}{12k}(\frac{19}{27z} - z)} \\ \notag & \quad\times \left(\frac{F(e^{2\pi i \gamma_{(h,k)} (\tau)})F(e^{2\pi i \gamma_{(27h,k)} (27\tau)})}{F(e^{2\pi i \gamma_{(9h,k)} (9\tau)})^3} - 1 \right) e^{2\pi n \varrho} e^{-2\pi i n \varphi} d\varphi \\ \notag & =: T_{1} + T_{2}. \notag \end{align*} $$
$$ \begin{align*} S_1(A) &= \sum_{\substack{1 \leq k \leq N \\ (k,27) = 1}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} e^{-2\pi i nh/k} \int_{\xi_{h,k}} \frac{F(e^{2\pi i \tau})F(e^{2\pi i (27\tau)})}{F(e^{2\pi i (9\tau)})^3} e^{2\pi n \varrho} e^{-2\pi i n \varphi} d\varphi \\ &= \sum_{\substack{1 \leq k \leq N \\ (k,27) = 1}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} e^{-2\pi i nh/k} \omega^{(1)}_{(h,k)} \int_{\xi_{h,k}} \frac{1}{3 \sqrt{3} \sqrt{z}} e^{\frac{\pi}{12k}(\frac{19}{27z} - z)} \\ & \quad\times \frac{F(e^{2\pi i \gamma_{(h,k)} (\tau)})F(e^{2\pi i \gamma_{(27h,k)} (27\tau)})}{F(e^{2\pi i \gamma_{(9h,k)} (9\tau)})^3} e^{2\pi n \varrho} e^{-2\pi i n \varphi} d\varphi \\ \notag &= \sum_{\substack{1 \leq k \leq N \\ (k,27) = 1}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} e^{-2\pi i nh/k} \omega^{(1)}_{(h,k)} \int_{\xi_{h,k}} \frac{1}{3 \sqrt{3} \sqrt{z}} e^{\frac{\pi}{12k}(\frac{19}{27z} - z)} e^{2\pi n \varrho} e^{-2\pi i n \varphi} d\varphi \\ \notag &\quad + \sum_{\substack{1 \leq k \leq N \\ (k,27) = 1}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} e^{-2\pi i nh/k} \omega^{(1)}_{(h,k)} \int_{\xi_{h,k}} \frac{1}{3 \sqrt{3} \sqrt{z}} e^{\frac{\pi}{12k}(\frac{19}{27z} - z)} \\ \notag & \quad\times \left(\frac{F(e^{2\pi i \gamma_{(h,k)} (\tau)})F(e^{2\pi i \gamma_{(27h,k)} (27\tau)})}{F(e^{2\pi i \gamma_{(9h,k)} (9\tau)})^3} - 1 \right) e^{2\pi n \varrho} e^{-2\pi i n \varphi} d\varphi \\ \notag & =: T_{1} + T_{2}. \notag \end{align*} $$
 $$ \begin{align*} \begin{aligned} \left| e^{\frac{\pi}{12k}\left(\frac{19}{27z}\right)} \left(\frac{F(e^{2\pi i \gamma_{(h,k)} (\tau)})F(e^{2\pi i \gamma_{(27h,k)} (27\tau)})}{F(e^{2\pi i \gamma_{(9h,k)} (9\tau)})^3} - 1 \right) \right| \leq e^{\frac{19\pi}{27\times12k}\mathrm{Re}\left(\frac{1}{z}\right)} \left( e^{f(k,z)}- 1\right), \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \left| e^{\frac{\pi}{12k}\left(\frac{19}{27z}\right)} \left(\frac{F(e^{2\pi i \gamma_{(h,k)} (\tau)})F(e^{2\pi i \gamma_{(27h,k)} (27\tau)})}{F(e^{2\pi i \gamma_{(9h,k)} (9\tau)})^3} - 1 \right) \right| \leq e^{\frac{19\pi}{27\times12k}\mathrm{Re}\left(\frac{1}{z}\right)} \left( e^{f(k,z)}- 1\right), \end{aligned} \end{align*} $$
where
 $$ \begin{align*}f(k,z)=\frac{\pi^2 e^{-2\pi \frac{1}{k} \mathrm{Re}(\frac{1}{z})}}{6(1-e^{-2\pi \frac{1}{k} \mathrm{Re}(\frac{1}{z})})} + \frac{\pi^2 e^{-2\pi \frac{1}{27k} \mathrm{Re}(\frac{1}{z})}}{6(1-e^{-2\pi \frac{1}{27k} \mathrm{Re}(\frac{1}{z})})} + \frac{3\pi^2 e^{-2\pi \frac{1}{9k} \mathrm{Re}(\frac{1}{z})}}{6(1-e^{-2\pi \frac{1}{9k} \mathrm{Re}(\frac{1}{z})})} .\end{align*} $$
$$ \begin{align*}f(k,z)=\frac{\pi^2 e^{-2\pi \frac{1}{k} \mathrm{Re}(\frac{1}{z})}}{6(1-e^{-2\pi \frac{1}{k} \mathrm{Re}(\frac{1}{z})})} + \frac{\pi^2 e^{-2\pi \frac{1}{27k} \mathrm{Re}(\frac{1}{z})}}{6(1-e^{-2\pi \frac{1}{27k} \mathrm{Re}(\frac{1}{z})})} + \frac{3\pi^2 e^{-2\pi \frac{1}{9k} \mathrm{Re}(\frac{1}{z})}}{6(1-e^{-2\pi \frac{1}{9k} \mathrm{Re}(\frac{1}{z})})} .\end{align*} $$
Let
Then,
 $$ \begin{align*} \begin{aligned} & \left| e^{\frac{\pi}{12k}\left(\frac{19}{27z}\right)} \left(\frac{F(e^{2\pi i \gamma_{(h,k)} (\tau)})F(e^{2\pi i \gamma_{(27h,k)} (27\tau)})}{F(e^{2\pi i \gamma_{(9h,k)} (9\tau)})^3} - 1 \right) \right| \\ &\quad \leq \frac{1}{x} \left(\mathrm{exp}\left(\frac{\pi^2 x^{\frac{648}{19}}}{6(1-x^{\frac{648}{19}})}+\frac{\pi^2 x^{\frac{24}{19}}}{6(1-x^{\frac{24}{19}})}+\frac{3\pi^2 x^{\frac{72}{19}}}{6(1-x^{\frac{72}{19}})}\right) - 1\right)=: W_1(x). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} & \left| e^{\frac{\pi}{12k}\left(\frac{19}{27z}\right)} \left(\frac{F(e^{2\pi i \gamma_{(h,k)} (\tau)})F(e^{2\pi i \gamma_{(27h,k)} (27\tau)})}{F(e^{2\pi i \gamma_{(9h,k)} (9\tau)})^3} - 1 \right) \right| \\ &\quad \leq \frac{1}{x} \left(\mathrm{exp}\left(\frac{\pi^2 x^{\frac{648}{19}}}{6(1-x^{\frac{648}{19}})}+\frac{\pi^2 x^{\frac{24}{19}}}{6(1-x^{\frac{24}{19}})}+\frac{3\pi^2 x^{\frac{72}{19}}}{6(1-x^{\frac{72}{19}})}\right) - 1\right)=: W_1(x). \end{aligned} \end{align*} $$
By Lemma 2.2 and (2.5), we get
 $$ \begin{align*} \begin{aligned} W_1(x) & \leq W_1(e^{-\frac{19\pi}{648}}) = e^{\frac{19\pi}{648}} \left(\mathrm{exp}\left(\frac{\pi^2 e^{-\pi}}{6(1-e^{-\pi})}+\frac{\pi^2 e^{-\pi/27}}{6(1-e^{-\pi/27})}+\frac{3\pi^2 e^{-\pi/9}}{6(1-e^{-\pi/9})}\right) - 1\right) \\ & \leq 9.819 \times 10^{10}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} W_1(x) & \leq W_1(e^{-\frac{19\pi}{648}}) = e^{\frac{19\pi}{648}} \left(\mathrm{exp}\left(\frac{\pi^2 e^{-\pi}}{6(1-e^{-\pi})}+\frac{\pi^2 e^{-\pi/27}}{6(1-e^{-\pi/27})}+\frac{3\pi^2 e^{-\pi/9}}{6(1-e^{-\pi/9})}\right) - 1\right) \\ & \leq 9.819 \times 10^{10}. \end{aligned} \end{align*} $$
Then, by (2.6),
 $$ \begin{align*} \begin{aligned} |T_{2}| \leq & \sum_{\substack{1 \leq k \leq N \\ (k,27) = 1}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} \int_{\xi_{h,k}} 1.890 \times 10^{10} e^{-\frac{\pi}{12k}\mathrm{Re}(z)} |z|^{-1/2} e^{-2\pi i n \varrho} d\varphi \\ \leq & \sum_{\substack{1 \leq k \leq N \\ (k,27) = 1}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} 1.890 \times 10^{10} e^{2\pi (n - 1/24) \varrho} \frac{2}{k^{3/2}} \\ \leq & \sum_{\substack{1 \leq k \leq N \\ (k,27) = 1}} 1.890 \times 10^{10} e^{2\pi (n - 1/24) \varrho} \frac{2}{k^{1/2}} \\ \leq & 7.560 \times 10^{10} e^{2\pi (n - 1/24) \varrho} N^{1/2}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} |T_{2}| \leq & \sum_{\substack{1 \leq k \leq N \\ (k,27) = 1}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} \int_{\xi_{h,k}} 1.890 \times 10^{10} e^{-\frac{\pi}{12k}\mathrm{Re}(z)} |z|^{-1/2} e^{-2\pi i n \varrho} d\varphi \\ \leq & \sum_{\substack{1 \leq k \leq N \\ (k,27) = 1}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} 1.890 \times 10^{10} e^{2\pi (n - 1/24) \varrho} \frac{2}{k^{3/2}} \\ \leq & \sum_{\substack{1 \leq k \leq N \\ (k,27) = 1}} 1.890 \times 10^{10} e^{2\pi (n - 1/24) \varrho} \frac{2}{k^{1/2}} \\ \leq & 7.560 \times 10^{10} e^{2\pi (n - 1/24) \varrho} N^{1/2}. \end{aligned} \end{align*} $$
Similarly, we use (3.6) to derive that
where
 $$ \begin{align*} \begin{aligned} R_{1} := \sum_{\substack{1 \leq k \leq N \\ (k,27) = 1}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} e^{-2\pi i (n-2)h/k} \omega^{(2)}_{(h,k)} \int_{\xi_{h,k}} \frac{1}{9 \sqrt{3} \sqrt{z}} e^{\frac{\pi}{12k}(\frac{19}{27z} - z)} e^{2\pi n \varrho} e^{-2\pi i n \varphi} d\varphi, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} R_{1} := \sum_{\substack{1 \leq k \leq N \\ (k,27) = 1}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} e^{-2\pi i (n-2)h/k} \omega^{(2)}_{(h,k)} \int_{\xi_{h,k}} \frac{1}{9 \sqrt{3} \sqrt{z}} e^{\frac{\pi}{12k}(\frac{19}{27z} - z)} e^{2\pi n \varrho} e^{-2\pi i n \varphi} d\varphi, \end{aligned} \end{align*} $$
and
Here,
![]() $\omega ^{(2)}_{(h,k)} := e^{\pi i (s(h,k) + s(9h,k) - s(3h,k) - 2s(27h,k))}.$
$\omega ^{(2)}_{(h,k)} := e^{\pi i (s(h,k) + s(9h,k) - s(3h,k) - 2s(27h,k))}.$
Using the software Mathematica, we find thatFootnote 2
where
![]() $0\leq h < k \leq 17, (k,3)=1$
, and
$0\leq h < k \leq 17, (k,3)=1$
, and
![]() $(h,k)=1.$
From this, we have
$(h,k)=1.$
From this, we have
 $$ \begin{align*} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} e^{-2\pi i nh/k} \omega^{(1)}_{(h,k)} = \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} e^{-2\pi i (n-2)h/k} \omega^{(2)}_{(h,k)} \end{align*} $$
$$ \begin{align*} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} e^{-2\pi i nh/k} \omega^{(1)}_{(h,k)} = \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} e^{-2\pi i (n-2)h/k} \omega^{(2)}_{(h,k)} \end{align*} $$
with
![]() $k \leq 17$
and
$k \leq 17$
and
![]() $\mathrm {gcd}(k,27)=1.$
Then,
$\mathrm {gcd}(k,27)=1.$
Then,
 $$ \begin{align*} \begin{aligned} |T_{1} - 3R_{1}| &= \bigg|\sum_{\substack{1 \leq k \leq N \\ (k,27) = 1}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} e^{-2\pi i nh/k} \omega^{(1)}_{(h,k)} \int_{\xi_{h,k}} \frac{1}{3 \sqrt{3} \sqrt{z}} e^{\frac{\pi}{12k}(\frac{19}{27z} - z)} e^{2\pi n \varrho} e^{-2\pi i n \varphi} d\varphi \\ &\quad - \big. \sum_{\substack{1 \leq k \leq N \\ (k,27) = 1}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} e^{-2\pi i (n-2)h/k} \omega^{(2)}_{(h,k)}\\&\quad \int_{\xi_{h,k}} \frac{1}{3 \sqrt{3} \sqrt{z}} e^{\frac{\pi}{12k}(\frac{19}{27z} - z)} e^{2\pi n \varrho} e^{-2\pi i n \varphi} d\varphi \bigg| \\& \leq \bigg|\sum_{\substack{19 \leq k \leq N \\ (k,27) = 1}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} e^{-2\pi i nh/k} \omega^{(1)}_{(h,k)} \int_{\xi_{h,k}} \frac{1}{3 \sqrt{3} \sqrt{z}} e^{\frac{\pi}{12k}(\frac{19}{27z} - z)} e^{2\pi n \varrho} e^{-2\pi i n \varphi} d\varphi\bigg| \\ &\quad + \bigg|\sum_{\substack{19 \leq k \leq N \\ (k,27) = 1}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} e^{-2\pi i (n-2)h/k} \omega^{(2)}_{(h,k)}\\&\quad \int_{\xi_{h,k}} \frac{1}{3 \sqrt{3} \sqrt{z}} e^{\frac{\pi}{12k}(\frac{19}{27z} - z)} e^{2\pi n \varrho} e^{-2\pi i n \varphi} d\varphi\bigg|. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} |T_{1} - 3R_{1}| &= \bigg|\sum_{\substack{1 \leq k \leq N \\ (k,27) = 1}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} e^{-2\pi i nh/k} \omega^{(1)}_{(h,k)} \int_{\xi_{h,k}} \frac{1}{3 \sqrt{3} \sqrt{z}} e^{\frac{\pi}{12k}(\frac{19}{27z} - z)} e^{2\pi n \varrho} e^{-2\pi i n \varphi} d\varphi \\ &\quad - \big. \sum_{\substack{1 \leq k \leq N \\ (k,27) = 1}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} e^{-2\pi i (n-2)h/k} \omega^{(2)}_{(h,k)}\\&\quad \int_{\xi_{h,k}} \frac{1}{3 \sqrt{3} \sqrt{z}} e^{\frac{\pi}{12k}(\frac{19}{27z} - z)} e^{2\pi n \varrho} e^{-2\pi i n \varphi} d\varphi \bigg| \\& \leq \bigg|\sum_{\substack{19 \leq k \leq N \\ (k,27) = 1}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} e^{-2\pi i nh/k} \omega^{(1)}_{(h,k)} \int_{\xi_{h,k}} \frac{1}{3 \sqrt{3} \sqrt{z}} e^{\frac{\pi}{12k}(\frac{19}{27z} - z)} e^{2\pi n \varrho} e^{-2\pi i n \varphi} d\varphi\bigg| \\ &\quad + \bigg|\sum_{\substack{19 \leq k \leq N \\ (k,27) = 1}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} e^{-2\pi i (n-2)h/k} \omega^{(2)}_{(h,k)}\\&\quad \int_{\xi_{h,k}} \frac{1}{3 \sqrt{3} \sqrt{z}} e^{\frac{\pi}{12k}(\frac{19}{27z} - z)} e^{2\pi n \varrho} e^{-2\pi i n \varphi} d\varphi\bigg|. \end{aligned} \end{align*} $$
By Lemma 2.3, we have
 $$ \begin{align*} &\sum_{\substack{19 \leq k \leq N \\ (k,27) = 1}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} \left|\int_{\xi_{h,k}} \frac{1}{3 \sqrt{3} \sqrt{z}} e^{\frac{\pi}{12k}(\frac{19}{27z} - z)} e^{2\pi n \varrho} e^{-2\pi i n \varphi} d\varphi\right| \\ \notag &\leq \sum_{\substack{19 \leq k \leq N \\ (k,27) = 1}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} \sqrt{\frac{2}{k(n-1/24)}} \left(\frac{19}{27}\right)^{1/4} \mathrm{cosh}\left(\frac{\pi}{k} \sqrt{\frac{19}{27}\times\frac{2}{3}\left(n-\frac{1}{24}\right)} \right) \\ &\quad+ \sum_{\substack{19 \leq k \leq N \\ (k,27) = 1}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} \sqrt{2} \pi^{-1} e^{19\pi/81} \frac{e^{2\pi (n-1/24) \varrho} N^{1/2}}{n-1/24} \\\notag &\leq \sum_{\substack{19 \leq k \leq N \\ (k,27) = 1}} \sqrt{\frac{2k}{n-1/24}} \mathrm{cosh}\left(\frac{\pi}{18} \sqrt{\frac{2}{3}\left(n-\frac{1}{24}\right)} \right) \\ \notag &\; + \sum_{\substack{19 \leq k \leq N \\ (k,27) = 1}} 1.2828 \frac{e^{2\pi (n-1/24) \varrho} k N^{1/2}}{n-1/24} \\ \notag & \leq N^{3/2} \sqrt{\frac{2}{n-1/24}} \mathrm{cosh}\left(\frac{\pi}{18} \sqrt{\frac{2}{3}\left(n-\frac{1}{24}\right)} \right) + 1.2828 \frac{e^{2\pi (n-1/24) \varrho} N^{5/2}}{n-1/24}. \notag \end{align*} $$
$$ \begin{align*} &\sum_{\substack{19 \leq k \leq N \\ (k,27) = 1}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} \left|\int_{\xi_{h,k}} \frac{1}{3 \sqrt{3} \sqrt{z}} e^{\frac{\pi}{12k}(\frac{19}{27z} - z)} e^{2\pi n \varrho} e^{-2\pi i n \varphi} d\varphi\right| \\ \notag &\leq \sum_{\substack{19 \leq k \leq N \\ (k,27) = 1}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} \sqrt{\frac{2}{k(n-1/24)}} \left(\frac{19}{27}\right)^{1/4} \mathrm{cosh}\left(\frac{\pi}{k} \sqrt{\frac{19}{27}\times\frac{2}{3}\left(n-\frac{1}{24}\right)} \right) \\ &\quad+ \sum_{\substack{19 \leq k \leq N \\ (k,27) = 1}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} \sqrt{2} \pi^{-1} e^{19\pi/81} \frac{e^{2\pi (n-1/24) \varrho} N^{1/2}}{n-1/24} \\\notag &\leq \sum_{\substack{19 \leq k \leq N \\ (k,27) = 1}} \sqrt{\frac{2k}{n-1/24}} \mathrm{cosh}\left(\frac{\pi}{18} \sqrt{\frac{2}{3}\left(n-\frac{1}{24}\right)} \right) \\ \notag &\; + \sum_{\substack{19 \leq k \leq N \\ (k,27) = 1}} 1.2828 \frac{e^{2\pi (n-1/24) \varrho} k N^{1/2}}{n-1/24} \\ \notag & \leq N^{3/2} \sqrt{\frac{2}{n-1/24}} \mathrm{cosh}\left(\frac{\pi}{18} \sqrt{\frac{2}{3}\left(n-\frac{1}{24}\right)} \right) + 1.2828 \frac{e^{2\pi (n-1/24) \varrho} N^{5/2}}{n-1/24}. \notag \end{align*} $$
So we have
 $$ \begin{align*} |T_{1} - 3R_{1}| \leq 2N^{3/2} \sqrt{\frac{2}{(n-1/24)}} \mathrm{cosh}\left(\frac{\pi}{18} \sqrt{\frac{2}{3}\left(n-\frac{1}{24}\right)} \right) + 2.5656 \frac{e^{2\pi (n-1/24) \varrho} N^{5/2}}{n-1/24}. \end{align*} $$
$$ \begin{align*} |T_{1} - 3R_{1}| \leq 2N^{3/2} \sqrt{\frac{2}{(n-1/24)}} \mathrm{cosh}\left(\frac{\pi}{18} \sqrt{\frac{2}{3}\left(n-\frac{1}{24}\right)} \right) + 2.5656 \frac{e^{2\pi (n-1/24) \varrho} N^{5/2}}{n-1/24}. \end{align*} $$
Setting
![]() $N:=\sqrt {2\pi (n-1/24)}$
, we obtain
$N:=\sqrt {2\pi (n-1/24)}$
, we obtain
 $$ \begin{align*} \begin{aligned} |T_{1} - 3R_{1}| &\leq 2 (2\pi)^{3/4} \sqrt{2} (n-1/24)^{(1/4)} (e^{\frac{\pi}{18} \sqrt{\frac{2}{3}(n-\frac{1}{24})}}+1)\\ &+ 2.5656 e (2\pi)^{5/4} (n-1/24)^{(1/4)} \\ &\leq 11.225 (n-1/24)^{(1/4)} e^{\frac{\pi}{18} \sqrt{\frac{2}{3}(n-\frac{1}{24})}} + 80.601 (n-1/24)^{(1/4)}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} |T_{1} - 3R_{1}| &\leq 2 (2\pi)^{3/4} \sqrt{2} (n-1/24)^{(1/4)} (e^{\frac{\pi}{18} \sqrt{\frac{2}{3}(n-\frac{1}{24})}}+1)\\ &+ 2.5656 e (2\pi)^{5/4} (n-1/24)^{(1/4)} \\ &\leq 11.225 (n-1/24)^{(1/4)} e^{\frac{\pi}{18} \sqrt{\frac{2}{3}(n-\frac{1}{24})}} + 80.601 (n-1/24)^{(1/4)}. \end{aligned} \end{align*} $$
For
![]() $S_3(B)$
, set
$S_3(B)$
, set
![]() $\Omega _{(h,k)} := e^{\pi i (s(h,9l_2) + s(h,l_2) - s(h,3l_1) - 2s(3h,l_2))}$
. We apply (3.1) to conclude that
$\Omega _{(h,k)} := e^{\pi i (s(h,9l_2) + s(h,l_2) - s(h,3l_1) - 2s(3h,l_2))}$
. We apply (3.1) to conclude that
 $$ \begin{align*} \begin{aligned}\! S_3(B)& = \!\sum_{\substack{1 \leq k \leq N \\ (k,27) = 9}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} \!\!e^{-2\pi i nh/k}\! \int_{\xi_{h,k}} \!e^{2\pi i (2\tau)} \frac{F(e^{2\pi i \tau})F(e^{2\pi i (9\tau)})}{F(e^{2\pi i (3\tau)})F(e^{2\pi i (27\tau)})^2} e^{2\pi n \varrho} e^{-2\pi i n \varphi} d\varphi \\ & = \sum_{\substack{1 \leq k \leq N \\ (k,27) = 9}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} e^{-2\pi i (n-2)h/k} \Omega_{(h,k)} \int_{\xi_{h,k}} \frac{1}{3 \sqrt{z}} e^{\frac{\pi}{12k}(\frac{1}{z} - z)} \\ & \quad \times \frac{F(e^{2\pi i \gamma_{(h,9l_2)} (\tau)})F(e^{2\pi i \gamma_{(h,l_2)} (9\tau)})}{F(e^{2\pi i \gamma_{(h,3l_2)} (3\tau)})F(e^{2\pi i \gamma_{(3h,l_2)} (27\tau)})^2} e^{2\pi n \varrho} e^{-2\pi i n \varphi} d\varphi \\ &= \sum_{\substack{1 \leq k \leq N \\ (k,27) = 9}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} e^{-2\pi i (n-2)h/k} \Omega_{(h,k)} \int_{\xi_{h,k}} \frac{1}{3 \sqrt{z}} e^{\frac{\pi}{12k}(\frac{1}{z} - z)} e^{2\pi n \varrho} e^{-2\pi i n \varphi} d\varphi \\ & \quad + \sum_{\substack{1 \leq k \leq N \\ (k,27) = 9}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} e^{-2\pi i (n-2)h/k} \Omega_{(h,k)} \int_{\xi_{h,k}} \frac{1}{3 \sqrt{z}} e^{\frac{\pi}{12k}(\frac{1}{z} - z)} \\ &\quad\times \left(\frac{F(e^{2\pi i \gamma_{(h,9l_2)} (\tau)})F(e^{2\pi i \gamma_{(h,l_2)} (9\tau)})}{F(e^{2\pi i \gamma_{(h,3l_2)} (3\tau)})F(e^{2\pi i \gamma_{(3h,l_2)} (27\tau)})^2} - 1 \right) e^{2\pi n \varrho} e^{-2\pi i n \varphi} d\varphi \\ & =:P_{1} + P_{2} \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned}\! S_3(B)& = \!\sum_{\substack{1 \leq k \leq N \\ (k,27) = 9}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} \!\!e^{-2\pi i nh/k}\! \int_{\xi_{h,k}} \!e^{2\pi i (2\tau)} \frac{F(e^{2\pi i \tau})F(e^{2\pi i (9\tau)})}{F(e^{2\pi i (3\tau)})F(e^{2\pi i (27\tau)})^2} e^{2\pi n \varrho} e^{-2\pi i n \varphi} d\varphi \\ & = \sum_{\substack{1 \leq k \leq N \\ (k,27) = 9}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} e^{-2\pi i (n-2)h/k} \Omega_{(h,k)} \int_{\xi_{h,k}} \frac{1}{3 \sqrt{z}} e^{\frac{\pi}{12k}(\frac{1}{z} - z)} \\ & \quad \times \frac{F(e^{2\pi i \gamma_{(h,9l_2)} (\tau)})F(e^{2\pi i \gamma_{(h,l_2)} (9\tau)})}{F(e^{2\pi i \gamma_{(h,3l_2)} (3\tau)})F(e^{2\pi i \gamma_{(3h,l_2)} (27\tau)})^2} e^{2\pi n \varrho} e^{-2\pi i n \varphi} d\varphi \\ &= \sum_{\substack{1 \leq k \leq N \\ (k,27) = 9}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} e^{-2\pi i (n-2)h/k} \Omega_{(h,k)} \int_{\xi_{h,k}} \frac{1}{3 \sqrt{z}} e^{\frac{\pi}{12k}(\frac{1}{z} - z)} e^{2\pi n \varrho} e^{-2\pi i n \varphi} d\varphi \\ & \quad + \sum_{\substack{1 \leq k \leq N \\ (k,27) = 9}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} e^{-2\pi i (n-2)h/k} \Omega_{(h,k)} \int_{\xi_{h,k}} \frac{1}{3 \sqrt{z}} e^{\frac{\pi}{12k}(\frac{1}{z} - z)} \\ &\quad\times \left(\frac{F(e^{2\pi i \gamma_{(h,9l_2)} (\tau)})F(e^{2\pi i \gamma_{(h,l_2)} (9\tau)})}{F(e^{2\pi i \gamma_{(h,3l_2)} (3\tau)})F(e^{2\pi i \gamma_{(3h,l_2)} (27\tau)})^2} - 1 \right) e^{2\pi n \varrho} e^{-2\pi i n \varphi} d\varphi \\ & =:P_{1} + P_{2} \end{aligned} \end{align*} $$
with
![]() $k=9l_2$
.
$k=9l_2$
.
For
![]() $P_2$
, by (2.10), we have
$P_2$
, by (2.10), we have
 $$ \begin{align*} \begin{aligned} \left| e^{\frac{\pi}{12k}(\frac{1}{z})} \left(\frac{F(e^{2\pi i \gamma_{(h,9l_2)} (\tau)})F(e^{2\pi i \gamma_{(h,l_2)} (9\tau)})}{F(e^{2\pi i \gamma_{(h,3l_2)} (3\tau)})F(e^{2\pi i \gamma_{(3h,l_2)} (27\tau)})^2} - 1 \right) \right| \leq e^{\frac{\pi}{12k}\mathrm{Re}\left(\frac{1}{z}\right)} \left( e^{g(k,z)}- 1\right), \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \left| e^{\frac{\pi}{12k}(\frac{1}{z})} \left(\frac{F(e^{2\pi i \gamma_{(h,9l_2)} (\tau)})F(e^{2\pi i \gamma_{(h,l_2)} (9\tau)})}{F(e^{2\pi i \gamma_{(h,3l_2)} (3\tau)})F(e^{2\pi i \gamma_{(3h,l_2)} (27\tau)})^2} - 1 \right) \right| \leq e^{\frac{\pi}{12k}\mathrm{Re}\left(\frac{1}{z}\right)} \left( e^{g(k,z)}- 1\right), \end{aligned} \end{align*} $$
where
 $$ \begin{align*}g(k,z)=\frac{\pi^2 e^{-2\pi \frac{1}{k} \mathrm{Re}(\frac{1}{z})}}{6(1-e^{-2\pi \frac{1}{k} \mathrm{Re}(\frac{1}{z})})} + \frac{\pi^2 e^{-2\pi \frac{9}{k} \mathrm{Re}(\frac{1}{z})}}{6(1-e^{-2\pi \frac{9}{k} \mathrm{Re}(\frac{1}{z})})} + \frac{3\pi^2 e^{-2\pi \frac{3}{k} \mathrm{Re}(\frac{1}{z})}}{6(1-e^{-2\pi \frac{3}{k} \mathrm{Re}(\frac{1}{z})})}.\end{align*} $$
$$ \begin{align*}g(k,z)=\frac{\pi^2 e^{-2\pi \frac{1}{k} \mathrm{Re}(\frac{1}{z})}}{6(1-e^{-2\pi \frac{1}{k} \mathrm{Re}(\frac{1}{z})})} + \frac{\pi^2 e^{-2\pi \frac{9}{k} \mathrm{Re}(\frac{1}{z})}}{6(1-e^{-2\pi \frac{9}{k} \mathrm{Re}(\frac{1}{z})})} + \frac{3\pi^2 e^{-2\pi \frac{3}{k} \mathrm{Re}(\frac{1}{z})}}{6(1-e^{-2\pi \frac{3}{k} \mathrm{Re}(\frac{1}{z})})}.\end{align*} $$
Let
Then,
 $$ \begin{align*} \begin{aligned} & \left| e^{\frac{\pi}{12k}(\frac{1}{z})} \left(\frac{F(e^{2\pi i \gamma_{(h,9l_2)} (\tau)})F(e^{2\pi i \gamma_{(h,l_2)} (9\tau)})}{F(e^{2\pi i \gamma_{(h,3l_2)} (3\tau)})F(e^{2\pi i \gamma_{(3h,l_2)} (27\tau)})^2} - 1 \right) \right| \\ & \quad\leq \frac{1}{x} \left(\mathrm{exp}\left(\frac{\pi^2 x^{24}}{6(1-x^{24})}+\frac{\pi^2 x^{216}}{6(1-x^{216})}+\frac{3\pi^2 x^{72}}{6(1-x^{72})}\right) - 1\right) =: W_3(x). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} & \left| e^{\frac{\pi}{12k}(\frac{1}{z})} \left(\frac{F(e^{2\pi i \gamma_{(h,9l_2)} (\tau)})F(e^{2\pi i \gamma_{(h,l_2)} (9\tau)})}{F(e^{2\pi i \gamma_{(h,3l_2)} (3\tau)})F(e^{2\pi i \gamma_{(3h,l_2)} (27\tau)})^2} - 1 \right) \right| \\ & \quad\leq \frac{1}{x} \left(\mathrm{exp}\left(\frac{\pi^2 x^{24}}{6(1-x^{24})}+\frac{\pi^2 x^{216}}{6(1-x^{216})}+\frac{3\pi^2 x^{72}}{6(1-x^{72})}\right) - 1\right) =: W_3(x). \end{aligned} \end{align*} $$
By Lemma 2.2 and (2.5), we have
 $$ \begin{align*} \begin{aligned} W_3(x) &\leq W_3(e^{-\frac{\pi}{24}}) = e^{\frac{\pi}{24}} \left(\mathrm{exp}\left(\frac{\pi^2 e^{-\pi}}{6(1-e^{-\pi})}+\frac{\pi^2 e^{-9\pi}}{6(1-e^{-9\pi})} + \frac{\pi^2 e^{-3\pi}}{2(1-e^{-3\pi})}\right) - 1\right) \\ & \leq 0.089. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} W_3(x) &\leq W_3(e^{-\frac{\pi}{24}}) = e^{\frac{\pi}{24}} \left(\mathrm{exp}\left(\frac{\pi^2 e^{-\pi}}{6(1-e^{-\pi})}+\frac{\pi^2 e^{-9\pi}}{6(1-e^{-9\pi})} + \frac{\pi^2 e^{-3\pi}}{2(1-e^{-3\pi})}\right) - 1\right) \\ & \leq 0.089. \end{aligned} \end{align*} $$
Hence,
 $$ \begin{align*} \begin{aligned} |P_2| &\leq 0.0297 \sum_{\substack{1 \leq k \leq N \\ (k,27) = 9}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} \int_{\xi_{h,k}} |z|^{-\frac{1}{2}} e^{\frac{-\pi}{12k}\mathrm{Re}(z)} e^{2\pi n \varrho} d\varphi \\ &\leq 0.0297 \sum_{\substack{1 \leq k \leq N \\ (k,27) = 9}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} \int_{\xi_{h,k}} k^{-\frac{1}{2}} N e^{2\pi (n - 1/24) \varrho} d\varphi \\ &\leq 0.0594 \sum_{\substack{1 \leq k \leq N \\ (k,27) = 9}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} k^{-\frac{3}{2}} e^{2\pi (n - 1/24) \varrho} \\ &\leq 0.0594 \sum_{\substack{1 \leq k \leq N \\ (k,27) = 9}} k^{-\frac{1}{2}} e^{2\pi (n - 1/24) \varrho} \\&\leq 0.119 e^{2\pi (n - 1/24) \varrho} N^{\frac{1}{2}}.\\ \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} |P_2| &\leq 0.0297 \sum_{\substack{1 \leq k \leq N \\ (k,27) = 9}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} \int_{\xi_{h,k}} |z|^{-\frac{1}{2}} e^{\frac{-\pi}{12k}\mathrm{Re}(z)} e^{2\pi n \varrho} d\varphi \\ &\leq 0.0297 \sum_{\substack{1 \leq k \leq N \\ (k,27) = 9}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} \int_{\xi_{h,k}} k^{-\frac{1}{2}} N e^{2\pi (n - 1/24) \varrho} d\varphi \\ &\leq 0.0594 \sum_{\substack{1 \leq k \leq N \\ (k,27) = 9}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} k^{-\frac{3}{2}} e^{2\pi (n - 1/24) \varrho} \\ &\leq 0.0594 \sum_{\substack{1 \leq k \leq N \\ (k,27) = 9}} k^{-\frac{1}{2}} e^{2\pi (n - 1/24) \varrho} \\&\leq 0.119 e^{2\pi (n - 1/24) \varrho} N^{\frac{1}{2}}.\\ \end{aligned} \end{align*} $$
For
![]() $P_1,$
applying Lemma 2.3 with
$P_1,$
applying Lemma 2.3 with
![]() $b=1$
, we establish
$b=1$
, we establish
 $$ \begin{align*} P_1 &= \frac{1}{3} \sum_{\substack{1 \leq k \leq N \\ (k,27) = 9}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} e^{-2\pi i (n-2)h/k} \Omega_{(h,k)} \int_{\xi_{h,k}} e^{\frac{\pi}{12k}(\frac{1}{z} - z)} z^{-\frac{1}{2}} e^{2\pi n \varrho} e^{-2\pi i n \varphi} d\varphi \notag \\ &=\frac{1}{3} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} e^{-2\pi i (n-2)h/9} \Omega_{(h,9)} \sqrt{\frac{2}{9(n-1/24)}} \mathrm{cosh}\left(\frac{\pi}{9} \sqrt{\frac{2}{3}\left(n-\frac{1}{24}\right)} \right) \notag \\ & \quad+\frac{1}{3} \sum_{\substack{18 \leq k \leq N \\ (k,27) = 9}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} e^{-2\pi i (n-2)h/k} \Omega_{(h,k)} \sqrt{\frac{2}{k(n-1/24)}} \mathrm{cosh}\left(\frac{\pi}{k} \sqrt{\frac{2}{3}\left(n-\frac{1}{24}\right)} \right)\\ &\quad + \frac{1}{3} \sum_{\substack{1 \leq k \leq N \\ (k,27) = 9}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} e^{-2\pi i (n-2)h/k} \Omega_{(h,k)} E^{(1)}(I) \\ &= \frac{1}{3} \bigg(\sum_{\substack{0 \leq h < 9 \\ (h,9) = 1}} e^{-2\pi i (n-2)h/9} \Omega_{(h,9)}\bigg) \sqrt{\frac{2}{9(n-1/24)}} e^{\frac{\pi}{9} \sqrt{\frac{2}{3}(n-\frac{1}{24})}} \notag \\ &\quad + \frac{1}{3} \bigg(\sum_{\substack{0 \leq h < 9 \\ (h,9) = 1}} e^{-2\pi i (n-2)h/9} \Omega_{(h,9)}\bigg) \sqrt{\frac{2}{9(n-1/24)}} e^{-\frac{\pi}{9} \sqrt{\frac{2}{3}(n-\frac{1}{24})}} \notag \\ & \quad+ \frac{1}{3} \sum_{\substack{18 \leq k \leq N \\ (k,27) = 9}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} e^{-2\pi i (n-2)h/k} \Omega_{(h,k)} \sqrt{\frac{2}{k(n-1/24)}} \mathrm{cosh}\left(\frac{\pi}{k} \sqrt{\frac{2}{3}\left(n-\frac{1}{24}\right)} \right) \notag \\ &\quad+ \frac{1}{3} \sum_{\substack{1 \leq k \leq N \\ (k,27) = 9}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} e^{-2\pi i (n-2)h/k} \Omega_{(h,k)} E^{(1)}(I) \notag \\ & =:P(n) + Q \notag \end{align*} $$
$$ \begin{align*} P_1 &= \frac{1}{3} \sum_{\substack{1 \leq k \leq N \\ (k,27) = 9}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} e^{-2\pi i (n-2)h/k} \Omega_{(h,k)} \int_{\xi_{h,k}} e^{\frac{\pi}{12k}(\frac{1}{z} - z)} z^{-\frac{1}{2}} e^{2\pi n \varrho} e^{-2\pi i n \varphi} d\varphi \notag \\ &=\frac{1}{3} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} e^{-2\pi i (n-2)h/9} \Omega_{(h,9)} \sqrt{\frac{2}{9(n-1/24)}} \mathrm{cosh}\left(\frac{\pi}{9} \sqrt{\frac{2}{3}\left(n-\frac{1}{24}\right)} \right) \notag \\ & \quad+\frac{1}{3} \sum_{\substack{18 \leq k \leq N \\ (k,27) = 9}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} e^{-2\pi i (n-2)h/k} \Omega_{(h,k)} \sqrt{\frac{2}{k(n-1/24)}} \mathrm{cosh}\left(\frac{\pi}{k} \sqrt{\frac{2}{3}\left(n-\frac{1}{24}\right)} \right)\\ &\quad + \frac{1}{3} \sum_{\substack{1 \leq k \leq N \\ (k,27) = 9}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} e^{-2\pi i (n-2)h/k} \Omega_{(h,k)} E^{(1)}(I) \\ &= \frac{1}{3} \bigg(\sum_{\substack{0 \leq h < 9 \\ (h,9) = 1}} e^{-2\pi i (n-2)h/9} \Omega_{(h,9)}\bigg) \sqrt{\frac{2}{9(n-1/24)}} e^{\frac{\pi}{9} \sqrt{\frac{2}{3}(n-\frac{1}{24})}} \notag \\ &\quad + \frac{1}{3} \bigg(\sum_{\substack{0 \leq h < 9 \\ (h,9) = 1}} e^{-2\pi i (n-2)h/9} \Omega_{(h,9)}\bigg) \sqrt{\frac{2}{9(n-1/24)}} e^{-\frac{\pi}{9} \sqrt{\frac{2}{3}(n-\frac{1}{24})}} \notag \\ & \quad+ \frac{1}{3} \sum_{\substack{18 \leq k \leq N \\ (k,27) = 9}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} e^{-2\pi i (n-2)h/k} \Omega_{(h,k)} \sqrt{\frac{2}{k(n-1/24)}} \mathrm{cosh}\left(\frac{\pi}{k} \sqrt{\frac{2}{3}\left(n-\frac{1}{24}\right)} \right) \notag \\ &\quad+ \frac{1}{3} \sum_{\substack{1 \leq k \leq N \\ (k,27) = 9}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} e^{-2\pi i (n-2)h/k} \Omega_{(h,k)} E^{(1)}(I) \notag \\ & =:P(n) + Q \notag \end{align*} $$
with
 $$ \begin{align*} P(n) = \bigg(\frac{1}{3} \sum_{\substack{0 \leq h < 9 \\ (h,9) = 1}} e^{-2\pi i (n-2)h/9} \Omega_{(h,9)}\bigg) \sqrt{\frac{2}{9(n-1/24)}} e^{\frac{\pi}{9} \sqrt{\frac{2}{3}(n-\frac{1}{24})}} \end{align*} $$
$$ \begin{align*} P(n) = \bigg(\frac{1}{3} \sum_{\substack{0 \leq h < 9 \\ (h,9) = 1}} e^{-2\pi i (n-2)h/9} \Omega_{(h,9)}\bigg) \sqrt{\frac{2}{9(n-1/24)}} e^{\frac{\pi}{9} \sqrt{\frac{2}{3}(n-\frac{1}{24})}} \end{align*} $$
and
 $$ \begin{align*} \begin{aligned} |Q| \leq & \sum_{\substack{18 \leq k \leq N \\ (k,27) = 9}} \bigg(\frac{1}{3} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} e^{-2\pi i (n-2)h/k} \Omega_{(h,k)}\bigg) \sqrt{\frac{2}{k(n-1/24)}} \\ & \times \left(e^{\frac{\pi}{k} \sqrt{\frac{2}{3}(n-\frac{1}{24})}} + e^{-\frac{\pi}{k} \sqrt{\frac{2}{3}(n-\frac{1}{24})}}\right) + \frac{2\sqrt{2}}{3} + 11.563 (n-1/24)^{(1/4)}\\ \leq & \sum^{\lfloor\sqrt{2\pi(n-1/24)}/9\rfloor}_{2 \leq l_2 \leq N} \frac{\sqrt{k}}{3} \sqrt{\frac{2}{n-1/24}} \left(e^{\frac{\pi}{18} \sqrt{\frac{2}{3}(n-\frac{1}{24})}} + 1\right)\\ & + \frac{2\sqrt{2}}{3} + 11.563 (n-1/24)^{(1/4)} \\ \leq & \left(\frac{\sqrt{2\pi(n-1/24)}}{9}\right)^{\frac{3}{2}} \sqrt{\frac{2}{n-1/24}} \left(e^{\frac{\pi}{18} \sqrt{\frac{2}{3}(n-\frac{1}{24})}} + 1\right) \\ & + \frac{2\sqrt{2}}{3} + 11.563 (n-1/24)^{(1/4)} \\ \leq & 0.208(n-1/24)^{(1/4)} e^{\frac{\pi}{18} \sqrt{\frac{2}{3}(n-\frac{1}{24})}} + 11.771(n-1/24)^{(1/4)} + 0.943. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} |Q| \leq & \sum_{\substack{18 \leq k \leq N \\ (k,27) = 9}} \bigg(\frac{1}{3} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} e^{-2\pi i (n-2)h/k} \Omega_{(h,k)}\bigg) \sqrt{\frac{2}{k(n-1/24)}} \\ & \times \left(e^{\frac{\pi}{k} \sqrt{\frac{2}{3}(n-\frac{1}{24})}} + e^{-\frac{\pi}{k} \sqrt{\frac{2}{3}(n-\frac{1}{24})}}\right) + \frac{2\sqrt{2}}{3} + 11.563 (n-1/24)^{(1/4)}\\ \leq & \sum^{\lfloor\sqrt{2\pi(n-1/24)}/9\rfloor}_{2 \leq l_2 \leq N} \frac{\sqrt{k}}{3} \sqrt{\frac{2}{n-1/24}} \left(e^{\frac{\pi}{18} \sqrt{\frac{2}{3}(n-\frac{1}{24})}} + 1\right)\\ & + \frac{2\sqrt{2}}{3} + 11.563 (n-1/24)^{(1/4)} \\ \leq & \left(\frac{\sqrt{2\pi(n-1/24)}}{9}\right)^{\frac{3}{2}} \sqrt{\frac{2}{n-1/24}} \left(e^{\frac{\pi}{18} \sqrt{\frac{2}{3}(n-\frac{1}{24})}} + 1\right) \\ & + \frac{2\sqrt{2}}{3} + 11.563 (n-1/24)^{(1/4)} \\ \leq & 0.208(n-1/24)^{(1/4)} e^{\frac{\pi}{18} \sqrt{\frac{2}{3}(n-\frac{1}{24})}} + 11.771(n-1/24)^{(1/4)} + 0.943. \end{aligned} \end{align*} $$
Similarly, applying (3.9), we deduce that
with
 $$ \begin{align*} U_{1} = \sum_{\substack{1 \leq k \leq N \\ (k,27) = 27}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} e^{-2\pi i nh/k} \omega^{(3)}_{(h,k)} \int_{\xi_{h,k}} z^{-\frac{1}{2}} e^{\frac{\pi}{12k}(\frac{1}{z} - z)} e^{2\pi n \varrho} e^{-2\pi i n \varphi} d\varphi, \end{align*} $$
$$ \begin{align*} U_{1} = \sum_{\substack{1 \leq k \leq N \\ (k,27) = 27}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} e^{-2\pi i nh/k} \omega^{(3)}_{(h,k)} \int_{\xi_{h,k}} z^{-\frac{1}{2}} e^{\frac{\pi}{12k}(\frac{1}{z} - z)} e^{2\pi n \varrho} e^{-2\pi i n \varphi} d\varphi, \end{align*} $$
and
Here,
![]() $\omega ^{(3)}_{(h,k)} := e^{\pi i (s(h,27l_3) + s(h,l_3) - 3s(h,3l_3))}.$
$\omega ^{(3)}_{(h,k)} := e^{\pi i (s(h,27l_3) + s(h,l_3) - 3s(h,3l_3))}.$
For
![]() $U_1$
, we have
$U_1$
, we have
 $$ \begin{align*} \begin{aligned} |U_1| &= \sum_{\substack{1 \leq k \leq N \\ (k,27) = 27}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} e^{-2\pi i (n)h/k} \omega^{(3)}_{(h,k)} \int_{\xi_{h,k}} z^{-\frac{1}{2}} e^{\frac{\pi}{12k}(\frac{1}{z} - z)} e^{2\pi n \varrho} e^{-2\pi i n \varphi} d\varphi \\ &\leq \bigg|\sum_{\substack{1 \leq k \leq N \\ (k,27) = 27}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} e^{-2\pi i (n)h/k} \omega^{(3)}_{(h,k)} \sqrt{\frac{2}{k(n-1/24)}} \mathrm{cosh}\left(\frac{\pi}{k} \sqrt{\frac{2}{3}\left(n-\frac{1}{24}\right)} \right)\bigg| \\ &\quad + \bigg|\sum_{\substack{1 \leq k \leq N \\ (k,27) = 27}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} e^{-2\pi i (n)h/k} \omega^{(3)}_{(h,k)} E^{(1)}(I)\bigg| \\ &\leq \sum_{\substack{1 \leq k \leq N \\ (k,27) = 27}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} \sqrt{\frac{2}{k(n-1/24)}} (e^{\frac{\pi}{18} \sqrt{\frac{2}{3}(n-\frac{1}{24})}}+1) + 34.698 (n-1/24)^{(1/4)} \\ &\leq \sum^{\lfloor\sqrt{2\pi (n-1/24)}/27 \rfloor}_{l_3=1} \sqrt{\frac{54l_3}{n-1/24}} (e^{\frac{\pi}{18} \sqrt{\frac{2}{3}(n-\frac{1}{24})}}+1) + 34.698 (n-1/24)^{(1/4)} \\ &\leq \left(\frac{\sqrt{2\pi (n-\frac{1}{24})}}{27}\right)^{\frac{3}{2}} \sqrt{\frac{54}{n-1/24}} (e^{\frac{\pi}{18} \sqrt{\frac{2}{3}(n-\frac{1}{24})}}+1) + 34.698 (n-1/24)^{(1/4)} \\& \leq 0.208(n-1/24)^{(1/4)}e^{\frac{\pi}{18} \sqrt{\frac{2}{3}(n-\frac{1}{24})}} + 34.897(n-1/24)^{(1/4)}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} |U_1| &= \sum_{\substack{1 \leq k \leq N \\ (k,27) = 27}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} e^{-2\pi i (n)h/k} \omega^{(3)}_{(h,k)} \int_{\xi_{h,k}} z^{-\frac{1}{2}} e^{\frac{\pi}{12k}(\frac{1}{z} - z)} e^{2\pi n \varrho} e^{-2\pi i n \varphi} d\varphi \\ &\leq \bigg|\sum_{\substack{1 \leq k \leq N \\ (k,27) = 27}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} e^{-2\pi i (n)h/k} \omega^{(3)}_{(h,k)} \sqrt{\frac{2}{k(n-1/24)}} \mathrm{cosh}\left(\frac{\pi}{k} \sqrt{\frac{2}{3}\left(n-\frac{1}{24}\right)} \right)\bigg| \\ &\quad + \bigg|\sum_{\substack{1 \leq k \leq N \\ (k,27) = 27}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} e^{-2\pi i (n)h/k} \omega^{(3)}_{(h,k)} E^{(1)}(I)\bigg| \\ &\leq \sum_{\substack{1 \leq k \leq N \\ (k,27) = 27}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} \sqrt{\frac{2}{k(n-1/24)}} (e^{\frac{\pi}{18} \sqrt{\frac{2}{3}(n-\frac{1}{24})}}+1) + 34.698 (n-1/24)^{(1/4)} \\ &\leq \sum^{\lfloor\sqrt{2\pi (n-1/24)}/27 \rfloor}_{l_3=1} \sqrt{\frac{54l_3}{n-1/24}} (e^{\frac{\pi}{18} \sqrt{\frac{2}{3}(n-\frac{1}{24})}}+1) + 34.698 (n-1/24)^{(1/4)} \\ &\leq \left(\frac{\sqrt{2\pi (n-\frac{1}{24})}}{27}\right)^{\frac{3}{2}} \sqrt{\frac{54}{n-1/24}} (e^{\frac{\pi}{18} \sqrt{\frac{2}{3}(n-\frac{1}{24})}}+1) + 34.698 (n-1/24)^{(1/4)} \\& \leq 0.208(n-1/24)^{(1/4)}e^{\frac{\pi}{18} \sqrt{\frac{2}{3}(n-\frac{1}{24})}} + 34.897(n-1/24)^{(1/4)}. \end{aligned} \end{align*} $$
3.4 Signs of the Fourier coefficients of
 $g(q)-3h(q)$
$g(q)-3h(q)$
It follows from (3.1) and (3.2) that
From (3.3), (3.4) and the results in Subsections 3.2 and 3.3, we derive that
 $$ \begin{align*} \begin{aligned} a(n) - 3b(n)& = S_1(A) + S_2(A) + S_3(A) + S_4(A) - 3(S_1(B) + S_2(B) + S_3(B) + S_4(B)) \\ & = T_1 - 3R_1 + T_2 - 3R_2 + S_2(A) + S_3(A) - 3S_2(B) \\ &\quad - 3P(n) -3P_2 -3Q + U_1 + U_2 - 3S_4(B) \\ &=: -3P(n) + E(n) \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} a(n) - 3b(n)& = S_1(A) + S_2(A) + S_3(A) + S_4(A) - 3(S_1(B) + S_2(B) + S_3(B) + S_4(B)) \\ & = T_1 - 3R_1 + T_2 - 3R_2 + S_2(A) + S_3(A) - 3S_2(B) \\ &\quad - 3P(n) -3P_2 -3Q + U_1 + U_2 - 3S_4(B) \\ &=: -3P(n) + E(n) \end{aligned} \end{align*} $$
with
 $$ \begin{align*} -3P(n) = -\bigg(\sum_{\substack{0 \leq h < 9 \\ (h,9) = 1}} e^{-2\pi i (n-2)h/9} \Omega_{(h,9)}\bigg) \sqrt{\frac{2}{9(n-1/24)}} e^{\frac{\pi}{9} \sqrt{\frac{2}{3}(n-\frac{1}{24})}}. \end{align*} $$
$$ \begin{align*} -3P(n) = -\bigg(\sum_{\substack{0 \leq h < 9 \\ (h,9) = 1}} e^{-2\pi i (n-2)h/9} \Omega_{(h,9)}\bigg) \sqrt{\frac{2}{9(n-1/24)}} e^{\frac{\pi}{9} \sqrt{\frac{2}{3}(n-\frac{1}{24})}}. \end{align*} $$
From Subsctions 3.2 and 3.3, we know that
 $$ \begin{align*} \begin{cases} |T_1 - 3R_1| & \leq \quad 11.225 (n-1/24)^{(1/4)} e^{\frac{\pi}{18} \sqrt{\frac{2}{3}(n-\frac{1}{24})}} + 80.601 (n-1/24)^{(1/4)}, \\ |T_2| & \leq \quad 7.560 \times 10^{10} e^{2\pi (n - 1/24) \varrho} N^{\frac{1}{2}} = 3.254 \times 10^{11}(n-1/24)^{(1/4)}\\ |R_2| & \leq \quad 1.435 \times 10^{13} e^{2\pi i (n - 1/24) \varrho} N^{\frac{1}{2}} = 6.176 \times 10^{13}(n-1/24)^{(1/4)}, \\ |S_2(A)| & \leq \quad \frac{4}{\sqrt{3}} e^{0.969} e^{2\pi(n-\frac{1}{24})\varrho} N^{\frac{1}{2}} = 26.193(n-1/24)^{(1/4)}, \\ |S_3(A)| & \leq \quad 4\sqrt{3} e^{-2.047} e^{2\pi(n-\frac{1}{24})\varrho} N^{\frac{1}{2}}= 3.850(n-1/24)^{(1/4)}, \\ |S_2(B)| & \leq \quad \frac{4}{3\sqrt{3}} e^{1.710} e^{2\pi(n-\frac{1}{24})\varrho} N^{\frac{1}{2}}=18.318(n-1/24)^{(1/4)}, \\ |P_2| & \leq \quad 0.119 e^{2\pi (n - 1/24) \varrho} N^{\frac{1}{2}}=0.513(n-1/24)^{(1/4)}, \\ |Q| & \leq \quad 0.208(n-1/24)^{(1/4)} e^{\frac{\pi}{18} \sqrt{\frac{2}{3}(n-\frac{1}{24})}} + 11.771(n-1/24)^{(1/4)} + 0.943, \\ |U_1| & \leq \quad 0.208(n-1/24)^{(1/4)}e^{(\frac{\pi}{18} \sqrt{\frac{2}{3}(n-\frac{1}{24})})} + 34.897(n-1/24)^{(1/4)}, \\ |U_2| & \leq \quad 0.3536 e^{2\pi (n - 1/24) \varrho} N^{\frac{1}{2}} = 1.522(n-1/24)^{(1/4)}, \\ |S_4(B)| & \leq \quad 4e^{-6.077} e^{2\pi(n-\frac{1}{24})\varrho} N^{\frac{1}{2}}=0.040(n-1/24)^{(1/4)}, \end{cases} \end{align*} $$
$$ \begin{align*} \begin{cases} |T_1 - 3R_1| & \leq \quad 11.225 (n-1/24)^{(1/4)} e^{\frac{\pi}{18} \sqrt{\frac{2}{3}(n-\frac{1}{24})}} + 80.601 (n-1/24)^{(1/4)}, \\ |T_2| & \leq \quad 7.560 \times 10^{10} e^{2\pi (n - 1/24) \varrho} N^{\frac{1}{2}} = 3.254 \times 10^{11}(n-1/24)^{(1/4)}\\ |R_2| & \leq \quad 1.435 \times 10^{13} e^{2\pi i (n - 1/24) \varrho} N^{\frac{1}{2}} = 6.176 \times 10^{13}(n-1/24)^{(1/4)}, \\ |S_2(A)| & \leq \quad \frac{4}{\sqrt{3}} e^{0.969} e^{2\pi(n-\frac{1}{24})\varrho} N^{\frac{1}{2}} = 26.193(n-1/24)^{(1/4)}, \\ |S_3(A)| & \leq \quad 4\sqrt{3} e^{-2.047} e^{2\pi(n-\frac{1}{24})\varrho} N^{\frac{1}{2}}= 3.850(n-1/24)^{(1/4)}, \\ |S_2(B)| & \leq \quad \frac{4}{3\sqrt{3}} e^{1.710} e^{2\pi(n-\frac{1}{24})\varrho} N^{\frac{1}{2}}=18.318(n-1/24)^{(1/4)}, \\ |P_2| & \leq \quad 0.119 e^{2\pi (n - 1/24) \varrho} N^{\frac{1}{2}}=0.513(n-1/24)^{(1/4)}, \\ |Q| & \leq \quad 0.208(n-1/24)^{(1/4)} e^{\frac{\pi}{18} \sqrt{\frac{2}{3}(n-\frac{1}{24})}} + 11.771(n-1/24)^{(1/4)} + 0.943, \\ |U_1| & \leq \quad 0.208(n-1/24)^{(1/4)}e^{(\frac{\pi}{18} \sqrt{\frac{2}{3}(n-\frac{1}{24})})} + 34.897(n-1/24)^{(1/4)}, \\ |U_2| & \leq \quad 0.3536 e^{2\pi (n - 1/24) \varrho} N^{\frac{1}{2}} = 1.522(n-1/24)^{(1/4)}, \\ |S_4(B)| & \leq \quad 4e^{-6.077} e^{2\pi(n-\frac{1}{24})\varrho} N^{\frac{1}{2}}=0.040(n-1/24)^{(1/4)}, \end{cases} \end{align*} $$
so that
 $$ \begin{align*} \begin{aligned} |E(n)| &\leq |T_1 - 3R_1| + |T_2| + 3|R_2| + |S_2(A)| + |S_3(A)| + 3|S_2(B)| \\ &\quad + 3|P_2| + 3|Q| + |U_1| + |U_2| + 3|S_4(B)| \\ &\leq 12.057(n-1/24)^{(1/4)}e^{\frac{\pi}{18} \sqrt{\frac{2}{3}(n-\frac{1}{24})}} + 3.772 \\ &\quad + (3.254 \times 10^{11} + 3\times6.176 \times 10^{13} + 26.193 + 3.850 + 3\times 18.318 + \\ &\qquad 3\times 0.513 + 3\times 12.969 + 12.969 + 1.522 + 3\times 0.040)\bigg(n-\frac{1}{24}\bigg)^{\frac{1}{4}} \\ &\leq 12.057(n-1/24)^{(1/4)}e^{\frac{\pi}{18} \sqrt{\frac{2}{3}(n-\frac{1}{24})}} + 1.857\times 10^{14}\bigg(n-\frac{1}{24}\bigg)^{\frac{1}{4}}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} |E(n)| &\leq |T_1 - 3R_1| + |T_2| + 3|R_2| + |S_2(A)| + |S_3(A)| + 3|S_2(B)| \\ &\quad + 3|P_2| + 3|Q| + |U_1| + |U_2| + 3|S_4(B)| \\ &\leq 12.057(n-1/24)^{(1/4)}e^{\frac{\pi}{18} \sqrt{\frac{2}{3}(n-\frac{1}{24})}} + 3.772 \\ &\quad + (3.254 \times 10^{11} + 3\times6.176 \times 10^{13} + 26.193 + 3.850 + 3\times 18.318 + \\ &\qquad 3\times 0.513 + 3\times 12.969 + 12.969 + 1.522 + 3\times 0.040)\bigg(n-\frac{1}{24}\bigg)^{\frac{1}{4}} \\ &\leq 12.057(n-1/24)^{(1/4)}e^{\frac{\pi}{18} \sqrt{\frac{2}{3}(n-\frac{1}{24})}} + 1.857\times 10^{14}\bigg(n-\frac{1}{24}\bigg)^{\frac{1}{4}}. \end{aligned} \end{align*} $$
It is observed that the signs of the main term
![]() $P(n)$
are determined by
$P(n)$
are determined by
 $$ \begin{align*} \sum_{\substack{0 \leq h < 9 \\ (h,9) = 1}} e^{-2\pi i (n-2)h/9} \Omega_{(h,9)} \end{align*} $$
$$ \begin{align*} \sum_{\substack{0 \leq h < 9 \\ (h,9) = 1}} e^{-2\pi i (n-2)h/9} \Omega_{(h,9)} \end{align*} $$
with
![]() $\Omega _{(h,9)}:= e^{\pi i (s(h,9l_2) + s(h,l_2) - s(h,3l_1) - 2s(3h,l_2))}$
. After calculations, we have
$\Omega _{(h,9)}:= e^{\pi i (s(h,9l_2) + s(h,l_2) - s(h,3l_1) - 2s(3h,l_2))}$
. After calculations, we have
 $$ \begin{align*} \begin{cases} \Omega_{(1,9)} = e^{\frac{25}{54}\pi i},\quad \Omega_{(2,9)} = e^{\frac{11}{54}\pi i}, \\ \Omega_{(4,9)} = e^{-\frac{11}{54}\pi i},\quad \Omega_{(5,9)} = e^{\frac{11}{54}\pi i}, \\ \Omega_{(7,9)} = e^{-\frac{11}{54}\pi i},\quad \Omega_{(8,9)} = e^{-\frac{25}{54}\pi i}. \end{cases} \end{align*} $$
$$ \begin{align*} \begin{cases} \Omega_{(1,9)} = e^{\frac{25}{54}\pi i},\quad \Omega_{(2,9)} = e^{\frac{11}{54}\pi i}, \\ \Omega_{(4,9)} = e^{-\frac{11}{54}\pi i},\quad \Omega_{(5,9)} = e^{\frac{11}{54}\pi i}, \\ \Omega_{(7,9)} = e^{-\frac{11}{54}\pi i},\quad \Omega_{(8,9)} = e^{-\frac{25}{54}\pi i}. \end{cases} \end{align*} $$
Therefore,
 $$ \begin{align*} \sum_{\substack{0 \leq h < 9 \\ (h,9) = 1}} e^{-2\pi i (n-2)h/9} \Omega_{(h,9)} = \begin{cases} 2\mathrm{cos}(23\pi/54) + 4\mathrm{cos}(49\pi/54) & \mathrm{if} ~n \equiv 0 ~(\mathrm{mod} ~ 9) \\ 2\mathrm{cos}(35\pi/54) + 4\mathrm{cos}(37\pi/54) & \mathrm{if} ~n \equiv 1 ~(\mathrm{mod} ~ 9) \\ 2\mathrm{cos}(25\pi/54) + 4\mathrm{cos}(11\pi/54) & \mathrm{if} ~n \equiv 2 ~(\mathrm{mod} ~ 9) \\ 2\mathrm{cos}(49\pi/54) + 4\mathrm{cos}(13\pi/54) & \mathrm{if} ~n \equiv 3 ~(\mathrm{mod} ~ 9) \\ 2\mathrm{cos}(37\pi/54) + 4\mathrm{cos}(\pi/54) & \mathrm{if} ~n \equiv 4 ~(\mathrm{mod} ~ 9) \\ 2\mathrm{cos}(11\pi/54) + 4\mathrm{cos}(47\pi/54) & \mathrm{if} ~n \equiv 5 ~(\mathrm{mod} ~ 9) \\ 2\mathrm{cos}(13\pi/54) + 4\mathrm{cos}(23\pi/54) & \mathrm{if} ~n \equiv 6 ~(\mathrm{mod} ~ 9) \\ 2\mathrm{cos}(\pi/54) + 4\mathrm{cos}(35\pi/54) & \mathrm{if} ~n \equiv 7 ~(\mathrm{mod} ~ 9) \\ 2\mathrm{cos}(47\pi/54) + 4\mathrm{cos}(25\pi/54) & \mathrm{if} ~n \equiv 8 ~(\mathrm{mod} ~ 9). \\ \end{cases} \end{align*} $$
$$ \begin{align*} \sum_{\substack{0 \leq h < 9 \\ (h,9) = 1}} e^{-2\pi i (n-2)h/9} \Omega_{(h,9)} = \begin{cases} 2\mathrm{cos}(23\pi/54) + 4\mathrm{cos}(49\pi/54) & \mathrm{if} ~n \equiv 0 ~(\mathrm{mod} ~ 9) \\ 2\mathrm{cos}(35\pi/54) + 4\mathrm{cos}(37\pi/54) & \mathrm{if} ~n \equiv 1 ~(\mathrm{mod} ~ 9) \\ 2\mathrm{cos}(25\pi/54) + 4\mathrm{cos}(11\pi/54) & \mathrm{if} ~n \equiv 2 ~(\mathrm{mod} ~ 9) \\ 2\mathrm{cos}(49\pi/54) + 4\mathrm{cos}(13\pi/54) & \mathrm{if} ~n \equiv 3 ~(\mathrm{mod} ~ 9) \\ 2\mathrm{cos}(37\pi/54) + 4\mathrm{cos}(\pi/54) & \mathrm{if} ~n \equiv 4 ~(\mathrm{mod} ~ 9) \\ 2\mathrm{cos}(11\pi/54) + 4\mathrm{cos}(47\pi/54) & \mathrm{if} ~n \equiv 5 ~(\mathrm{mod} ~ 9) \\ 2\mathrm{cos}(13\pi/54) + 4\mathrm{cos}(23\pi/54) & \mathrm{if} ~n \equiv 6 ~(\mathrm{mod} ~ 9) \\ 2\mathrm{cos}(\pi/54) + 4\mathrm{cos}(35\pi/54) & \mathrm{if} ~n \equiv 7 ~(\mathrm{mod} ~ 9) \\ 2\mathrm{cos}(47\pi/54) + 4\mathrm{cos}(25\pi/54) & \mathrm{if} ~n \equiv 8 ~(\mathrm{mod} ~ 9). \\ \end{cases} \end{align*} $$
It is easily computed that
 $$ \begin{align*} \bigg|\sum_{\substack{0 \leq h < 9 \\ (h,9) = 1}} e^{-2\pi i (n-2)h/9} \Omega_{(h,9)}\bigg|\geq 0.20142 \end{align*} $$
$$ \begin{align*} \bigg|\sum_{\substack{0 \leq h < 9 \\ (h,9) = 1}} e^{-2\pi i (n-2)h/9} \Omega_{(h,9)}\bigg|\geq 0.20142 \end{align*} $$
for
![]() $n\in \mathbb {N}.$
When
$n\in \mathbb {N}.$
When
![]() $n \geq 22472$
,
$n \geq 22472$
,
 $$ \begin{align*} \begin{aligned} |-3P(n)| &= \bigg|\bigg(\sum_{\substack{0 \leq h < 9 \\ (h,9) = 1}} e^{-2\pi i (n-2)h/9} \Omega_{(h,9)}\bigg) \sqrt{\frac{2}{9(n-1/24)}} e^{\frac{\pi}{9} \sqrt{\frac{2}{3}(n-\frac{1}{24})}}\bigg| \\ & \geq 0.20142 \sqrt{\frac{2}{9(n-1/24)}} e^{\frac{\pi}{9} \sqrt{\frac{2}{3}(n-\frac{1}{24})}} \\ &> 12.057(n-1/24)^{(1/4)}e^{\frac{\pi}{18} \sqrt{\frac{2}{3}(n-\frac{1}{24})}} + 1.857\times 10^{14}\bigg(n-\frac{1}{24}\bigg)^{\frac{1}{4}}\\ & \geq |E(n)|. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} |-3P(n)| &= \bigg|\bigg(\sum_{\substack{0 \leq h < 9 \\ (h,9) = 1}} e^{-2\pi i (n-2)h/9} \Omega_{(h,9)}\bigg) \sqrt{\frac{2}{9(n-1/24)}} e^{\frac{\pi}{9} \sqrt{\frac{2}{3}(n-\frac{1}{24})}}\bigg| \\ & \geq 0.20142 \sqrt{\frac{2}{9(n-1/24)}} e^{\frac{\pi}{9} \sqrt{\frac{2}{3}(n-\frac{1}{24})}} \\ &> 12.057(n-1/24)^{(1/4)}e^{\frac{\pi}{18} \sqrt{\frac{2}{3}(n-\frac{1}{24})}} + 1.857\times 10^{14}\bigg(n-\frac{1}{24}\bigg)^{\frac{1}{4}}\\ & \geq |E(n)|. \end{aligned} \end{align*} $$
From this, we obtain that
 $$ \begin{align} \begin{cases} a(n) - 3b(n)> 0 & \mathrm{if} ~ n \equiv 0,1,5,8 ~ (\mathrm{mod}~9) \\ a(n) - 3b(n) < 0 & \mathrm{if} ~ n \equiv 2,3,4,6,7 ~ (\mathrm{mod}~9) \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} a(n) - 3b(n)> 0 & \mathrm{if} ~ n \equiv 0,1,5,8 ~ (\mathrm{mod}~9) \\ a(n) - 3b(n) < 0 & \mathrm{if} ~ n \equiv 2,3,4,6,7 ~ (\mathrm{mod}~9) \end{cases} \end{align} $$
holds for
![]() $n\geq 22472$
. Calculating the first
$n\geq 22472$
. Calculating the first
![]() $22471$
coefficients of
$22471$
coefficients of
![]() $g(q)-3h(q)$
by using the software Mathematica, we find that (3.11) is also true for
$g(q)-3h(q)$
by using the software Mathematica, we find that (3.11) is also true for
![]() $467 \leq n \leq 22471.$
$467 \leq n \leq 22471.$
3.5 Proof of Theorem 1.1
It follows from the identities in [Reference Aygin and Chan6, eqs.(2.10) and (2.11)] that
and
so that
 $$ \begin{align*} \begin{aligned} M(0,1,1;9;n) - \frac{p(n)}{3} &= \frac{2}{3}(a(n) - 3b(n) ), \\ M(2,3,4;9;n) - \frac{p(n)}{3} &= -\frac{1}{3}(a(n) - 3b(n) ). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} M(0,1,1;9;n) - \frac{p(n)}{3} &= \frac{2}{3}(a(n) - 3b(n) ), \\ M(2,3,4;9;n) - \frac{p(n)}{3} &= -\frac{1}{3}(a(n) - 3b(n) ). \end{aligned} \end{align*} $$
It is known from Subsection 3.4 that (3.11) holds for
![]() $n \geq 467.$
Hence, when
$n \geq 467.$
Hence, when
![]() $n \geq 467,$
$n \geq 467,$
 $$ \begin{align*} \begin{cases} M(0,1,1;9;n)> \frac{p(n)}{3}, & \mathrm{if} ~ n \equiv 0,1,5,8 ~ (\mathrm{mod}~9), \\[1ex] M(0,1,1;9;n) < \frac{p(n)}{3}, & \mathrm{if} ~ n \equiv 2,3,4,6,7 ~ (\mathrm{mod}~9), \\[1ex] M(2,3,4;9;n) < \frac{p(n)}{3}, & \mathrm{if} ~ n \equiv 0,1,5,8 ~ (\mathrm{mod}~9), \\[1ex] M(2,3,4;9;n)> \frac{p(n)}{3}, & \mathrm{if} ~ n \equiv 2,3,4,6,7 ~ (\mathrm{mod}~9). \\[1ex] \end{cases} \end{align*} $$
$$ \begin{align*} \begin{cases} M(0,1,1;9;n)> \frac{p(n)}{3}, & \mathrm{if} ~ n \equiv 0,1,5,8 ~ (\mathrm{mod}~9), \\[1ex] M(0,1,1;9;n) < \frac{p(n)}{3}, & \mathrm{if} ~ n \equiv 2,3,4,6,7 ~ (\mathrm{mod}~9), \\[1ex] M(2,3,4;9;n) < \frac{p(n)}{3}, & \mathrm{if} ~ n \equiv 0,1,5,8 ~ (\mathrm{mod}~9), \\[1ex] M(2,3,4;9;n)> \frac{p(n)}{3}, & \mathrm{if} ~ n \equiv 2,3,4,6,7 ~ (\mathrm{mod}~9). \\[1ex] \end{cases} \end{align*} $$
This finishes the proof of Theorem 1.1.
Acknowledgements
The authors would like to thank the referee for his/her meticulously thorough reading of this paper and for numerous helpful comments and suggestions which greatly improved the exposition of this paper. This work was partially supported by the Natural Science Foundation of Changsha (Grant No. kq2208251).