No CrossRef data available.
Published online by Cambridge University Press: 20 November 2018
Let 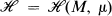 denote the group of all homeomorphisms of a σ-compact manifold which preserve a σ-finite, nonatomic, locally positive and locally finite measure μ. In two recent papers [4, 5] the possible ergodicity of a homeomorphism h in
denote the group of all homeomorphisms of a σ-compact manifold which preserve a σ-finite, nonatomic, locally positive and locally finite measure μ. In two recent papers [4, 5] the possible ergodicity of a homeomorphism h in 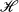 was shown to be related to the homeomorphism h* induced by h on the ends of M. An end of a manifold is, roughly speaking, a distinct way of going to infinity. Those papers demonstrated in particular that
was shown to be related to the homeomorphism h* induced by h on the ends of M. An end of a manifold is, roughly speaking, a distinct way of going to infinity. Those papers demonstrated in particular that 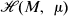 always contains an ergodic homeomorphism, paralleling the similar result of Oxtoby and Ulam [11] for compact manifolds with finite measures. Unfortunately the techniques used in [4] and [5] rely on the fact that a skyscraper construction with an ergodic base transformation is ergodic, a result which cannot be extended to finer properties than ergodicity.
always contains an ergodic homeomorphism, paralleling the similar result of Oxtoby and Ulam [11] for compact manifolds with finite measures. Unfortunately the techniques used in [4] and [5] rely on the fact that a skyscraper construction with an ergodic base transformation is ergodic, a result which cannot be extended to finer properties than ergodicity.