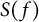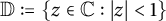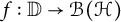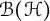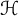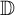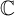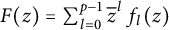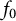1 Introduction
Let
![]() $H^{\infty }(\mathbb {D})$
be the space of bounded analytic functions from the unit disk
$H^{\infty }(\mathbb {D})$
be the space of bounded analytic functions from the unit disk
![]() $\mathbb {D}:=\{z \in \mathbb {C}:|z|<1\}$
into the complex plane
$\mathbb {D}:=\{z \in \mathbb {C}:|z|<1\}$
into the complex plane
![]() $\mathbb {C}$
and denote
$\mathbb {C}$
and denote
![]() $\left \lVert f\right \rVert _{\infty }:=\sup _{|z|<1} |f(z)|$
. In
$\left \lVert f\right \rVert _{\infty }:=\sup _{|z|<1} |f(z)|$
. In
![]() $1914$
, the following remarkable result for the universal constant
$1914$
, the following remarkable result for the universal constant
![]() $r=1/3$
for functions in
$r=1/3$
for functions in
![]() $H^{\infty }(\mathbb {D})$
was proved by Bohr [Reference Bohr13].
$H^{\infty }(\mathbb {D})$
was proved by Bohr [Reference Bohr13].
Theorem A Let
![]() $f \in H^{\infty }(\mathbb {D})$
with the power series
$f \in H^{\infty }(\mathbb {D})$
with the power series
![]() $f(z)=\sum _{n=0}^{\infty } a_{n}z^{n}$
. Then
$f(z)=\sum _{n=0}^{\infty } a_{n}z^{n}$
. Then
 $$ \begin{align} \sum_{n=0}^{\infty} |a_{n}|r^{n} \leq \left\lVert f\right\rVert_{\infty} \end{align} $$
$$ \begin{align} \sum_{n=0}^{\infty} |a_{n}|r^{n} \leq \left\lVert f\right\rVert_{\infty} \end{align} $$
for
![]() $|z|=r \leq 1/3$
, and the constant
$|z|=r \leq 1/3$
, and the constant
![]() $1/3$
, referred to as the classical Bohr radius, is the best possible.
$1/3$
, referred to as the classical Bohr radius, is the best possible.
The interest in the Bohr inequality has been revived when Dixon [Reference Dixon15] used it to disprove the conjecture that if the nonunital von Neumann’s inequality holds for a Banach algebra, then it is necessarily an operator algebra. In
![]() $2004$
, Paulsen and Singh [Reference Paulsen and Singh22] extended Bohr’s theorem to Banach algebras by finding a general version of Bohr inequality which is valid in the context of uniform algebras. For fixed
$2004$
, Paulsen and Singh [Reference Paulsen and Singh22] extended Bohr’s theorem to Banach algebras by finding a general version of Bohr inequality which is valid in the context of uniform algebras. For fixed
![]() $z\in \mathbb {D}$
, we denote
$z\in \mathbb {D}$
, we denote
 $$ \begin{align*} \mathcal{G}_{z}:= \left\{f(z)=\sum_{n=0}^{\infty} a_{n}z^n: f\in H^{\infty}(\mathbb{D}) \right\}. \end{align*} $$
$$ \begin{align*} \mathcal{G}_{z}:= \left\{f(z)=\sum_{n=0}^{\infty} a_{n}z^n: f\in H^{\infty}(\mathbb{D}) \right\}. \end{align*} $$
For
![]() $|z|=r$
, the Bohr operator
$|z|=r$
, the Bohr operator
![]() $M_{r}$
on
$M_{r}$
on
![]() $\mathcal {G}_{z}$
is defined by
$\mathcal {G}_{z}$
is defined by
 $$ \begin{align*} M_{r}(f)= \sum_{n=0}^{\infty} |a_{n}| |z^n|= \sum_{n=0}^{\infty} |a_{n}| r^n. \end{align*} $$
$$ \begin{align*} M_{r}(f)= \sum_{n=0}^{\infty} |a_{n}| |z^n|= \sum_{n=0}^{\infty} |a_{n}| r^n. \end{align*} $$
The Bohr operator has the following properties, which has been established in [Reference Paulsen and Singh23].
Theorem 1.1 [Reference Abu Muhanna, Ali, Ng and Lee2]
For each fixed
![]() $z \in \mathbb {D}$
and
$z \in \mathbb {D}$
and
![]() $|z|=r$
, the Bohr operator
$|z|=r$
, the Bohr operator
![]() $M_{r}$
satisfies:
$M_{r}$
satisfies:
-
(1)
 $M_{r}(f) \geq 0$
, and
$M_{r}(f) \geq 0$
, and
 $M_{r}(f)=0$
if, and only if,
$M_{r}(f)=0$
if, and only if,
 $f\equiv 0$
,
$f\equiv 0$
, -
(2)
 $M_{r}(f+g) \leq M_{r}(f)+M_{r}(g)$
,
$M_{r}(f+g) \leq M_{r}(f)+M_{r}(g)$
, -
(3)
 $M_{r}(\alpha f)= |\alpha | M_{r}(f)$
,
$M_{r}(\alpha f)= |\alpha | M_{r}(f)$
,
 $\alpha \in \mathbb {C}$
,
$\alpha \in \mathbb {C}$
, -
(4)
 $M_{r}(f.g)\leq M_{r}(f).M_{r}(g)$
,
$M_{r}(f.g)\leq M_{r}(f).M_{r}(g)$
, -
(5)
 $M_{r}(1)=1$
.
$M_{r}(1)=1$
.
By the virtue of Theorem 1.1, it is worth to mention that the space
![]() $\mathcal {G}_{z}$
with the norm
$\mathcal {G}_{z}$
with the norm
![]() $M_{r}$
constitutes a Banach algebra. However, not all Banach spaces satisfy the Bohr phenomenon. In [Reference BÉnÉteau, Dahlner and Khavinson7], Bénéteau et al. have shown that
$M_{r}$
constitutes a Banach algebra. However, not all Banach spaces satisfy the Bohr phenomenon. In [Reference BÉnÉteau, Dahlner and Khavinson7], Bénéteau et al. have shown that
![]() $H^{q}$
, the usual Hardy spaces in
$H^{q}$
, the usual Hardy spaces in
![]() $\mathbb {D}$
, do not satisfy the Bohr phenomenon for any
$\mathbb {D}$
, do not satisfy the Bohr phenomenon for any
![]() $0<q<\infty $
. A complex Banach algebra
$0<q<\infty $
. A complex Banach algebra
![]() $\mathcal {A}$
satisfies the von Neumann inequality if for all polynomial
$\mathcal {A}$
satisfies the von Neumann inequality if for all polynomial
![]() $p(X)$
and for all
$p(X)$
and for all
![]() $x \in \mathcal {A}$
with
$x \in \mathcal {A}$
with
![]() $\left \lVert x\right \rVert \leq 1$
,
$\left \lVert x\right \rVert \leq 1$
,
In [Reference von Neumann25], von Neumann has shown that the algebra
![]() $\mathcal {B}(\mathcal {H})$
of all bounded operators on a Hilbert space
$\mathcal {B}(\mathcal {H})$
of all bounded operators on a Hilbert space
![]() $\mathcal {H}$
satisfies the inequality (1.2). It is well known that every Banach algebra which is an operator algebra (i.e., which is isometrically isomorphic to a closed subalgebra of
$\mathcal {H}$
satisfies the inequality (1.2). It is well known that every Banach algebra which is an operator algebra (i.e., which is isometrically isomorphic to a closed subalgebra of
![]() $\mathcal {B}(\mathcal {H})$
for some Hilbert space
$\mathcal {B}(\mathcal {H})$
for some Hilbert space
![]() $\mathcal {H}$
) also satisfies the von Neumann inequality (1.2). Bohr inequality has been extended to several complex variables and more abstract settings (see [Reference Aytuna and Djakov8, Reference Boas and Khavinson12, Reference Defant, García, Maestre and Pérez-García14, Reference Hamada, Honda and Kohr19, Reference Paulsen, Popescu and Singh21, Reference Paulsen and Singh22, Reference Popescu24]).
$\mathcal {H}$
) also satisfies the von Neumann inequality (1.2). Bohr inequality has been extended to several complex variables and more abstract settings (see [Reference Aytuna and Djakov8, Reference Boas and Khavinson12, Reference Defant, García, Maestre and Pérez-García14, Reference Hamada, Honda and Kohr19, Reference Paulsen, Popescu and Singh21, Reference Paulsen and Singh22, Reference Popescu24]).
Another interesting aspect of Bohr phenomenon thrives on considering the Bohr radius problem for subordinating families of analytic functions in
![]() $\mathbb {D}$
. For two analytic functions g and f in
$\mathbb {D}$
. For two analytic functions g and f in
![]() $\mathbb {D}$
, we say that g is subordinate to f, written
$\mathbb {D}$
, we say that g is subordinate to f, written
![]() $g \prec f$
, if there exists an analytic function
$g \prec f$
, if there exists an analytic function
![]() $\phi :\mathbb {D} \rightarrow \mathbb {D}$
with
$\phi :\mathbb {D} \rightarrow \mathbb {D}$
with
![]() $\phi (0)=0$
such that
$\phi (0)=0$
such that
![]() $g(z)=f(\phi (z))$
in
$g(z)=f(\phi (z))$
in
![]() $\mathbb {D}$
. Let
$\mathbb {D}$
. Let
![]() $S(f)$
be the class of analytic functions subordinate to f in
$S(f)$
be the class of analytic functions subordinate to f in
![]() $\mathbb {D}$
. We say that g is quasi-subordinate to f if there exists an analytic function
$\mathbb {D}$
. We say that g is quasi-subordinate to f if there exists an analytic function
![]() $\psi $
with
$\psi $
with
![]() $|\psi (z)|\leq 1$
in
$|\psi (z)|\leq 1$
in
![]() $\mathbb {D}$
such that
$\mathbb {D}$
such that
![]() $g(z)=\psi (z)f(\phi (z))$
in
$g(z)=\psi (z)f(\phi (z))$
in
![]() $\mathbb {D}$
. It is well known that if g is subordinate (or quasi-subordinate) to f in
$\mathbb {D}$
. It is well known that if g is subordinate (or quasi-subordinate) to f in
![]() $\mathbb {D}$
, then
$\mathbb {D}$
, then
![]() $M_{r}(g) \leq M_{r}(f)$
for
$M_{r}(g) \leq M_{r}(f)$
for
![]() $|z|=r \leq 1/3$
. Bhowmik and Das [Reference Bhowmik and Das10] have studied the Bohr radius for the subordinating families, and the Bohr radius for quasi-subordination families has been studied by Alkhaleefah et al. [Reference Alkhaleefah, Kayumov and Ponnusamy5]. In
$|z|=r \leq 1/3$
. Bhowmik and Das [Reference Bhowmik and Das10] have studied the Bohr radius for the subordinating families, and the Bohr radius for quasi-subordination families has been studied by Alkhaleefah et al. [Reference Alkhaleefah, Kayumov and Ponnusamy5]. In
![]() $2021$
, Bhowmik and Das [Reference Bhowmik and Das11] extended the Bohr phenomenon for the subordination to operator-valued analytic functions in
$2021$
, Bhowmik and Das [Reference Bhowmik and Das11] extended the Bohr phenomenon for the subordination to operator-valued analytic functions in
![]() $\mathbb {D}$
. Throughout this article,
$\mathbb {D}$
. Throughout this article,
![]() $\mathcal {B}(\mathcal {H})$
stands for the space of bounded linear operators on a complex Hilbert space
$\mathcal {B}(\mathcal {H})$
stands for the space of bounded linear operators on a complex Hilbert space
![]() $\mathcal {H}$
. We want to concentrate operator-valued holomorphic functions
$\mathcal {H}$
. We want to concentrate operator-valued holomorphic functions
![]() $f:\mathbb {D} \rightarrow \mathcal {B}(\mathcal {H})$
. The term subordination for operator-valued functions can be defined as the scalar valued case. That is, for two holomorphic functions
$f:\mathbb {D} \rightarrow \mathcal {B}(\mathcal {H})$
. The term subordination for operator-valued functions can be defined as the scalar valued case. That is, for two holomorphic functions
![]() $g,f:\mathbb {D} \rightarrow \mathcal {B}(\mathcal {H})$
, we say that g is subordinate to f, written
$g,f:\mathbb {D} \rightarrow \mathcal {B}(\mathcal {H})$
, we say that g is subordinate to f, written
![]() $g \prec f$
, if there exists a holomorphic function
$g \prec f$
, if there exists a holomorphic function
![]() $\phi :\mathbb {D} \rightarrow \mathbb {D}$
with
$\phi :\mathbb {D} \rightarrow \mathbb {D}$
with
![]() $\phi (0)=0$
such that
$\phi (0)=0$
such that
![]() $g(z)=f(\phi (z))$
in
$g(z)=f(\phi (z))$
in
![]() $\mathbb {D}$
. Let
$\mathbb {D}$
. Let
![]() $S(f)$
be the class of analytic functions subordinate to f in
$S(f)$
be the class of analytic functions subordinate to f in
![]() $\mathbb {D}$
. For given two Banach spaces X and Y and a domain
$\mathbb {D}$
. For given two Banach spaces X and Y and a domain
![]() $\Omega \subset X$
, a holomorphic function
$\Omega \subset X$
, a holomorphic function
![]() $f :\Omega \rightarrow Y$
is said to be biholomorphic on
$f :\Omega \rightarrow Y$
is said to be biholomorphic on
![]() $\Omega $
if
$\Omega $
if
![]() $f^{-1}$
exists and is holomorphic in
$f^{-1}$
exists and is holomorphic in
![]() $f(\Omega ) \subseteq Y$
. We say that a biholomorphic function f is starlike in its domain
$f(\Omega ) \subseteq Y$
. We say that a biholomorphic function f is starlike in its domain
![]() $\Omega $
with respect to
$\Omega $
with respect to
![]() $\xi _{0} \in \Omega $
if
$\xi _{0} \in \Omega $
if
![]() $f(\Omega )$
is a starlike domain with respect to
$f(\Omega )$
is a starlike domain with respect to
![]() $f(\xi _{0})$
, i.e.,
$f(\xi _{0})$
, i.e.,
![]() $(1-t) f(\xi _{0}) + tf(z) \in f(\Omega )$
for all
$(1-t) f(\xi _{0}) + tf(z) \in f(\Omega )$
for all
![]() $z \in \Omega $
and
$z \in \Omega $
and
![]() $t \in [0,1]$
. A biholomorphic function f is called starlike if f is starlike with respect to
$t \in [0,1]$
. A biholomorphic function f is called starlike if f is starlike with respect to
![]() $0\in \Omega $
and
$0\in \Omega $
and
![]() $f(0)=0$
. A biholomorphic function f is said to be convex if f is starlike with respect to every point in
$f(0)=0$
. A biholomorphic function f is said to be convex if f is starlike with respect to every point in
![]() $\Omega $
. For convex or star-like biholomorphic function f in
$\Omega $
. For convex or star-like biholomorphic function f in
![]() $\mathbb {D}$
, Bohr phenomenon for any
$\mathbb {D}$
, Bohr phenomenon for any
![]() $g \in S(f)$
has been studied in [Reference Bhowmik and Das11].
$g \in S(f)$
has been studied in [Reference Bhowmik and Das11].
For the rest of our discussion, we introduce some notations. Throughout this paper,
![]() $\left \lVert A\right \rVert $
stands for the operator norm of A for any
$\left \lVert A\right \rVert $
stands for the operator norm of A for any
![]() $A\in \mathcal {B}(\mathcal {H})$
and
$A\in \mathcal {B}(\mathcal {H})$
and
![]() $\left \lvert A\right \rvert =(A^{*}A)^{1/2}$
denotes the absolute value of A, where
$\left \lvert A\right \rvert =(A^{*}A)^{1/2}$
denotes the absolute value of A, where
![]() $A^{*}$
is the adjoint of A and
$A^{*}$
is the adjoint of A and
![]() $T^{1/2}$
denotes the unique positive square root of a positive operator T. We denote I be the identity operator on
$T^{1/2}$
denotes the unique positive square root of a positive operator T. We denote I be the identity operator on
![]() $\mathcal {H}$
.
$\mathcal {H}$
.
In
![]() $2010$
, Fournier and Ruscheweyh [Reference Fournier and Ruscheweyh16] extensively studied the Bohr radius problem for arbitrary simply connected domains containing
$2010$
, Fournier and Ruscheweyh [Reference Fournier and Ruscheweyh16] extensively studied the Bohr radius problem for arbitrary simply connected domains containing
![]() $\mathbb {D}$
. Let
$\mathbb {D}$
. Let
![]() $\mathcal {H}(\Omega )$
be the class of analytic functions
$\mathcal {H}(\Omega )$
be the class of analytic functions
![]() $f : \Omega \rightarrow \mathbb {C}$
, and let
$f : \Omega \rightarrow \mathbb {C}$
, and let
![]() $\mathcal {B}(\Omega )$
denote the class of functions
$\mathcal {B}(\Omega )$
denote the class of functions
![]() $f \in \mathcal {H}(\Omega )$
such that
$f \in \mathcal {H}(\Omega )$
such that
![]() $f(\Omega ) \subseteq \overline {\mathbb {D}}$
. For the class
$f(\Omega ) \subseteq \overline {\mathbb {D}}$
. For the class
![]() $\mathcal {B}(\Omega )$
, the Bohr radius
$\mathcal {B}(\Omega )$
, the Bohr radius
![]() $\mathcal {B}_{\Omega }$
is defined by (see [Reference Ahamed, Allu and Halder4, Reference Fournier and Ruscheweyh16])
$\mathcal {B}_{\Omega }$
is defined by (see [Reference Ahamed, Allu and Halder4, Reference Fournier and Ruscheweyh16])
 $$\begin{align*}B_{\Omega}:=\sup\bigg\{r\in (0,1) : M_{r}(f)\leq 1\; \text{for all}\; f(z)=\sum_{n=0}^{\infty}a_nz^n\in\mathcal{B}(\Omega),\; z\in\mathbb{D}\bigg\}, \end{align*}$$
$$\begin{align*}B_{\Omega}:=\sup\bigg\{r\in (0,1) : M_{r}(f)\leq 1\; \text{for all}\; f(z)=\sum_{n=0}^{\infty}a_nz^n\in\mathcal{B}(\Omega),\; z\in\mathbb{D}\bigg\}, \end{align*}$$
where
![]() $M_{r}(f):=\sum _{n=0}^{\infty }|a_n|r^n$
is the Bohr operator for
$M_{r}(f):=\sum _{n=0}^{\infty }|a_n|r^n$
is the Bohr operator for
![]() $f \in \mathcal {B}(\Omega )$
in
$f \in \mathcal {B}(\Omega )$
in
![]() $\mathbb {D}$
. For
$\mathbb {D}$
. For
![]() $\Omega =\mathbb {D}$
,
$\Omega =\mathbb {D}$
,
![]() $\mathcal {B}(\Omega )$
reduces to
$\mathcal {B}(\Omega )$
reduces to
![]() $B_{\mathbb {D}}=1/3$
, which is the classical Bohr radius for the class
$B_{\mathbb {D}}=1/3$
, which is the classical Bohr radius for the class
![]() $\mathcal {B}(\mathbb {D})$
.
$\mathcal {B}(\mathbb {D})$
.
For
![]() $0\leq \gamma <1$
, Fournier and Ruscheweyh [Reference Fournier and Ruscheweyh16] have estimated the Bohr radius for the class
$0\leq \gamma <1$
, Fournier and Ruscheweyh [Reference Fournier and Ruscheweyh16] have estimated the Bohr radius for the class
![]() $\mathcal {B}(\Omega _{\gamma })$
and proved that
$\mathcal {B}(\Omega _{\gamma })$
and proved that
![]() $\mathcal {B}_{\Omega _{\gamma }}=(1+\gamma )/(3+\gamma )$
, where
$\mathcal {B}_{\Omega _{\gamma }}=(1+\gamma )/(3+\gamma )$
, where
 $$\begin{align*}\Omega_{\gamma}:=\bigg\{z\in\mathbb{C} : \bigg|z+\frac{\gamma}{1-\gamma}\bigg|<\frac{1}{1-\gamma}\bigg\}. \end{align*}$$
$$\begin{align*}\Omega_{\gamma}:=\bigg\{z\in\mathbb{C} : \bigg|z+\frac{\gamma}{1-\gamma}\bigg|<\frac{1}{1-\gamma}\bigg\}. \end{align*}$$
Let
![]() $H^{\infty }(\Omega ,X)$
be the space of bounded analytic functions from
$H^{\infty }(\Omega ,X)$
be the space of bounded analytic functions from
![]() $\Omega $
into a complex Banach space X and
$\Omega $
into a complex Banach space X and
![]() $\left \lVert f\right \rVert _{H^{\infty }(\Omega ,X)}= \sup _{z \in \Omega } \left \lVert f(z)\right \rVert $
. The Bohr phenomenon for operator-valued functions on simply connected domains has been studied in [Reference Allu and Halder6]. Let
$\left \lVert f\right \rVert _{H^{\infty }(\Omega ,X)}= \sup _{z \in \Omega } \left \lVert f(z)\right \rVert $
. The Bohr phenomenon for operator-valued functions on simply connected domains has been studied in [Reference Allu and Halder6]. Let
![]() $\mathcal {B}(\mathcal {H})$
be the algebra of all bounded linear operators on a complex Hilbert space
$\mathcal {B}(\mathcal {H})$
be the algebra of all bounded linear operators on a complex Hilbert space
![]() $\mathcal {H}$
. For the class
$\mathcal {H}$
. For the class
![]() $H^{\infty }(\Omega ,\mathcal {B}(\mathcal {H}))$
, we denote (see [Reference Allu and Halder6])
$H^{\infty }(\Omega ,\mathcal {B}(\mathcal {H}))$
, we denote (see [Reference Allu and Halder6])
 $$ \begin{align} \lambda_{\mathcal{H}}:=\lambda_{\mathcal{H}}(\Omega):= \sup \limits _{\substack{f \in H^{\infty}(\Omega,\mathcal{B}(\mathcal{H}))\\{\left\lVert f(z)\right\rVert\leq1}}} \left\{\frac{\left\lVert A_{n}\right\rVert}{\left\lVert\, I- |A_{0}|^2\right\rVert\,} : A_{0} \not \equiv f(z)= \sum \limits_{n=0}^{\infty} A_{n} z^n, \,\, z \in \mathbb{D}\right\}. \end{align} $$
$$ \begin{align} \lambda_{\mathcal{H}}:=\lambda_{\mathcal{H}}(\Omega):= \sup \limits _{\substack{f \in H^{\infty}(\Omega,\mathcal{B}(\mathcal{H}))\\{\left\lVert f(z)\right\rVert\leq1}}} \left\{\frac{\left\lVert A_{n}\right\rVert}{\left\lVert\, I- |A_{0}|^2\right\rVert\,} : A_{0} \not \equiv f(z)= \sum \limits_{n=0}^{\infty} A_{n} z^n, \,\, z \in \mathbb{D}\right\}. \end{align} $$
Recently, Allu and Halder [Reference Allu and Halder6] have established the Bohr theorem for the functions in
![]() $H^{\infty }(\Omega ,\mathcal {B}(\mathcal {H}))$
.
$H^{\infty }(\Omega ,\mathcal {B}(\mathcal {H}))$
.
Theorem 1.2 [Reference Allu and Halder6]
Let
![]() $f \in H^{\infty }(\Omega ,\mathcal {B}(\mathcal {H}))$
with
$f \in H^{\infty }(\Omega ,\mathcal {B}(\mathcal {H}))$
with
![]() $\left \lVert f(z)\right \rVert _{H^{\infty }(\Omega ,\mathcal {B}(\mathcal {H}))} \leq 1$
such that
$\left \lVert f(z)\right \rVert _{H^{\infty }(\Omega ,\mathcal {B}(\mathcal {H}))} \leq 1$
such that
![]() $f(z)= \sum _{n=0}^{\infty } A_{n}z^n$
in
$f(z)= \sum _{n=0}^{\infty } A_{n}z^n$
in
![]() $\mathbb {D}$
, where
$\mathbb {D}$
, where
![]() $A_{0}=\alpha _{0}I$
for
$A_{0}=\alpha _{0}I$
for
![]() $|\alpha _{0}|<1$
and
$|\alpha _{0}|<1$
and
![]() $A_{n} \in \mathcal {B}(\mathcal {H})$
for all
$A_{n} \in \mathcal {B}(\mathcal {H})$
for all
![]() $n \in \mathbb {N} \cup \{0\}$
. Then
$n \in \mathbb {N} \cup \{0\}$
. Then
 $$ \begin{align} \sum_{n=0}^{\infty} \left\lVert A_{n}\right\rVert r^n \leq 1 \,\,\,\,\,\, \mbox{for} \,\,\,\, r \leq \frac{1}{1+2\lambda_{\mathcal{H}}}. \end{align} $$
$$ \begin{align} \sum_{n=0}^{\infty} \left\lVert A_{n}\right\rVert r^n \leq 1 \,\,\,\,\,\, \mbox{for} \,\,\,\, r \leq \frac{1}{1+2\lambda_{\mathcal{H}}}. \end{align} $$
For
![]() $\Omega =\Omega _{\gamma }$
and
$\Omega =\Omega _{\gamma }$
and
![]() $p=1$
in [Reference Allu and Halder6, Corollary 1.52], we have the following result.
$p=1$
in [Reference Allu and Halder6, Corollary 1.52], we have the following result.
Theorem 1.3 [Reference Allu and Halder6]
Let
![]() $f \in H^{\infty }(\Omega _{\gamma },\mathcal {B}(\mathcal {H}))$
with
$f \in H^{\infty }(\Omega _{\gamma },\mathcal {B}(\mathcal {H}))$
with
![]() $\left \lVert f(z)\right \rVert _{H^{\infty }(\Omega _{\gamma },\mathcal {B}(\mathcal {H}))} \leq 1$
such that
$\left \lVert f(z)\right \rVert _{H^{\infty }(\Omega _{\gamma },\mathcal {B}(\mathcal {H}))} \leq 1$
such that
![]() $f(z)= \sum _{n=0}^{\infty } A_{n}z^n$
in
$f(z)= \sum _{n=0}^{\infty } A_{n}z^n$
in
![]() $\mathbb {D}$
, where
$\mathbb {D}$
, where
![]() $A_{0}=\alpha _{0}I$
for
$A_{0}=\alpha _{0}I$
for
![]() $|\alpha _{0}|<1$
and
$|\alpha _{0}|<1$
and
![]() $A_{n} \in \mathcal {B}(\mathcal {H})$
for all
$A_{n} \in \mathcal {B}(\mathcal {H})$
for all
![]() $n \in \mathbb {N} \cup \{0\}$
. Then
$n \in \mathbb {N} \cup \{0\}$
. Then
 $$ \begin{align} \sum_{n=0}^{\infty} \left\lVert A_{n}\right\rVert r^n \leq 1 \,\,\,\,\,\, \mbox{for} \,\,\,\, r \leq \frac{1+\gamma}{3+\gamma}. \end{align} $$
$$ \begin{align} \sum_{n=0}^{\infty} \left\lVert A_{n}\right\rVert r^n \leq 1 \,\,\,\,\,\, \mbox{for} \,\,\,\, r \leq \frac{1+\gamma}{3+\gamma}. \end{align} $$
When
![]() $\Omega _{\gamma }=\mathbb {D}$
, i.e.,
$\Omega _{\gamma }=\mathbb {D}$
, i.e.,
![]() $\gamma =0$
, under the same assumptions as in Theorem 1.3, we have
$\gamma =0$
, under the same assumptions as in Theorem 1.3, we have
 $$ \begin{align} \sum_{n=0}^{\infty} \left\lVert A_{n}\right\rVert r^n \leq 1 \,\,\,\,\,\, \mbox{for} \,\,\,\, r \leq \frac{1}{3}. \end{align} $$
$$ \begin{align} \sum_{n=0}^{\infty} \left\lVert A_{n}\right\rVert r^n \leq 1 \,\,\,\,\,\, \mbox{for} \,\,\,\, r \leq \frac{1}{3}. \end{align} $$
2 Bohr operator on operator-valued subordination classes
In this section, we study subordination results for Bohr operator on operator-valued analytic functions in
![]() $\mathbb {D}$
. Recall that
$\mathbb {D}$
. Recall that
![]() $\mathcal {B}(\mathcal {H})$
be the algebra of all bounded linear operators on a complex Hilbert space
$\mathcal {B}(\mathcal {H})$
be the algebra of all bounded linear operators on a complex Hilbert space
![]() $\mathcal {H}$
. For analytic functions
$\mathcal {H}$
. For analytic functions
![]() $f:\mathbb {D} \rightarrow \mathcal {B}(\mathcal {H})$
with
$f:\mathbb {D} \rightarrow \mathcal {B}(\mathcal {H})$
with
![]() $f(z)= \sum _{n=0}^{\infty } A_{n} z^n$
in
$f(z)= \sum _{n=0}^{\infty } A_{n} z^n$
in
![]() $\mathbb {D}$
and
$\mathbb {D}$
and
![]() $A_{n} \in \mathcal {B}(\mathcal {H})$
for
$A_{n} \in \mathcal {B}(\mathcal {H})$
for
![]() $n \in \mathbb {N} \cup \{0\}$
, we define the Bohr operator
$n \in \mathbb {N} \cup \{0\}$
, we define the Bohr operator
![]() $M_{r}(f)$
as the scalar valued case. That is,
$M_{r}(f)$
as the scalar valued case. That is,
![]() $M_{r}(f)= \sum _{n=0}^{\infty } \left \lVert A_{n}\right \rVert |z|^n$
. It can be easily seen that the operator
$M_{r}(f)= \sum _{n=0}^{\infty } \left \lVert A_{n}\right \rVert |z|^n$
. It can be easily seen that the operator
![]() $M_{r}$
satisfies the same property as in Theorem 1.1. In fact, for
$M_{r}$
satisfies the same property as in Theorem 1.1. In fact, for
![]() $f,g :\mathbb {D} \rightarrow \mathcal {B}(\mathcal {H})$
with
$f,g :\mathbb {D} \rightarrow \mathcal {B}(\mathcal {H})$
with
![]() $f(z)= \sum _{n=0}^{\infty } A_{n} z^n$
and
$f(z)= \sum _{n=0}^{\infty } A_{n} z^n$
and
![]() $g(z)= \sum _{n=0}^{\infty } B_{n} z^n$
in
$g(z)= \sum _{n=0}^{\infty } B_{n} z^n$
in
![]() $\mathbb {D}$
with
$\mathbb {D}$
with
![]() $A_{n}, B_{n} \in \mathcal {B}(\mathcal {H})$
for
$A_{n}, B_{n} \in \mathcal {B}(\mathcal {H})$
for
![]() $n \in \mathbb {N} \cup \{0\}$
, we have
$n \in \mathbb {N} \cup \{0\}$
, we have
 $$ \begin{align} M_{r}(f+g) = \sum_{n=0}^{\infty} \left\lVert A_{n}+B_{n}\right\rVert r^n \leq \sum_{n=0}^{\infty} \left\lVert A_{n}\right\rVert r^n + \sum_{n=0}^{\infty} \left\lVert B_{n}\right\rVert r^n= M_{r}(f) + M_{r}(g). \end{align} $$
$$ \begin{align} M_{r}(f+g) = \sum_{n=0}^{\infty} \left\lVert A_{n}+B_{n}\right\rVert r^n \leq \sum_{n=0}^{\infty} \left\lVert A_{n}\right\rVert r^n + \sum_{n=0}^{\infty} \left\lVert B_{n}\right\rVert r^n= M_{r}(f) + M_{r}(g). \end{align} $$
Using (2.1), it is easy to see that if
![]() $F(z)= \sum _{k\in \mathbb {Z}} f_{k}(z)$
is analytic function in
$F(z)= \sum _{k\in \mathbb {Z}} f_{k}(z)$
is analytic function in
![]() $\mathbb {D}$
, then
$\mathbb {D}$
, then
![]() $M_{r}(F) \leq \sum _{k\in \mathbb {Z}} M_{r}(f_{k})$
, where
$M_{r}(F) \leq \sum _{k\in \mathbb {Z}} M_{r}(f_{k})$
, where
![]() $f_{k}: \mathbb {D} \rightarrow \mathcal {B}(\mathcal {H})$
is analytic function in
$f_{k}: \mathbb {D} \rightarrow \mathcal {B}(\mathcal {H})$
is analytic function in
![]() $\mathbb {D}$
for each
$\mathbb {D}$
for each
![]() $k \in \mathbb {Z}$
. On the other hand, we note that
$k \in \mathbb {Z}$
. On the other hand, we note that
![]() $M_{r}(\beta f)= |\beta |M_{r}(f)$
for any
$M_{r}(\beta f)= |\beta |M_{r}(f)$
for any
![]() $\beta \in \mathbb {C}$
and
$\beta \in \mathbb {C}$
and
![]() $M_{r}(z^pf)=r^p M_{r}(f)$
. We observe that
$M_{r}(z^pf)=r^p M_{r}(f)$
. We observe that
![]() $(fg)(z)=\sum _{n=0}^{\infty } A_{n} (z^n g(z))$
and hence
$(fg)(z)=\sum _{n=0}^{\infty } A_{n} (z^n g(z))$
and hence
 $$ \begin{align} M_{r}(fg) \leq \sum_{n=0}^{\infty} \left\lVert A_{n}\right\rVert r^n M_{r}(g)= M_{r}(f)M_{r}(g). \end{align} $$
$$ \begin{align} M_{r}(fg) \leq \sum_{n=0}^{\infty} \left\lVert A_{n}\right\rVert r^n M_{r}(g)= M_{r}(f)M_{r}(g). \end{align} $$
Clearly,
![]() $M_{r}(I)=1$
. The following result has been established in [Reference Abu Muhanna, Ali, Ng and Lee2].
$M_{r}(I)=1$
. The following result has been established in [Reference Abu Muhanna, Ali, Ng and Lee2].
Lemma 2.3 [Reference Abu Muhanna, Ali, Ng and Lee2]
Let
![]() $\phi :\mathbb {D} \rightarrow \mathbb {D}$
be analytic function with
$\phi :\mathbb {D} \rightarrow \mathbb {D}$
be analytic function with
![]() $\phi (0)=0$
. Then
$\phi (0)=0$
. Then
![]() $M_{r}(\phi ) \leq |z|$
for
$M_{r}(\phi ) \leq |z|$
for
![]() $|z|=r \leq 1/3$
.
$|z|=r \leq 1/3$
.
The following result is the operator-valued subordination result for Bohr operator, which has been first proved in [Reference Bhowmik and Das11]. By using Lemma 2.3, we give an alternative proof.
Theorem 2.1 Let
![]() $f,g:\mathbb {D} \rightarrow \mathcal {B}(\mathcal {H})$
be holomorphic functions such that
$f,g:\mathbb {D} \rightarrow \mathcal {B}(\mathcal {H})$
be holomorphic functions such that
![]() $f \prec g$
. Then
$f \prec g$
. Then
Proof Let
![]() $f(z)= \sum _{n=0}^{\infty } A_{n} z^n$
and
$f(z)= \sum _{n=0}^{\infty } A_{n} z^n$
and
![]() $g(z)= \sum _{n=0}^{\infty } B_{n} z^n$
in
$g(z)= \sum _{n=0}^{\infty } B_{n} z^n$
in
![]() $\mathbb {D}$
with
$\mathbb {D}$
with
![]() $A_{n}, B_{n} \in \mathcal {B}(\mathcal {H})$
for
$A_{n}, B_{n} \in \mathcal {B}(\mathcal {H})$
for
![]() $n \in \mathbb {N} \cup \{0\}$
. Since
$n \in \mathbb {N} \cup \{0\}$
. Since
![]() $f \prec g$
in
$f \prec g$
in
![]() $\mathbb {D}$
, then there exists an analytic function
$\mathbb {D}$
, then there exists an analytic function
![]() $\phi :\mathbb {D} \rightarrow \mathbb {D}$
such that
$\phi :\mathbb {D} \rightarrow \mathbb {D}$
such that
![]() $\phi (0)=0$
and
$\phi (0)=0$
and
![]() $f(z)=g(\phi (z))$
in
$f(z)=g(\phi (z))$
in
![]() $\mathbb {D}$
. In view of (2.1), (2.2), and Lemma 2.3, for
$\mathbb {D}$
. In view of (2.1), (2.2), and Lemma 2.3, for
![]() $0\leq |z|=r\leq 1/3$
, we obtain
$0\leq |z|=r\leq 1/3$
, we obtain
 $$ \begin{align*} M_{r}(f)=M_{r}(g(\phi))&=M_{r}\left(\sum_{n=0}^{\infty}B_{n}(\phi(z))^n\right) \\& \leq \sum_{n=0}^{\infty} \left\lVert B_{n}\right\rVert(M_{r}(\phi(z)))^n \leq \sum_{n=0}^{\infty} \left\lVert B_{n}\right\rVert r^n=M_{r}(g). \end{align*} $$
$$ \begin{align*} M_{r}(f)=M_{r}(g(\phi))&=M_{r}\left(\sum_{n=0}^{\infty}B_{n}(\phi(z))^n\right) \\& \leq \sum_{n=0}^{\infty} \left\lVert B_{n}\right\rVert(M_{r}(\phi(z)))^n \leq \sum_{n=0}^{\infty} \left\lVert B_{n}\right\rVert r^n=M_{r}(g). \end{align*} $$
This completes the proof.
In particular, for the scalar-valued functions
![]() $f,g:\mathbb {D} \rightarrow \mathbb {C}$
, Theorem 2.1 reduces to the result of Abu Muhanna et al. [Reference Abu Muhanna, Ali, Ng and Lee2], and Bhowmik and Das [Reference Bhowmik and Das10]. In view of Theorem 2.1, we obtain the following interesting result.
$f,g:\mathbb {D} \rightarrow \mathbb {C}$
, Theorem 2.1 reduces to the result of Abu Muhanna et al. [Reference Abu Muhanna, Ali, Ng and Lee2], and Bhowmik and Das [Reference Bhowmik and Das10]. In view of Theorem 2.1, we obtain the following interesting result.
Theorem 2.2 Let
![]() $f,g,h:\mathbb {D} \rightarrow \mathcal {B}(\mathcal {H})$
be holomorphic functions such that
$f,g,h:\mathbb {D} \rightarrow \mathcal {B}(\mathcal {H})$
be holomorphic functions such that
![]() $f(z)=h(z)g(\phi (z))$
for some analytic function
$f(z)=h(z)g(\phi (z))$
for some analytic function
![]() $\phi :\mathbb {D} \rightarrow \mathbb {D}$
with
$\phi :\mathbb {D} \rightarrow \mathbb {D}$
with
![]() $\phi (0)=0$
. If
$\phi (0)=0$
. If
![]() $\left \lVert h(z)\right \rVert \leq M$
for
$\left \lVert h(z)\right \rVert \leq M$
for
![]() $|z|<\beta \leq 1$
and
$|z|<\beta \leq 1$
and
![]() $h(0)=\alpha I$
with
$h(0)=\alpha I$
with
![]() $|\alpha | \leq M$
, then
$|\alpha | \leq M$
, then
![]() $M_{r}(f) \leq M \, M_{r}(g)$
for
$M_{r}(f) \leq M \, M_{r}(g)$
for
![]() $0 \leq r \leq \beta /3$
.
$0 \leq r \leq \beta /3$
.
Proof From (2.2), we have
The assumption
![]() $\left \lVert h(z)\right \rVert \leq M$
in the disk
$\left \lVert h(z)\right \rVert \leq M$
in the disk
![]() $\mathbb {D}_{\beta }:=\{z \in \mathbb {C}:|z|<\beta \}$
shows that
$\mathbb {D}_{\beta }:=\{z \in \mathbb {C}:|z|<\beta \}$
shows that
![]() $h_{1}:\mathbb {D} \rightarrow \mathcal {B}(\mathcal {H})$
defined by
$h_{1}:\mathbb {D} \rightarrow \mathcal {B}(\mathcal {H})$
defined by
![]() $h_{1}(z)=h(z)/M$
is holomorphic and
$h_{1}(z)=h(z)/M$
is holomorphic and
![]() $\left \lVert h_{1}(z)\right \rVert \leq 1$
in
$\left \lVert h_{1}(z)\right \rVert \leq 1$
in
![]() $\mathbb {D}_{\beta }$
such that
$\mathbb {D}_{\beta }$
such that
![]() $h_{1}(0)=(\alpha /M)I$
. Since
$h_{1}(0)=(\alpha /M)I$
. Since
![]() $|\alpha | \leq M$
, from (1.6), we obtain
$|\alpha | \leq M$
, from (1.6), we obtain
Furthermore, in view of Theorem 2.1, we have
By using (2.6) and (2.7) in (2.5), we obtain
This completes the proof.
Remark 2.1
-
(1) For a particular case
 $h(z)\equiv I$
, Theorem 2.2 reduces to Theorem 2.1. By taking
$h(z)\equiv I$
, Theorem 2.2 reduces to Theorem 2.1. By taking
 $f,g,h :\mathbb {D} \rightarrow \mathbb {C}$
are analytic functions in Theorem 2.2, we obtain the scalar-valued quasi-subordination result, which has been established in [Reference Alkhaleefah, Kayumov and Ponnusamy5].
$f,g,h :\mathbb {D} \rightarrow \mathbb {C}$
are analytic functions in Theorem 2.2, we obtain the scalar-valued quasi-subordination result, which has been established in [Reference Alkhaleefah, Kayumov and Ponnusamy5]. -
(2) When
 $\left \lVert h(z)\right \rVert \leq 1$
in
$\left \lVert h(z)\right \rVert \leq 1$
in
 $\mathbb {D}$
, we deduce that
$\mathbb {D}$
, we deduce that
 $M_{r}(f) \leq M_{r}(g)$
for
$M_{r}(f) \leq M_{r}(g)$
for
 $|z|=r \leq 1/3$
.
$|z|=r \leq 1/3$
.
We now prove the following interesting result, which is an analog of von Neumann inequality (1.2).
Theorem 2.3 Let
![]() $f:\mathbb {D} \rightarrow \mathcal {B}(\mathcal {H})$
be analytic in
$f:\mathbb {D} \rightarrow \mathcal {B}(\mathcal {H})$
be analytic in
![]() $\mathbb {D}$
and continuous in
$\mathbb {D}$
and continuous in
![]() $\overline {\mathbb {D}}$
such that
$\overline {\mathbb {D}}$
such that
![]() $f(0)=\alpha I$
for some
$f(0)=\alpha I$
for some
![]() $\alpha \in \mathbb {C}$
with
$\alpha \in \mathbb {C}$
with
![]() $|\alpha |<1$
. Then
$|\alpha |<1$
. Then
where
![]() $\phi : \mathbb {D} \rightarrow \mathbb {D}$
is analytic function with
$\phi : \mathbb {D} \rightarrow \mathbb {D}$
is analytic function with
![]() $\phi (0)=0$
.
$\phi (0)=0$
.
Proof Let
![]() $f(z)= \sum _{n=0}^{\infty } A_{n} z^n$
in
$f(z)= \sum _{n=0}^{\infty } A_{n} z^n$
in
![]() $\mathbb {D}$
, where
$\mathbb {D}$
, where
![]() $A_{0}=\alpha I$
and
$A_{0}=\alpha I$
and
![]() $A_{n} \in \mathcal {B}(\mathcal {H})$
for
$A_{n} \in \mathcal {B}(\mathcal {H})$
for
![]() $n \in \mathbb {N} \cup \{0\}$
. Then, for
$n \in \mathbb {N} \cup \{0\}$
. Then, for
![]() $r \leq 1/3$
, Theorem 2.1 gives
$r \leq 1/3$
, Theorem 2.1 gives
 $$ \begin{align} M_{r}(f(\phi)) \leq \sum_{n=0}^{\infty} \left\lVert A_{n}\right\rVert r^n= M_{r}(f). \end{align} $$
$$ \begin{align} M_{r}(f(\phi)) \leq \sum_{n=0}^{\infty} \left\lVert A_{n}\right\rVert r^n= M_{r}(f). \end{align} $$
In view of (1.6), for
![]() $0\leq r \leq 1/3$
, we obtain
$0\leq r \leq 1/3$
, we obtain
![]() $M_{r}(f) \leq \left \lVert f\right \rVert _{\infty }$
which together with (2.10) gives (2.9).
$M_{r}(f) \leq \left \lVert f\right \rVert _{\infty }$
which together with (2.10) gives (2.9).
3 Bohr theorem for operator-valued polyanalytic functions
Polyanalytic functions f of order p defined in a simply connected domain
![]() $\Omega \subseteq \mathbb {C}$
are complex-valued polynomials in the variable
$\Omega \subseteq \mathbb {C}$
are complex-valued polynomials in the variable
![]() $\overline {z}$
with analytic functions are their coefficients. That is, f has the following form
$\overline {z}$
with analytic functions are their coefficients. That is, f has the following form
![]() $ f(z)= \sum _{l=0}^{p-1} \overline {z}^p \, f_{l}(z), $
where
$ f(z)= \sum _{l=0}^{p-1} \overline {z}^p \, f_{l}(z), $
where
![]() $f_{l}$
’s are analytic functions in
$f_{l}$
’s are analytic functions in
![]() $\Omega $
. Equivalently, polyanalytic functions can also be defined as the
$\Omega $
. Equivalently, polyanalytic functions can also be defined as the
![]() $\mathcal {C}^p(\Omega )$
-solutions of the generalized Cauchy–Riemann equations
$\mathcal {C}^p(\Omega )$
-solutions of the generalized Cauchy–Riemann equations
![]() $\partial ^{p} f/ \partial \overline {z}^p=0$
in
$\partial ^{p} f/ \partial \overline {z}^p=0$
in
![]() $\Omega $
(the Cauchy–Riemann equations of order p). Throughout this paper, we assume that
$\Omega $
(the Cauchy–Riemann equations of order p). Throughout this paper, we assume that
![]() $p \geq 2$
.
$p \geq 2$
.
In
![]() $1908$
, Kolossov [Reference Kolossov20] first introduced polyanalytic functions in connection with his research in the mathematical theory of elasticity. Polyanalytic function theory has been extensively studied by Balk [Reference Balk, Gonchar, Havin and Nikolski9]. In
$1908$
, Kolossov [Reference Kolossov20] first introduced polyanalytic functions in connection with his research in the mathematical theory of elasticity. Polyanalytic function theory has been extensively studied by Balk [Reference Balk, Gonchar, Havin and Nikolski9]. In
![]() $2011$
, Agranovsky [Reference Agranovsky3] characterized the polyanalytic functions by meromorphic extensions into chains of circles. It is worth mentioning that the properties of polyanalytic functions can be different from those of analytic functions (see [Reference Balk, Gonchar, Havin and Nikolski9]). By considering the polyanalytic function
$2011$
, Agranovsky [Reference Agranovsky3] characterized the polyanalytic functions by meromorphic extensions into chains of circles. It is worth mentioning that the properties of polyanalytic functions can be different from those of analytic functions (see [Reference Balk, Gonchar, Havin and Nikolski9]). By considering the polyanalytic function
![]() $f(z)=1-z\overline {z}$
, one can easily see that f vanishes on the boundary of the unit disk
$f(z)=1-z\overline {z}$
, one can easily see that f vanishes on the boundary of the unit disk
![]() $\mathbb {D}$
without vanishing identically in
$\mathbb {D}$
without vanishing identically in
![]() $\mathbb {D}$
. Studying polyanalytic functions also reveals some new properties of analytic functions. The study of polyanalytic functions is closely related to numerous research topics of complex analysis, e.g., function theory of several complex variables, the theory of distribution of values of meromorphic functions, the theory of meromorphic curves, and the theory of boundary properties of analytic functions. In
$\mathbb {D}$
. Studying polyanalytic functions also reveals some new properties of analytic functions. The study of polyanalytic functions is closely related to numerous research topics of complex analysis, e.g., function theory of several complex variables, the theory of distribution of values of meromorphic functions, the theory of meromorphic curves, and the theory of boundary properties of analytic functions. In
![]() $2019$
, Hachadi and Youssfi [Reference Hachadi and Youssfi18] have studied several properties of polyanalytic reproducing kernels. In
$2019$
, Hachadi and Youssfi [Reference Hachadi and Youssfi18] have studied several properties of polyanalytic reproducing kernels. In
![]() $2021$
, Abdulhadi and Hajj [Reference Abdulhadi and Hajj1] extensively studied univalency criteria, Landau’s theorem, arc-length problem, and the Bohr phenomenon problem for polyanalytic functions in
$2021$
, Abdulhadi and Hajj [Reference Abdulhadi and Hajj1] extensively studied univalency criteria, Landau’s theorem, arc-length problem, and the Bohr phenomenon problem for polyanalytic functions in
![]() $\mathbb {D}$
.
$\mathbb {D}$
.
Since complex-valued polyanalytic functions are polynomials in
![]() $\overline {z}$
in simply connected domain
$\overline {z}$
in simply connected domain
![]() $\Omega $
, this leads to study the operator-valued polyanalytic functions. A operator-valued polyanalytic function F of order p in
$\Omega $
, this leads to study the operator-valued polyanalytic functions. A operator-valued polyanalytic function F of order p in
![]() $\Omega $
is a polynomial in
$\Omega $
is a polynomial in
![]() $\overline {z}$
with operator-valued analytic functions as its coefficients. That is, F has the following form:
$\overline {z}$
with operator-valued analytic functions as its coefficients. That is, F has the following form:
 $$ \begin{align*} F(z)= \sum_{l=0}^{p-1} \overline{z}^p \, f_{l}(z), \end{align*} $$
$$ \begin{align*} F(z)= \sum_{l=0}^{p-1} \overline{z}^p \, f_{l}(z), \end{align*} $$
where
![]() $f_{l}: \Omega \rightarrow \mathcal {B}(\mathcal {H})$
are analytic functions for
$f_{l}: \Omega \rightarrow \mathcal {B}(\mathcal {H})$
are analytic functions for
![]() $l=0,1, \ldots , p-1$
and
$l=0,1, \ldots , p-1$
and
![]() $f_{p-1} \not \equiv 0$
. Now, we consider the simply connected domain
$f_{p-1} \not \equiv 0$
. Now, we consider the simply connected domain
![]() $\Omega $
containing
$\Omega $
containing
![]() $\mathbb {D}$
.
$\mathbb {D}$
.
Although Bohr radius and Bohr phenomenon have been extensively studied, no attempt has been made so far to obtain operator-valued analogs of Bohr phenomenon for polyanalytic functions. Therefore, our main aim of this section is to obtain the Bohr inequality under appropriate considerations and necessary conditions. In the following result, we establish operator-valued analogs of Bohr inequality in simply connected domain
![]() $\Omega $
containing
$\Omega $
containing
![]() $\mathbb {D}$
.
$\mathbb {D}$
.
Theorem 3.1 Let F be a polyanalytic function of order p in
![]() $\Omega $
with
$\Omega $
with
![]() $F(z)= \sum _{l=0}^{p-1} \overline {z}^l \, f_{l}(z) $
, where each
$F(z)= \sum _{l=0}^{p-1} \overline {z}^l \, f_{l}(z) $
, where each
![]() $f_{l}: \Omega \rightarrow \mathcal {B}(\mathcal {H})$
is an analytic function such that
$f_{l}: \Omega \rightarrow \mathcal {B}(\mathcal {H})$
is an analytic function such that
![]() $f_{l}(z)= \sum _{n=0}^{\infty } A_{n,l} z^n$
in
$f_{l}(z)= \sum _{n=0}^{\infty } A_{n,l} z^n$
in
![]() $\mathbb {D}$
and
$\mathbb {D}$
and
![]() $A_{n,l} \in \mathcal {B}(\mathcal {H})$
for
$A_{n,l} \in \mathcal {B}(\mathcal {H})$
for
![]() $n \in \mathbb {N} \cup \{0\}$
. Also, assume that:
$n \in \mathbb {N} \cup \{0\}$
. Also, assume that:
-
(a)
 $\left \lVert f_{0}(z)\right \rVert \leq 1$
in
$\left \lVert f_{0}(z)\right \rVert \leq 1$
in
 $\Omega $
such that
$\Omega $
such that
 $f_{0}(0)=\mathbf {0}$
and
$f_{0}(0)=\mathbf {0}$
and
 $f^{\prime }_{l}(0)=\alpha _{l} f^{\prime }_{0}(0)$
with
$f^{\prime }_{l}(0)=\alpha _{l} f^{\prime }_{0}(0)$
with
 $|\alpha _{l}| <k$
for
$|\alpha _{l}| <k$
for
 $k \in [0,1]$
and each
$k \in [0,1]$
and each
 $l=1,\ldots , p-1$
.
$l=1,\ldots , p-1$
. -
(b)
 $\omega _{l} : \Omega \rightarrow \mathcal {B}(\mathcal {H})$
is analytic with
$\omega _{l} : \Omega \rightarrow \mathcal {B}(\mathcal {H})$
is analytic with
 $\left \lVert \omega _{l}(z)\right \rVert \leq k$
in
$\left \lVert \omega _{l}(z)\right \rVert \leq k$
in
 $\Omega $
for
$\Omega $
for
 $k \in [0,1]$
, where
$k \in [0,1]$
, where
 $\omega _{l}(z)= f^{\prime }_{l}(z) (f^{\prime }_{0}(z))^{-1}$
in
$\omega _{l}(z)= f^{\prime }_{l}(z) (f^{\prime }_{0}(z))^{-1}$
in
 $\Omega $
such that
$\Omega $
such that
 $\omega _{l}(z)=\sum _{n=0}^{\infty } \omega _{n,l} z^n $
in
$\omega _{l}(z)=\sum _{n=0}^{\infty } \omega _{n,l} z^n $
in
 $\mathbb {D}$
, provided
$\mathbb {D}$
, provided
 $(f^{\prime }_{0}(z))^{-1}$
exists for all
$(f^{\prime }_{0}(z))^{-1}$
exists for all
 $z \in \Omega $
.
$z \in \Omega $
.
Then
![]() $M_{r}(F) \leq 1$
for
$M_{r}(F) \leq 1$
for
![]() $|z|=r \leq R_{f}= \min \{r_{f}(p), 1/(1+2\lambda _{\mathcal {H}})\}$
, where
$|z|=r \leq R_{f}= \min \{r_{f}(p), 1/(1+2\lambda _{\mathcal {H}})\}$
, where
![]() $r_{f}(p)$
is the smallest root in
$r_{f}(p)$
is the smallest root in
![]() $(0,1)$
of
$(0,1)$
of
Here,
![]() $\lambda _{\mathcal {H}}$
is given by (1.3).
$\lambda _{\mathcal {H}}$
is given by (1.3).
Proof Let
![]() $F(z)= \sum _{l=0}^{p-1} \overline {z}^l \, f_{l}(z) $
with
$F(z)= \sum _{l=0}^{p-1} \overline {z}^l \, f_{l}(z) $
with
![]() $f_{l}(z)= \sum _{n=0}^{\infty } A_{n,l} \,z^n$
in
$f_{l}(z)= \sum _{n=0}^{\infty } A_{n,l} \,z^n$
in
![]() $\mathbb {D}$
. Then
$\mathbb {D}$
. Then
 $$ \begin{align} M_{r}(F)= M_{r} \left(\sum_{l=0}^{p-1} \overline{z}^l \, f_{l}(z)\right) \leq \sum_{l=0}^{p-1} r^l M_{r}(f_{l}) \,\,\,\,\, \mbox{for} \,\,\,\, |z|=r<1. \end{align} $$
$$ \begin{align} M_{r}(F)= M_{r} \left(\sum_{l=0}^{p-1} \overline{z}^l \, f_{l}(z)\right) \leq \sum_{l=0}^{p-1} r^l M_{r}(f_{l}) \,\,\,\,\, \mbox{for} \,\,\,\, |z|=r<1. \end{align} $$
Since
![]() $\omega _{l}(z)=f^{\prime }_{l}(z) (f^{\prime }_{0}(z))^{-1}$
in
$\omega _{l}(z)=f^{\prime }_{l}(z) (f^{\prime }_{0}(z))^{-1}$
in
![]() $\Omega $
with
$\Omega $
with
![]() $\left \lVert \omega _{l}(z)\right \rVert \leq k$
in
$\left \lVert \omega _{l}(z)\right \rVert \leq k$
in
![]() $\Omega $
for each l such that
$\Omega $
for each l such that
![]() $f^{\prime }_{l}(0)=\alpha _{l} f^{\prime }_{0}(0)$
, it follows that
$f^{\prime }_{l}(0)=\alpha _{l} f^{\prime }_{0}(0)$
, it follows that
![]() $f^{\prime }_{l}(z)= \omega _{l}(z) f^{\prime }_{0}(z)$
in
$f^{\prime }_{l}(z)= \omega _{l}(z) f^{\prime }_{0}(z)$
in
![]() $\Omega $
with
$\Omega $
with
![]() $\omega _{l}(0)=\alpha _{l}I$
, where
$\omega _{l}(0)=\alpha _{l}I$
, where
![]() $|\alpha _{l}|<k$
for each
$|\alpha _{l}|<k$
for each
![]() $l=1, \ldots , p-1$
. Let
$l=1, \ldots , p-1$
. Let
![]() $\lambda _{\mathcal {H}}$
be given by (1.3). In view of Theorem 1.2, for
$\lambda _{\mathcal {H}}$
be given by (1.3). In view of Theorem 1.2, for
![]() $|z|=r \leq 1/(1+2\lambda _{\mathcal {H}})$
, we have
$|z|=r \leq 1/(1+2\lambda _{\mathcal {H}})$
, we have
![]() $M_{r}(\omega _{l}) \leq k$
, which together with (2.2) gives
$M_{r}(\omega _{l}) \leq k$
, which together with (2.2) gives
 $$ \begin{align} M_{r}(f_{l})= \int \limits_{0}^{r} M_{r}(f^{\prime}_{l})dt= \int\limits_{0}^{r} M_{r}(\omega_{l}f^{\prime}_{0})dt \leq k\,\int\limits_{0}^{r} M_{r}(f^{\prime}_{0})dt =k\, M_{r}(f_{0}). \end{align} $$
$$ \begin{align} M_{r}(f_{l})= \int \limits_{0}^{r} M_{r}(f^{\prime}_{l})dt= \int\limits_{0}^{r} M_{r}(\omega_{l}f^{\prime}_{0})dt \leq k\,\int\limits_{0}^{r} M_{r}(f^{\prime}_{0})dt =k\, M_{r}(f_{0}). \end{align} $$
Using (3.2) and (3.3), for
![]() $|z|=r \leq 1/(1+2\lambda _{\mathcal {H}})$
, we obtain
$|z|=r \leq 1/(1+2\lambda _{\mathcal {H}})$
, we obtain
 $$ \begin{align} M_{r}(F) \leq k\sum_{l=0}^{p-1} r^l M_{r}(f_{0}) = k M_{r}(f_{0}) \left(\frac{1-r^p}{1-r}\right). \end{align} $$
$$ \begin{align} M_{r}(F) \leq k\sum_{l=0}^{p-1} r^l M_{r}(f_{0}) = k M_{r}(f_{0}) \left(\frac{1-r^p}{1-r}\right). \end{align} $$
We now wish to find the upper bound for
![]() $M_{r}(f_{0})$
. We observe that
$M_{r}(f_{0})$
. We observe that
![]() $f_{0}: \Omega \rightarrow \mathcal {B}(\mathcal {H})$
is analytic function with
$f_{0}: \Omega \rightarrow \mathcal {B}(\mathcal {H})$
is analytic function with
![]() $\left \lVert f_{0}(z)\right \rVert \leq 1$
in
$\left \lVert f_{0}(z)\right \rVert \leq 1$
in
![]() $\Omega $
such that
$\Omega $
such that
![]() $f_{0}(z)= \sum _{n=0}^{\infty } A_{n,0} z^n$
in
$f_{0}(z)= \sum _{n=0}^{\infty } A_{n,0} z^n$
in
![]() $\mathbb {D}$
, where
$\mathbb {D}$
, where
![]() $f_{0}(0)=A_{0,0}=\mathbf {0}$
. Then, in view of (1.3), we have
$f_{0}(0)=A_{0,0}=\mathbf {0}$
. Then, in view of (1.3), we have
![]() $\left \lVert A_{n,0}\right \rVert \leq \lambda _{\mathcal {H}}$
for
$\left \lVert A_{n,0}\right \rVert \leq \lambda _{\mathcal {H}}$
for
![]() $n \geq 1$
, and hence
$n \geq 1$
, and hence
 $$ \begin{align} M_{r}(f_{0}) = \sum_{n=0}^{\infty} \left\lVert A_{n,0}\right\rVert\, r^n \leq \lambda_{\mathcal{H}} \left(\frac{r}{1-r}\right). \end{align} $$
$$ \begin{align} M_{r}(f_{0}) = \sum_{n=0}^{\infty} \left\lVert A_{n,0}\right\rVert\, r^n \leq \lambda_{\mathcal{H}} \left(\frac{r}{1-r}\right). \end{align} $$
In view of (3.4) and (3.5), for
![]() $r \leq 1/(1+2\lambda _{\mathcal {H}})$
, we obtain
$r \leq 1/(1+2\lambda _{\mathcal {H}})$
, we obtain
 $$ \begin{align} M_{r}(F) \leq k \, \lambda_{\mathcal{H}}\left( \frac{r}{1-r}\right) \left(\frac{1-r^p}{1-r}\right). \end{align} $$
$$ \begin{align} M_{r}(F) \leq k \, \lambda_{\mathcal{H}}\left( \frac{r}{1-r}\right) \left(\frac{1-r^p}{1-r}\right). \end{align} $$
Therefore,
![]() $M_{r}(F) \leq 1$
for
$M_{r}(F) \leq 1$
for
![]() $r \leq \min \{1/(1+2\lambda _{\mathcal {H}}), r_{f}(p)\}$
, where
$r \leq \min \{1/(1+2\lambda _{\mathcal {H}}), r_{f}(p)\}$
, where
![]() $r_{f}(p)$
is the smallest root in
$r_{f}(p)$
is the smallest root in
![]() $(0,1)$
of
$(0,1)$
of
 $$\begin{align*}k\, \lambda_{\mathcal{H}}\left( \frac{r}{1-r}\right) \left(\frac{1-r^p}{1-r}\right) = 1, \end{align*}$$
$$\begin{align*}k\, \lambda_{\mathcal{H}}\left( \frac{r}{1-r}\right) \left(\frac{1-r^p}{1-r}\right) = 1, \end{align*}$$
which is equivalent to
![]() $(1-r)^2 -k\, \lambda _{\mathcal {H}}\,r + k\,\lambda _{\mathcal {H}}\, r^{p+1}=0$
. This completes the proof.
$(1-r)^2 -k\, \lambda _{\mathcal {H}}\,r + k\,\lambda _{\mathcal {H}}\, r^{p+1}=0$
. This completes the proof.
As a consequence of Theorem 3.1, we obtain Bohr-type inequality for bi-analytic functions in a domain
![]() $\Omega $
.
$\Omega $
.
Corollary 3.7 Let F be a bi-analytic function in a domain
![]() $\Omega $
with the series expansion as in Theorem 3.1. Also, assume all the hypotheses as in Theorem 3.1. Then
$\Omega $
with the series expansion as in Theorem 3.1. Also, assume all the hypotheses as in Theorem 3.1. Then
![]() $M_{r}(F)\leq 1$
for
$M_{r}(F)\leq 1$
for
![]() $|z|=r \leq \min \{r_{f}(2), 1/(1+2\lambda _{\mathcal {H}})\}$
, where
$|z|=r \leq \min \{r_{f}(2), 1/(1+2\lambda _{\mathcal {H}})\}$
, where
![]() $r_{f}(2)$
is the smallest root in
$r_{f}(2)$
is the smallest root in
![]() $(0,1)$
of
$(0,1)$
of
where
![]() $\lambda _{\mathcal {H}}$
is given by (1.3).
$\lambda _{\mathcal {H}}$
is given by (1.3).
For
![]() $\Omega =\Omega _{\gamma }$
, we have
$\Omega =\Omega _{\gamma }$
, we have
![]() $\lambda _{\mathcal {H}}=\lambda _{\mathcal {H}}(\Omega _{\gamma })\leq 1/(1+\gamma )$
(see [Reference Allu and Halder6]). In view of Theorem 3.1, we obtain the following corollaries.
$\lambda _{\mathcal {H}}=\lambda _{\mathcal {H}}(\Omega _{\gamma })\leq 1/(1+\gamma )$
(see [Reference Allu and Halder6]). In view of Theorem 3.1, we obtain the following corollaries.
Corollary 3.9 Let F be a polyanalytic function in
![]() $\Omega _{\gamma }$
with the series expansion as in Theorem 3.1. Also, assume all the hypotheses as in Theorem 3.1. Then
$\Omega _{\gamma }$
with the series expansion as in Theorem 3.1. Also, assume all the hypotheses as in Theorem 3.1. Then
![]() $M_{r}(F)\leq 1$
for
$M_{r}(F)\leq 1$
for
![]() $|z|=r \leq \min \{r_{f}(p,\gamma ), (1+\gamma )/(3+\gamma )\}$
, where
$|z|=r \leq \min \{r_{f}(p,\gamma ), (1+\gamma )/(3+\gamma )\}$
, where
![]() $r_{f}(p,\gamma )$
is the smallest root in
$r_{f}(p,\gamma )$
is the smallest root in
![]() $(0,1)$
of
$(0,1)$
of
The following result is the limiting case of Corollary 3.9. Consider the domain
![]() $\tilde {\Omega }=\{z: {\operatorname {Re}\,} z<1\}$
, which can be obtained as the limiting case of the domain
$\tilde {\Omega }=\{z: {\operatorname {Re}\,} z<1\}$
, which can be obtained as the limiting case of the domain
![]() $\Omega _{\gamma }$
by considering
$\Omega _{\gamma }$
by considering
![]() $\gamma \rightarrow 1^{-}$
.
$\gamma \rightarrow 1^{-}$
.
Corollary 3.11 Let F be a polyanalytic function in
![]() $\tilde {\Omega }$
with the series expansion as in Theorem 3.1. Also, assume all the hypotheses as in Theorem 3.1. Then
$\tilde {\Omega }$
with the series expansion as in Theorem 3.1. Also, assume all the hypotheses as in Theorem 3.1. Then
![]() $M_{r}(F)\leq 1$
for
$M_{r}(F)\leq 1$
for
![]() $|z|=r \leq \min \{r_{f}(p,1), 1/2\}$
, where
$|z|=r \leq \min \{r_{f}(p,1), 1/2\}$
, where
![]() $r_{f}(p,1)$
is the smallest root in
$r_{f}(p,1)$
is the smallest root in
![]() $(0,1)$
of
$(0,1)$
of
In the next result, we obtain Bohr radius for the polyanalytic function
![]() $F(z)= \sum _{l=0}^{p-1} \overline {z}^l \, f_{l}(z) $
, where
$F(z)= \sum _{l=0}^{p-1} \overline {z}^l \, f_{l}(z) $
, where
![]() $f_{0}$
is a subordinate to a convex biholomorphic function in the unit disk
$f_{0}$
is a subordinate to a convex biholomorphic function in the unit disk
![]() $\mathbb {D}$
.
$\mathbb {D}$
.
Theorem 3.2 Let F be a polyanalytic function of order p in
![]() $\mathbb {D}$
with
$\mathbb {D}$
with
![]() $F(z)= \sum _{l=0}^{p-1} \overline {z}^l \, f_{l}(z) $
, where each
$F(z)= \sum _{l=0}^{p-1} \overline {z}^l \, f_{l}(z) $
, where each
![]() $f_{l}: \mathbb {D} \rightarrow \mathcal {B}(\mathcal {H})$
is an analytic function such that
$f_{l}: \mathbb {D} \rightarrow \mathcal {B}(\mathcal {H})$
is an analytic function such that
![]() $f_{l}(z)= \sum _{n=0}^{\infty } A_{n,l} z^n$
in
$f_{l}(z)= \sum _{n=0}^{\infty } A_{n,l} z^n$
in
![]() $\mathbb {D}$
and
$\mathbb {D}$
and
![]() $A_{n,l} \in \mathcal {B}(\mathcal {H})$
for
$A_{n,l} \in \mathcal {B}(\mathcal {H})$
for
![]() $n \in \mathbb {N} \cup \{0\}$
. Also, assume that:
$n \in \mathbb {N} \cup \{0\}$
. Also, assume that:
-
(1)
 $f_{0} \in S(g)$
such that
$f_{0} \in S(g)$
such that
 $f_{0}(0)=\mathbf {0}$
and
$f_{0}(0)=\mathbf {0}$
and
 $f^{\prime }_{l}(0)=\alpha _{l} f^{\prime }_{0}(0)$
with
$f^{\prime }_{l}(0)=\alpha _{l} f^{\prime }_{0}(0)$
with
 $|\alpha _{l}| <k$
for
$|\alpha _{l}| <k$
for
 $k \in [0,1]$
and each
$k \in [0,1]$
and each
 $l=1,\ldots , p-1$
, where
$l=1,\ldots , p-1$
, where
 $g:\mathbb {D} \rightarrow \mathcal {B}(\mathcal {H})$
is a convex biholomorphic function with
$g:\mathbb {D} \rightarrow \mathcal {B}(\mathcal {H})$
is a convex biholomorphic function with
 $g(z)= \sum _{n=0}^{\infty } g_{n} z^n$
in
$g(z)= \sum _{n=0}^{\infty } g_{n} z^n$
in
 $\mathbb {D}$
and
$\mathbb {D}$
and
 $g_{n} \in \mathcal {B}(\mathcal {H})$
for
$g_{n} \in \mathcal {B}(\mathcal {H})$
for
 $n \in \mathbb {N} \cup \{0\}$
.
$n \in \mathbb {N} \cup \{0\}$
. -
(2)
 $\omega _{l} : \mathbb {D} \rightarrow \mathcal {B}(\mathcal {H})$
is an analytic function with
$\omega _{l} : \mathbb {D} \rightarrow \mathcal {B}(\mathcal {H})$
is an analytic function with
 $\left \lVert \omega _{l}(z)\right \rVert \leq k$
in
$\left \lVert \omega _{l}(z)\right \rVert \leq k$
in
 $\mathbb {D}$
for
$\mathbb {D}$
for
 $k \in [0,1]$
, where
$k \in [0,1]$
, where
 $\omega _{l}(z)= f^{\prime }_{l}(z) (f^{\prime }_{0}(z))^{-1}$
in
$\omega _{l}(z)= f^{\prime }_{l}(z) (f^{\prime }_{0}(z))^{-1}$
in
 $\mathbb {D}$
such that
$\mathbb {D}$
such that
 $\omega _{l}(z)=\sum _{n=0}^{\infty } \omega _{n,l} z^n $
in
$\omega _{l}(z)=\sum _{n=0}^{\infty } \omega _{n,l} z^n $
in
 $\mathbb {D}$
, provided
$\mathbb {D}$
, provided
 $(f^{\prime }_{0}(z))^{-1}$
exists for all
$(f^{\prime }_{0}(z))^{-1}$
exists for all
 $z \in \mathbb {D}$
.
$z \in \mathbb {D}$
.
Then
![]() $M_{r}(F) \leq 1$
for
$M_{r}(F) \leq 1$
for
![]() $|z|=r \leq R_{C}= \min \{r_{C}(p,k,\beta ), 1/3\}$
, where
$|z|=r \leq R_{C}= \min \{r_{C}(p,k,\beta ), 1/3\}$
, where
![]() $r_{C}(p,k,\beta )$
is the smallest root in
$r_{C}(p,k,\beta )$
is the smallest root in
![]() $(0,1)$
of
$(0,1)$
of
where
![]() $\left \lVert g'(0)\right \rVert =\beta $
.
$\left \lVert g'(0)\right \rVert =\beta $
.
Proof From (3.4), it is enough to estimate the upper bound of
![]() $M_{r}(f_{0})$
. Let
$M_{r}(f_{0})$
. Let
![]() $g: \mathbb {D} \rightarrow \mathcal {B}(\mathcal {H})$
be univalent and convex biholomorphic function in
$g: \mathbb {D} \rightarrow \mathcal {B}(\mathcal {H})$
be univalent and convex biholomorphic function in
![]() $\mathbb {D}$
such that
$\mathbb {D}$
such that
![]() $g(z)=\sum _{n=0}^{\infty } g_{n}z^n$
, where
$g(z)=\sum _{n=0}^{\infty } g_{n}z^n$
, where
![]() $g_{n} \in \mathcal {B}(\mathcal {H})$
. Set
$g_{n} \in \mathcal {B}(\mathcal {H})$
. Set
![]() $\xi = e^{2\pi i/n}$
. Since g is convex, then by the similar argument used in proving [Reference Rogosinski26, Theorem X], we obtain
$\xi = e^{2\pi i/n}$
. Since g is convex, then by the similar argument used in proving [Reference Rogosinski26, Theorem X], we obtain
and hence
![]() $\Psi (z)=A_{n,0}z + A_{2n,0}z^{2}+ \cdots \prec g(z)$
for
$\Psi (z)=A_{n,0}z + A_{2n,0}z^{2}+ \cdots \prec g(z)$
for
![]() $z \in \mathbb {D}$
. Hence, there exits a holomorphic function
$z \in \mathbb {D}$
. Hence, there exits a holomorphic function
![]() $\omega : \mathbb {D} \rightarrow \mathbb {D}$
with
$\omega : \mathbb {D} \rightarrow \mathbb {D}$
with
![]() $\omega (0)=0$
such that
$\omega (0)=0$
such that
![]() $\Psi (z)=g(\omega (z))$
, which implies that
$\Psi (z)=g(\omega (z))$
, which implies that
![]() $\Psi '(0)=\omega '(0)g'(0)$
. That is,
$\Psi '(0)=\omega '(0)g'(0)$
. That is,
![]() $A_{n,0}=\omega '(0)g'(0)$
, which leads to
$A_{n,0}=\omega '(0)g'(0)$
, which leads to
Since
![]() $f_{l}(z)= \sum _{n=0}^{\infty } A_{n,l} z^n$
in
$f_{l}(z)= \sum _{n=0}^{\infty } A_{n,l} z^n$
in
![]() $\mathbb {D}$
, using (3.14) and the fact
$\mathbb {D}$
, using (3.14) and the fact
![]() $f_{0}(0)=\mathbf {0}$
, we obtain
$f_{0}(0)=\mathbf {0}$
, we obtain
 $$ \begin{align} M_{r}(f_{0})=\sum_{n=0}^{\infty}\left\lVert A_{n,0}\right\rVert r^n \leq \left(\frac{r}{1-r}\right) \, \left\lVert g'(0)\right\rVert=\beta \left(\frac{r}{1-r}\right). \end{align} $$
$$ \begin{align} M_{r}(f_{0})=\sum_{n=0}^{\infty}\left\lVert A_{n,0}\right\rVert r^n \leq \left(\frac{r}{1-r}\right) \, \left\lVert g'(0)\right\rVert=\beta \left(\frac{r}{1-r}\right). \end{align} $$
Since
![]() $F(z)= \sum _{l=0}^{p-1} \overline {z}^l \, f_{l}(z) $
with
$F(z)= \sum _{l=0}^{p-1} \overline {z}^l \, f_{l}(z) $
with
![]() $f_{l}(z)= \sum _{n=0}^{\infty } A_{n,l} \,z^n$
in
$f_{l}(z)= \sum _{n=0}^{\infty } A_{n,l} \,z^n$
in
![]() $\mathbb {D}$
, we have
$\mathbb {D}$
, we have
 $$ \begin{align} M_{r}(F)= M_{r} \left(\sum_{l=0}^{p-1} \overline{z}^l \, f_{l}(z)\right) \leq \sum_{l=0}^{p-1} r^l M_{r}(f_{l}) \,\,\,\,\, \mbox{for} \,\,\,\, |z|=r<1. \end{align} $$
$$ \begin{align} M_{r}(F)= M_{r} \left(\sum_{l=0}^{p-1} \overline{z}^l \, f_{l}(z)\right) \leq \sum_{l=0}^{p-1} r^l M_{r}(f_{l}) \,\,\,\,\, \mbox{for} \,\,\,\, |z|=r<1. \end{align} $$
By the given assumption
![]() $\omega _{l}(z)=f^{\prime }_{l}(z) (f^{\prime }_{0}(z))^{-1}$
in
$\omega _{l}(z)=f^{\prime }_{l}(z) (f^{\prime }_{0}(z))^{-1}$
in
![]() $\Omega $
with
$\Omega $
with
![]() $\left \lVert \omega _{l}(z)\right \rVert \leq k$
in
$\left \lVert \omega _{l}(z)\right \rVert \leq k$
in
![]() $\Omega $
for each l such that
$\Omega $
for each l such that
![]() $f^{\prime }_{l}(0)=\alpha _{l} f^{\prime }_{0}(0)$
, it follows that
$f^{\prime }_{l}(0)=\alpha _{l} f^{\prime }_{0}(0)$
, it follows that
![]() $f^{\prime }_{l}(z)= \omega _{l}(z) f^{\prime }_{0}(z)$
in
$f^{\prime }_{l}(z)= \omega _{l}(z) f^{\prime }_{0}(z)$
in
![]() $\Omega $
with
$\Omega $
with
![]() $\omega _{l}(0)=\alpha _{l}I$
, where
$\omega _{l}(0)=\alpha _{l}I$
, where
![]() $|\alpha _{l}|<k$
for each
$|\alpha _{l}|<k$
for each
![]() $l=1, \ldots , p-1$
. Let
$l=1, \ldots , p-1$
. Let
![]() $\lambda _{\mathcal {H}}$
be given by (1.3). For
$\lambda _{\mathcal {H}}$
be given by (1.3). For
![]() $\Omega _{\gamma }=\mathbb {D}$
, i.e.,
$\Omega _{\gamma }=\mathbb {D}$
, i.e.,
![]() $\gamma =0$
, we have
$\gamma =0$
, we have
![]() $\lambda _{\mathcal {H}} \leq 1$
(see [Reference Allu and Halder6]). In view of Theorem 1.2, for
$\lambda _{\mathcal {H}} \leq 1$
(see [Reference Allu and Halder6]). In view of Theorem 1.2, for
![]() $|z|=r \leq 1/3$
, we have
$|z|=r \leq 1/3$
, we have
![]() $M_{r}(\omega _{l}) \leq k$
, which together with (2.2) gives
$M_{r}(\omega _{l}) \leq k$
, which together with (2.2) gives
 $$ \begin{align} M_{r}(f_{l})= \int \limits_{0}^{r} M_{r}(f^{\prime}_{l})dt= \int\limits_{0}^{r} M_{r}(\omega_{l}f^{\prime}_{0})dt \leq k\,\int\limits_{0}^{r} M_{r}(f^{\prime}_{0})dt =k\, M_{r}(f_{0}). \end{align} $$
$$ \begin{align} M_{r}(f_{l})= \int \limits_{0}^{r} M_{r}(f^{\prime}_{l})dt= \int\limits_{0}^{r} M_{r}(\omega_{l}f^{\prime}_{0})dt \leq k\,\int\limits_{0}^{r} M_{r}(f^{\prime}_{0})dt =k\, M_{r}(f_{0}). \end{align} $$
Using (3.15)–(3.17), for
![]() $|z|=r \leq 1/3$
, we obtain
$|z|=r \leq 1/3$
, we obtain
 $$ \begin{align} M_{r}(F) \leq k\sum_{l=0}^{p-1} r^l M_{r}(f_{0}) = k M_{r}(f_{0}) \left(\frac{1-r^p}{1-r}\right) \leq k \beta \left(\frac{r}{1-r}\right) \left(\frac{1-r^p}{1-r}\right). \end{align} $$
$$ \begin{align} M_{r}(F) \leq k\sum_{l=0}^{p-1} r^l M_{r}(f_{0}) = k M_{r}(f_{0}) \left(\frac{1-r^p}{1-r}\right) \leq k \beta \left(\frac{r}{1-r}\right) \left(\frac{1-r^p}{1-r}\right). \end{align} $$
Hence,
![]() $M_{r}(F) \leq 1$
for
$M_{r}(F) \leq 1$
for
![]() $r \leq R_{C}= \min \{r_{C}(p,k,\beta ), 1/3\}$
, where
$r \leq R_{C}= \min \{r_{C}(p,k,\beta ), 1/3\}$
, where
![]() $r_{C}(p,k,\beta )$
is the smallest root in
$r_{C}(p,k,\beta )$
is the smallest root in
![]() $(0,1)$
of (3.13). This completes the proof.
$(0,1)$
of (3.13). This completes the proof.
Let
![]() $h:\mathbb {D} \rightarrow \mathcal {B}(\mathcal {H})$
be holomorphic and
$h:\mathbb {D} \rightarrow \mathcal {B}(\mathcal {H})$
be holomorphic and
![]() $g \in S(h)$
with the expansions
$g \in S(h)$
with the expansions
![]() $h(z)=\sum _{n=0}^{\infty } h_{n}z^n$
and
$h(z)=\sum _{n=0}^{\infty } h_{n}z^n$
and
![]() $g(z)=\sum _{n=0}^{\infty } g_{n}z^n$
, respectively, in
$g(z)=\sum _{n=0}^{\infty } g_{n}z^n$
, respectively, in
![]() $\mathbb {D}$
, where
$\mathbb {D}$
, where
![]() $h_{n},g_{n} \in \mathcal {B}(\mathcal {H})$
for
$h_{n},g_{n} \in \mathcal {B}(\mathcal {H})$
for
![]() $n \in \mathbb {N} \cup \{0\}$
. Then, in view of [Reference Bhowmik and Das11, Lemma 2], for
$n \in \mathbb {N} \cup \{0\}$
. Then, in view of [Reference Bhowmik and Das11, Lemma 2], for
![]() $|z|=r\leq 1/3$
, it is known that
$|z|=r\leq 1/3$
, it is known that
 $$ \begin{align} \sum_{n=1}^{\infty} \left\lVert g_{n}\right\rVert r^n \leq \sum_{n=1}^{\infty} \left\lVert h_{n}\right\rVert r^n. \end{align} $$
$$ \begin{align} \sum_{n=1}^{\infty} \left\lVert g_{n}\right\rVert r^n \leq \sum_{n=1}^{\infty} \left\lVert h_{n}\right\rVert r^n. \end{align} $$
In the following result, we obtain Bohr radius for the polyanalytic function
![]() $F(z)= \sum _{l=0}^{p-1} \overline {z}^l \, f_{l}(z) $
, where
$F(z)= \sum _{l=0}^{p-1} \overline {z}^l \, f_{l}(z) $
, where
![]() $f_{0}$
is subordinate to a starlike biholomorphic function in the unit disk
$f_{0}$
is subordinate to a starlike biholomorphic function in the unit disk
![]() $\mathbb {D}$
.
$\mathbb {D}$
.
Theorem 3.3 Let F be a polyanalytic function of order p in
![]() $\mathbb {D}$
with
$\mathbb {D}$
with
![]() $F(z)= \sum _{l=0}^{p-1} \overline {z}^l \, f_{l}(z) $
, where each
$F(z)= \sum _{l=0}^{p-1} \overline {z}^l \, f_{l}(z) $
, where each
![]() $f_{l}: \mathbb {D} \rightarrow \mathcal {B}(\mathcal {H})$
are analytic functions such that
$f_{l}: \mathbb {D} \rightarrow \mathcal {B}(\mathcal {H})$
are analytic functions such that
![]() $f_{l}(z)= \sum _{n=0}^{\infty } A_{n,l} z^n$
in
$f_{l}(z)= \sum _{n=0}^{\infty } A_{n,l} z^n$
in
![]() $\mathbb {D}$
and
$\mathbb {D}$
and
![]() $A_{n,l} \in \mathcal {B}(\mathcal {H})$
for
$A_{n,l} \in \mathcal {B}(\mathcal {H})$
for
![]() $n \in \mathbb {N} \cup \{0\}$
. Also, assume that:
$n \in \mathbb {N} \cup \{0\}$
. Also, assume that:
-
(1)
 $f_{0} \in S(g)$
such that
$f_{0} \in S(g)$
such that
 $f_{0}(0)=\mathbf {0}$
and
$f_{0}(0)=\mathbf {0}$
and
 $f^{\prime }_{l}(0)=\alpha _{l} f^{\prime }_{0}(0)$
with
$f^{\prime }_{l}(0)=\alpha _{l} f^{\prime }_{0}(0)$
with
 $|\alpha _{l}| <k$
for
$|\alpha _{l}| <k$
for
 $k \in [0,1]$
and each
$k \in [0,1]$
and each
 $l=1,\ldots , p-1$
, where
$l=1,\ldots , p-1$
, where
 $g:\mathbb {D} \rightarrow \mathcal {B}(\mathcal {H})$
is a normalized starlike biholomorphic function with
$g:\mathbb {D} \rightarrow \mathcal {B}(\mathcal {H})$
is a normalized starlike biholomorphic function with
 $g(z)= zI+\sum _{n=2}^{\infty } g_{n} z^n$
in
$g(z)= zI+\sum _{n=2}^{\infty } g_{n} z^n$
in
 $\mathbb {D}$
and
$\mathbb {D}$
and
 $g_{n} \in \mathcal {B}(\mathcal {H})$
for
$g_{n} \in \mathcal {B}(\mathcal {H})$
for
 $n \in \mathbb {N} \cup \{0\}$
.
$n \in \mathbb {N} \cup \{0\}$
. -
(2)
 $\omega _{l} : \mathbb {D} \rightarrow \mathcal {B}(\mathcal {H})$
is an analytic function with
$\omega _{l} : \mathbb {D} \rightarrow \mathcal {B}(\mathcal {H})$
is an analytic function with
 $\left \lVert \omega _{l}(z)\right \rVert \leq k$
in
$\left \lVert \omega _{l}(z)\right \rVert \leq k$
in
 $\mathbb {D}$
for
$\mathbb {D}$
for
 $k \in [0,1]$
, where
$k \in [0,1]$
, where
 $\omega _{l}(z)= f^{\prime }_{l}(z) (f^{\prime }_{0}(z))^{-1}$
in
$\omega _{l}(z)= f^{\prime }_{l}(z) (f^{\prime }_{0}(z))^{-1}$
in
 $\mathbb {D}$
such that
$\mathbb {D}$
such that
 $\omega _{l}(z)=\sum _{n=0}^{\infty } \omega _{n,l} z^n $
in
$\omega _{l}(z)=\sum _{n=0}^{\infty } \omega _{n,l} z^n $
in
 $\mathbb {D}$
.
$\mathbb {D}$
.
Then
![]() $M_{r}(F) \leq 1$
for
$M_{r}(F) \leq 1$
for
![]() $|z|=r \leq R_{S}= \min \{r_{S}(p,k), 1/3\}$
, where
$|z|=r \leq R_{S}= \min \{r_{S}(p,k), 1/3\}$
, where
![]() $r_{s}(p,k)$
is the smallest root in
$r_{s}(p,k)$
is the smallest root in
![]() $(0,1)$
of
$(0,1)$
of
Proof Let
![]() $g:\mathbb {D} \rightarrow \mathcal {B}(\mathcal {H})$
be a normalized starlike biholomorphic function. Then, in view of [Reference Graham and Kohr17, Theorem 6.2.6], g satisfies
$g:\mathbb {D} \rightarrow \mathcal {B}(\mathcal {H})$
be a normalized starlike biholomorphic function. Then, in view of [Reference Graham and Kohr17, Theorem 6.2.6], g satisfies
where
![]() $q:\mathbb {D} \rightarrow \mathbb {C}$
is an analytic function with
$q:\mathbb {D} \rightarrow \mathbb {C}$
is an analytic function with
![]() ${\operatorname {Re}\,} q(z)>0$
in
${\operatorname {Re}\,} q(z)>0$
in
![]() $\mathbb {D}$
and
$\mathbb {D}$
and
![]() $q(0)=1$
. By comparing the coefficients in the power series of both the sides of (3.21), we obtain
$q(0)=1$
. By comparing the coefficients in the power series of both the sides of (3.21), we obtain
By using induction and (3.22), we obtain
which turns out that
![]() $\left \lVert g_{n}\right \rVert \leq n$
for all
$\left \lVert g_{n}\right \rVert \leq n$
for all
![]() $n \geq 2$
. Since,
$n \geq 2$
. Since,
![]() $f_{0} \in S(g)$
, by using (3.19), for
$f_{0} \in S(g)$
, by using (3.19), for
![]() $r\leq 1/3$
, we obtain
$r\leq 1/3$
, we obtain
 $$ \begin{align} M_{r}(f_{0})=\sum_{n=1}^{\infty} \left\lVert A_{n,0}\right\rVert r^n \leq \sum_{n=1}^{\infty} \left\lVert g_{n}\right\rVert r^n \leq r+ \sum_{n=2}^{\infty} nr^n=\frac{r}{(1-r)^2}. \end{align} $$
$$ \begin{align} M_{r}(f_{0})=\sum_{n=1}^{\infty} \left\lVert A_{n,0}\right\rVert r^n \leq \sum_{n=1}^{\infty} \left\lVert g_{n}\right\rVert r^n \leq r+ \sum_{n=2}^{\infty} nr^n=\frac{r}{(1-r)^2}. \end{align} $$
It is known that, for
![]() $\Omega _{\gamma }=\mathbb {D}$
, i.e.,
$\Omega _{\gamma }=\mathbb {D}$
, i.e.,
![]() $\gamma =0$
, if
$\gamma =0$
, if
![]() $h:\mathbb {D} \rightarrow \mathcal {B}(\mathcal {H})$
is holomorphic, then we have
$h:\mathbb {D} \rightarrow \mathcal {B}(\mathcal {H})$
is holomorphic, then we have
![]() $\lambda _{\mathcal {H}} \leq 1$
(see [Reference Allu and Halder6]). From (3.17), we have
$\lambda _{\mathcal {H}} \leq 1$
(see [Reference Allu and Halder6]). From (3.17), we have
Then, from (3.16), (3.23), and (3.24), we obtain
 $$ \begin{align*} M_{r}(F) \leq k\, \frac{r}{(1-r)^2} \left(\frac{1-r^p}{1-r}\right)\,\,\,\, \mbox{for} \,\,\,\, r \leq \frac{1}{3}. \end{align*} $$
$$ \begin{align*} M_{r}(F) \leq k\, \frac{r}{(1-r)^2} \left(\frac{1-r^p}{1-r}\right)\,\,\,\, \mbox{for} \,\,\,\, r \leq \frac{1}{3}. \end{align*} $$
Hence,
![]() $M_{r}(F) \leq 1$
for
$M_{r}(F) \leq 1$
for
![]() $r \leq R_{S}= \min \{r_{S}(p,k), 1/3\}$
, where
$r \leq R_{S}= \min \{r_{S}(p,k), 1/3\}$
, where
![]() $r_{C}(p,k,\beta )$
is the smallest root in
$r_{C}(p,k,\beta )$
is the smallest root in
![]() $(0,1)$
of (3.20). This completes the proof.
$(0,1)$
of (3.20). This completes the proof.
Acknowledgment
The authors would like to express their sincerest gratitude to the referees for careful reading of the manuscript and many valuable suggestions, which greatly helped to improve the clarity of the exposition in this manuscript.
Competing interests
The authors declare none.