Article contents
Ergodic properties of invariant measures for C1+α non-uniformly hyperbolic systems
Published online by Cambridge University Press: 08 February 2012
Abstract
For every ergodic hyperbolic measure ω of a C1+α diffeomorphism, there is an ω-full-measure set 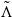 $\tilde {\Lambda }$ (the union of
$\tilde {\Lambda }$ (the union of 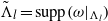 $\tilde \Lambda _l=\mathrm {supp}( \omega |_{\Lambda _{l}})$, the support sets of ω on each Pesin block Λl, l=1,2,…) such that every non-empty, compact and connected subset
$\tilde \Lambda _l=\mathrm {supp}( \omega |_{\Lambda _{l}})$, the support sets of ω on each Pesin block Λl, l=1,2,…) such that every non-empty, compact and connected subset 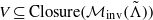 $V\subseteq \mathrm {Closure}(\mathcal {M}_{\mathrm {inv}}(\tilde \Lambda ))$ coincides with Vf(x), where
$V\subseteq \mathrm {Closure}(\mathcal {M}_{\mathrm {inv}}(\tilde \Lambda ))$ coincides with Vf(x), where 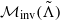 $\mathcal {M}_{\mathrm {inv}}(\tilde {\Lambda })$ denotes the space of invariant measures supported on
$\mathcal {M}_{\mathrm {inv}}(\tilde {\Lambda })$ denotes the space of invariant measures supported on 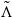 $\tilde {\Lambda }$ and Vf(x)denotes the accumulation set of time averages of Dirac measures supported at one orbit of some point x. For each fixed set V, the points with the above property are dense in the support supp (ω) . In particular, points satisfying
$\tilde {\Lambda }$ and Vf(x)denotes the accumulation set of time averages of Dirac measures supported at one orbit of some point x. For each fixed set V, the points with the above property are dense in the support supp (ω) . In particular, points satisfying  $V_f(x)=\mathrm {Closure}(\mathcal {M}_{\mathrm {inv}}(\tilde \Lambda ))$ are dense in supp (ω) . Moreover, if supp (ω)is isolated, the points satisfying
$V_f(x)=\mathrm {Closure}(\mathcal {M}_{\mathrm {inv}}(\tilde \Lambda ))$ are dense in supp (ω) . Moreover, if supp (ω)is isolated, the points satisfying  $V_f(x)\supseteq \mathrm {Closure}(\mathcal {M}_{\mathrm {inv}}(\tilde \Lambda ))$ form a residual subset of supp (ω) . These extend results of K. Sigmund [On dynamical systems with the specification property. Trans. Amer. Math. Soc. 190 (1974), 285–299] (see also M. Denker, C. Grillenberger and K. Sigmund [Ergodic Theory on Compact Spaces (Lecture Notes in Mathematics, 527). Springer, Berlin, Ch. 21]) from the uniformly hyperbolic case to the non-uniformly hyperbolic case. As a corollary, irregular + points form a residual set of supp (ω) .
$V_f(x)\supseteq \mathrm {Closure}(\mathcal {M}_{\mathrm {inv}}(\tilde \Lambda ))$ form a residual subset of supp (ω) . These extend results of K. Sigmund [On dynamical systems with the specification property. Trans. Amer. Math. Soc. 190 (1974), 285–299] (see also M. Denker, C. Grillenberger and K. Sigmund [Ergodic Theory on Compact Spaces (Lecture Notes in Mathematics, 527). Springer, Berlin, Ch. 21]) from the uniformly hyperbolic case to the non-uniformly hyperbolic case. As a corollary, irregular + points form a residual set of supp (ω) .
Information
- Type
- Research Article
- Information
- Copyright
- ©2012 Cambridge University Press
References
- 17
- Cited by

