Contents
Research Article
Bernoulli actions are weakly contained in any free action
-
- Published online by Cambridge University Press:
- 07 February 2012, pp. 323-333
-
- Article
- Export citation
Strong stochastic stability for non-uniformly expanding maps
-
- Published online by Cambridge University Press:
- 06 August 2012, pp. 647-692
-
- Article
- Export citation
Rational weak mixing in infinite measure spaces
-
- Published online by Cambridge University Press:
- 31 August 2012, pp. 1611-1643
-
- Article
- Export citation
Speedups of ergodic group extensions
-
- Published online by Cambridge University Press:
- 01 May 2012, pp. 969-982
-
- Article
- Export citation
Fatou–Julia theory for non-uniformly quasiregular maps
-
- Published online by Cambridge University Press:
- 16 December 2011, pp. 1-23
-
- Article
- Export citation
Dynamical systems of type
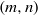 $(m,n)$ and their
$(m,n)$ and their 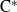 $\mathrm {C}^*$-algebras
$\mathrm {C}^*$-algebras
-
- Published online by Cambridge University Press:
- 27 July 2012, pp. 1291-1325
-
- Article
- Export citation
Ultraproducts of measure preserving actions and graph combinatorics
-
- Published online by Cambridge University Press:
- 16 February 2012, pp. 334-374
-
- Article
- Export citation
Hyperbolicity in the volume-preserving scenario
-
- Published online by Cambridge University Press:
- 23 August 2012, pp. 1644-1666
-
- Article
- Export citation
Local structure of self-affine sets
-
- Published online by Cambridge University Press:
- 06 September 2012, pp. 1326-1337
-
- Article
- Export citation
Lower and upper bounds for the Lyapunov exponents of twisting dynamics: a relationship between the exponents and the angle of Oseledets’ splitting
-
- Published online by Cambridge University Press:
- 17 April 2012, pp. 693-712
-
- Article
- Export citation
A local ergodic theorem for non-uniformly hyperbolic symplectic maps with singularities
-
- Published online by Cambridge University Press:
- 09 July 2012, pp. 983-1007
-
- Article
- Export citation
Maximizing points and coboundaries for an irrational rotation on a circle
-
- Published online by Cambridge University Press:
- 16 January 2012, pp. 24-48
-
- Article
- Export citation
On infinitely cohomologous to zero observables
-
- Published online by Cambridge University Press:
- 08 February 2012, pp. 375-399
-
- Article
- Export citation
Poisson approximation for the number of visits to balls in non-uniformly hyperbolic dynamical systems
-
- Published online by Cambridge University Press:
- 07 February 2012, pp. 49-80
-
- Article
- Export citation
Cubic critical portraits and polynomials with wandering gaps
-
- Published online by Cambridge University Press:
- 31 August 2012, pp. 713-738
-
- Article
- Export citation
On the selection of subaction and measure for a subclass of potentials defined by P. Walters
-
- Published online by Cambridge University Press:
- 04 July 2012, pp. 1338-1362
-
- Article
- Export citation
Equidistribution of joinings under off-diagonal polynomial flows of nilpotent Lie groups
-
- Published online by Cambridge University Press:
- 05 September 2012, pp. 1667-1708
-
- Article
- Export citation
A Fréchet law and an Erdős–Philipp law for maximal cuspidal windings
-
- Published online by Cambridge University Press:
- 18 July 2012, pp. 1008-1028
-
- Article
- Export citation
A survey on spectral multiplicities of ergodic actions
-
- Published online by Cambridge University Press:
- 09 December 2011, pp. 81-117
-
- Article
- Export citation
Internal perturbations of homoclinic classes: non-domination, cycles, and self-replication
-
- Published online by Cambridge University Press:
- 16 April 2012, pp. 739-776
-
- Article
- Export citation
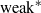
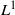
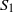
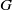
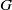
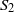
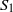
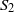

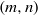
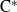

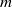

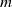
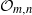

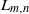
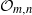
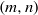
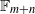
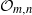

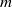
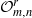
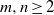
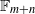
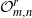
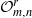
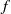
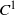
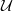
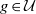
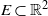

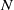

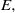
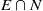
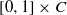
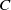
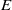
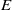
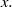
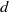
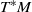
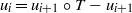
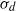
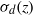
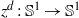
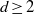
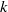
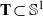
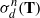
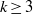
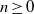
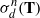
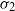
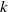
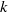
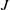
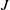
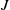
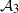
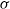
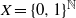
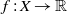
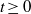
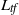
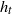
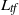
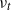
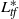
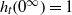
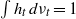
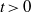
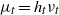
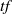
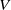
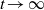
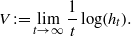
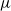
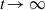
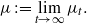
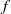
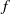
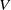
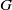
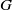
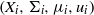
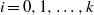
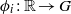
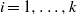
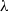
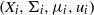
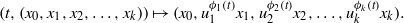
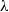
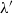
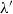
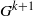
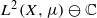 by
by  are realizable as ℳ(
are realizable as ℳ(