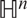 $\mathbb{H}^{{\it n}}$
$\mathbb{H}^{{\it n}}$Published online by Cambridge University Press: 21 January 2019
We investigate questions on the existence of nontrivial solution for a class of the critical Kirchhoff-type problems in Hyperbolic space. By the use of the stereographic projection the problem becomes a singular problem on the boundary of the open ball 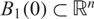 $B_1(0)\subset \mathbb{R}^n$ Combining a version of the Hardy inequality, due to Brezis–Marcus, with the mountain pass theorem due to Ambrosetti–Rabinowitz are used to obtain the nontrivial solution. One of the difficulties is to find a range where the Palais Smale converges, because our equation involves a nonlocal term coming from the Kirchhoff term.
$B_1(0)\subset \mathbb{R}^n$ Combining a version of the Hardy inequality, due to Brezis–Marcus, with the mountain pass theorem due to Ambrosetti–Rabinowitz are used to obtain the nontrivial solution. One of the difficulties is to find a range where the Palais Smale converges, because our equation involves a nonlocal term coming from the Kirchhoff term.