No CrossRef data available.
Published online by Cambridge University Press: 31 January 2019
We show that for any n and q, the number of real conjugacy classes in 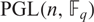 $ \rm{PGL}(\it{n},\mathbb{F}_q) $ is equal to the number of real conjugacy classes of
$ \rm{PGL}(\it{n},\mathbb{F}_q) $ is equal to the number of real conjugacy classes of 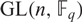 $ \rm{GL}(\it{n},\mathbb{F}_q) $ which are contained in
$ \rm{GL}(\it{n},\mathbb{F}_q) $ which are contained in 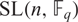 $ \rm{SL}(\it{n},\mathbb{F}_q) $, refining a result of Lehrer [J. Algebra36(2) (1975), 278–286] and extending the result of Gill and Singh [J. Group Theory14(3) (2011), 461–489] that this holds when n is odd or q is even. Further, we show that this quantity is equal to the number of real conjugacy classes in
$ \rm{SL}(\it{n},\mathbb{F}_q) $, refining a result of Lehrer [J. Algebra36(2) (1975), 278–286] and extending the result of Gill and Singh [J. Group Theory14(3) (2011), 461–489] that this holds when n is odd or q is even. Further, we show that this quantity is equal to the number of real conjugacy classes in 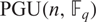 $ \rm{PGU}(\it{n},\mathbb{F}_q) $, and equal to the number of real conjugacy classes of
$ \rm{PGU}(\it{n},\mathbb{F}_q) $, and equal to the number of real conjugacy classes of 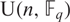 $ \rm{U}(\it{n},\mathbb{F}_q) $ which are contained in
$ \rm{U}(\it{n},\mathbb{F}_q) $ which are contained in 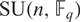 $ \rm{SU}(\it{n},\mathbb{F}_q) $, refining results of Gow [Linear Algebra Appl.41 (1981), 175–181] and Macdonald [Bull. Austral. Math. Soc.23(1) (1981), 23–48]. We also give a generating function for this common quantity.
$ \rm{SU}(\it{n},\mathbb{F}_q) $, refining results of Gow [Linear Algebra Appl.41 (1981), 175–181] and Macdonald [Bull. Austral. Math. Soc.23(1) (1981), 23–48]. We also give a generating function for this common quantity.