Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
1975.
Stochastic Convergence.
p.
191.

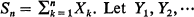 be independent random variables, each with mean zero and finite variance, and define
be independent random variables, each with mean zero and finite variance, and define 