Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-11T01:38:44.622Z Has data issue: false hasContentIssue false
  • English
  • Français

Disruption of turbulence due to particle loading in a dilute gas–particle suspension

Published online by Cambridge University Press:  26 February 2020

P. Muramulla Open the ORCID record for P. Muramulla [Opens in a new window] ,
A. Tyagi ,
P. S. Goswami Open the ORCID record for P. S. Goswami [Opens in a new window]  and
V. Kumaran Open the ORCID record for V. Kumaran [Opens in a new window]
P. Muramulla
Affiliation:
Department of Chemical Engineering, Indian Institute of Technology Bombay, Mumbai 400 076, India
A. Tyagi
Affiliation:
Department of Chemical Engineering, Indian Institute of Science, Bangalore 560 012, India
P. S. Goswami
Affiliation:
Department of Chemical Engineering, Indian Institute of Technology Bombay, Mumbai 400 076, India
V. Kumaran*
Affiliation:
Department of Chemical Engineering, Indian Institute of Science, Bangalore 560 012, India
*
†Email address for correspondence: kumaran@iisc.ac.in
Get access Rights & Permissions [Opens in a new window]

Abstract

The modification of fluid turbulence due to suspended particles is analysed using direct numerical simulations for the fluid turbulence and discrete particle simulations where the point-particle approximation is used for the particle force on the fluid. 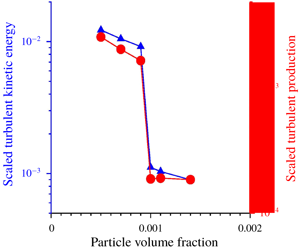Two values of the Reynolds number based on the channel width $h$ and the average gas velocity $\bar{u}$, $(\unicode[STIX]{x1D70C}_{f}\bar{u}h/\unicode[STIX]{x1D702}_{f})=3300$ and 5600 are considered, where $\unicode[STIX]{x1D70C}_{f}$ and $\unicode[STIX]{x1D702}_{f}$ are the gas density and viscosity. The particle Reynolds number based on the root mean square of the difference in the particle and fluid velocities is in the range 4–15. The particle volume fraction is small, in the range $0{-}3.5\times 10^{-3}$, the mass loading is varied in the range 0–13.5 and the particle Stokes number (ratio of particle relaxation time and fluid integral time) is varied in the range 1–420. Multiple models for the force on the particles are examined, the Stokes drag law, the Schiller–Naumann correlation, a correction to determine the ‘undisturbed’ fluid velocity at the particle centre, the lift force and wall corrections. In all cases, as the particle volume fraction is systematically increased, there is a discontinuous decrease in the turbulence intensities at a critical volume fraction. The mean square velocities and the rate of production of turbulent energy decrease by 1–2 orders of magnitude when the volume fraction is increased by $10^{-4}$ at the critical volume fraction. There is no compensatory increase in the particle fluctuating velocities or the energy dissipation rate due to the drag force on the particles, and there is a significant decrease in the total fluid energy dissipation rate at the critical volume fraction. This shows that the turbulence collapse is due to a catastrophic reduction in the turbulent energy production rate. This is contrary to the current understanding that turbulence attenuation is caused by the enhanced dissipation due to particle drag.

JFM classification

Multiphase and Particle-laden Flows: Particle/fluid flow Complex Fluids: Suspensions
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 889 , 25 April 2020 , A28
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Allen, M. P. & Tildesley, D. J. 2017 Computer Simulation of Liquids. Oxford University Press.CrossRefGoogle Scholar
Balachandar, S. 2009 A scaling analysis for point-particle approaches to turbulent multiphase flows. Intl J. Multiphase Flow 35 (9), 801–810.CrossRefGoogle Scholar
Balachandar, S. & Eaton, J. K. 2010 Turbulent dispersed multiphase flow. Annu. Rev. Fluid Mech. 42, 111–133.CrossRefGoogle Scholar
Balachandar, S. & Maxey, M. R. 1989 Methods for evaluating fluid velocities in spectral simulations of turbulence. J. Comput. Phys. 83, 96–125.CrossRefGoogle Scholar
Battista, F., Gualtieri, P., Mollicone, J.-P. & Casciola, C. M. 2018 Application of the exact regularised point particle method (ERPP) to particle laden turbulent shear flows in the two-way coupling regime. Intl J. Multiphase Flow 101, 113–124.CrossRefGoogle Scholar
Battista, F., Mollicone, J.-P., Gualtieri, P., Messina, R. & Casciola, C. M. 2019 Exact regularised point particle (ERPP) method for particle-laden wall-bounded flows in two-way coupling regime. J. Fluid Mech. 878, 420–444.CrossRefGoogle Scholar
Boivin, M., Simonin, O. & Squires, K. D. 1998 Direct numerical simulation of turbulence modulation by particles in isotropic turbulence. J. Fluid Mech. 375, 235–263.CrossRefGoogle Scholar
Canuto, C., Hussaini, M. & Zang, T. 1988 Spectral Methods in Fluid Dynamics. Springer.CrossRefGoogle Scholar
Canuto, C., Hussaini, M. Y., Quarteroni, A. & Zhang, T. A. 2007 Spectral Methods. Springer.CrossRefGoogle Scholar
Capecelatro, J., Desjardins, O. & Fox, R. O. 2015 On fluid–particle dynamics in fully developed cluster-induced turbulence. J. Fluid Mech. 780, 578–635.CrossRefGoogle Scholar
Capecelatro, J., Desjardins, O. & Fox, R. O. 2016 Strongly coupled fluid–particle flows in vertical channels. I. Reynolds-averaged two-phase turbulence statistics. Phys. Fluids 28, 033306.Google Scholar
Capecelatro, J., Desjardins, O. & Fox, R. O. 2018 On the transition between turbulence regimes in particle-laden channel flows. J. Fluid Mech. 845, 499–519.CrossRefGoogle Scholar
Cherukat, P., McLaughlin, J. B. & Graham, A. L. 1994 The inertial lift on a rigid sphere translating in a linear shear flow field. Intl J. Multiphase Flow 20 (2), 339–353.CrossRefGoogle Scholar
Costa, P., Brandt, L. & Picano, F. 2020 Interface-resolved simulations of small inertial particles in turbulent channel flow. J. Fluid Mech. 883, A54.CrossRefGoogle Scholar
Crowe, C. T. 1982 Numerical models for dilute gas–particle flows. Trans. ASME J. Fluids Engng 104 (3), 297–303.CrossRefGoogle Scholar
Dritselis, C. D. 2016 Direct numerical simulation of particle-laden turbulent channel flows with two- and four-way coupling effects: budgets of Reynolds stress and streamwise enstrophy. Fluid Dyn. Res. 48, 015507.Google Scholar
Elghobashi, S. & Truesdell, G. C. 1993 On the two-way interaction between homogeneous turbulence and dispersed solid particles. I. Turbulence modification. Phys. Fluids A 5 (7), 1790–1801.CrossRefGoogle Scholar
Esmaily, M. & Horwitz, J. A. K. 2018 A correction scheme for two-way coupled point-particle simulations on anisotropic grids. J. Comput. Phys. 375, 960–982.CrossRefGoogle Scholar
Fessler, J. R., Kulick, J. D. & Eaton, J. K. 1994 Preferential concentration of heavy particles in a turbulent channel flow. Phys. Fluids 6, 3742–3749.CrossRefGoogle Scholar
Garg, R., Narayanan, C., Lakehal, D. & Subramaniam, S. 2007 Accurate numerical estimation of interphase momentum transfer in Lagrangian–Eulerian simulations of dispersed two-phase flows. Intl J. Multiphase Flow 33, 1337–1364.CrossRefGoogle Scholar
Gibson, J. F., Halcrow, J. & Cvitanovi, P. 2008 Visualizing the geometry of state space in plane Couette flow. J. Fluid Mech. 611, 107–130.CrossRefGoogle Scholar
Gore, R. A. & Crowe, C. T. 1989 Effect of particle size on modulating turbulent intensity. Intl J. Multiphase Flow 15, 279.CrossRefGoogle Scholar
Goswami, P. S.2008 Particle dynamics in a turbulent particle–gas suspension at high Stokes number. PhD thesis, Indian Institute of Science, India.Google Scholar
Goswami, P. S. & Kumaran, V. 2010 Particle dynamics in a turbulent particle–gas suspension at high Stokes number. Part 1. Velocity and acceleration distributions. J. Fluid Mech. 646, 59–90.CrossRefGoogle Scholar
Goswami, P. S. & Kumaran, V. 2011a Particle dynamics in the channel flow of a turbulent particle–gas suspension at high Stokes number. Part 1. DNS and fluctuating force model. J. Fluid Mech. 687, 1–40.CrossRefGoogle Scholar
Goswami, P. S. & Kumaran, V. 2011b Particle dynamics in the channel flow of a turbulent particle–gas suspension at high Stokes number. Part 2. Comparison of fluctuating force simulations and experiments. J. Fluid Mech. 687, 41–71.CrossRefGoogle Scholar
Gualtieri, P., Battista, F. & Casciola, C. M. 2017 Turbulence modulation in heavy-loaded suspensions of tiny particles. Phys. Rev. Fluids 2, 034304.CrossRefGoogle Scholar
Hetsroni, G. 1989 Particle–turbulence interaction. Intl J. Multiphase Flow 15, 735.CrossRefGoogle Scholar
Hwang, W. & Eaton, J. K. 2006 Homogeneous and isotropic turbulence modulation by small heavy (St ∼ 50) particles. J. Fluid Mech. 564, 361–393.CrossRefGoogle Scholar
Kim, J., Moin, P. & Moser, R. 1987 Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 177, 133–166.CrossRefGoogle Scholar
Kleiser, L. & Schumann, U. 1980 Treatment of incompressibility and boundary conditions in 3-D numerical spectral simulations of plane channel flows. In Proceedings of the 3rd GAMM Conference on Numerical Methods in Fluid Mechanics, vol. 2, pp. 165–173. Vieweg.CrossRefGoogle Scholar
Kontomaris, K., Hanratty, T. J. & McLaughlin, J. B. 1992 An algorithm for tracking fluid particles in a spectral simulation of turbulent channel flow. J. Comput. Phys. 103, 231–242.CrossRefGoogle Scholar
Kulick, J. D., Fessler, J. R. & Eaton, J. K. 1994 Particle response and turbulence modification in a fully developed channel flow. J. Fluid Mech. 277, 109–134.CrossRefGoogle Scholar
Li, Y. & McLaughlin, J. B. 2001 Numerical simulation of particle-laden turbulent channel flow. Phys. Fluids 13, 2957.CrossRefGoogle Scholar
McLaughlin, J. B. 1989 Aerosol particle deposition in numerically simulated channel flow. Phys. Fluids A 1, 1211.CrossRefGoogle Scholar
McLaughlin, J. B. 1993 The lift on a small sphere in wall-bounded linear shear flows. J. Fluid Mech. 246, 249–265.CrossRefGoogle Scholar
Mehrabadi, M., Horwitz, J. A. K., Subramaniam, S. & Mani, A. 2018 A direct comparison of particle-resolved and point-particle methods in decaying turbulence. J. Fluid Mech. 850, 336–369.CrossRefGoogle Scholar
Naumann, Z. & Schiller, L. 1935 A drag coefficient correlation. Z. Verein. Deutsch. Ing. 77, 318–323.Google Scholar
Richter, D. H. 2015 Turbulence modification by inertial particles and its influence on the spectral energy budget in a planar Couette flow. Phys. Fluids 27, 063304.CrossRefGoogle Scholar
Rouson, D. W. I. & Eaton, J. K. 2001 On the preferential concentration of solid particles in turbulent channel flow. J. Fluid Mech. 428, 149.CrossRefGoogle Scholar
Saffman, P. G. T. 1965 The lift on a small sphere in a slow shear flow. J. Fluid Mech. 22 (2), 385–400.CrossRefGoogle Scholar
Squires, K. D. & Eaton, J. K. 1990 Particle response and turbulence modification in isotropic turbulence. Phys. Fluids A 2 (7), 1191–1203.CrossRefGoogle Scholar
Tanaka, T. & Eaton, J. K. 2008 Classification of turbulence modification by dispersed spheres using a novel dimensionless number. Phys. Rev. Lett. 101, 114502.CrossRefGoogle ScholarPubMed
Taneda, S. 1956 Experimental investigation of the wake behind a sphere at low Reynolds numbers. J. Phys. Soc. Japan 11, 1104–1108.CrossRefGoogle Scholar
Tyagi, A.2017 Direct numerical simulations and fluctuating force simulations of a turbulent gas–particle suspension. PhD thesis, Indian Institute of Science, India.Google Scholar
Vreman, A. W. 2015 Turbulence attenuation in particle-laden flow in smooth and rough channels. J. Fluid Mech. 773, 103–136.CrossRefGoogle Scholar
Vreman, B., Geurts, B. J., Deen, N. G., Kuipers, J. A. M. & Kuerten, J. G. M. 2009 Two-and four-way coupled Euler–Lagrangian large-eddy simulation of turbulent particle-laden channel flow. Flow Turbul. Combust. 82 (1), 47–71.CrossRefGoogle Scholar
Wang, G., Fong, K. E., Coletti, F., Capecelatro, J. & Richter, D. H. 2019 Inertial particle velocity and distribution in vertical turbulent channel flow: a numerical and experimental comparison. Intl J. Multiphase Flow 120, 103105.Google Scholar
Wang, G. & Richter, D. H. 2019 Modulation of the turbulence regeneration cycle by inertial particles in planar Couette flow. J. Fluid Mech. 861, 901–929.CrossRefGoogle Scholar
Wang, Q., Squires, K. D., Chen, M. & McLaughlin, J. B. 1997 On the role of the lift force in turbulence simulations of particle deposition. Intl J. Multiphase Flow 23 (4), 749–763.CrossRefGoogle Scholar
Yamamoto, Y., Potthoff, M., Tanaka, T., Kajishima, T. & Tsuji, Y. 2001 Large-eddy simulation of turbulent gas–particle flow in a vertical channel: effect of considering interparticle collisions. J. Fluid Mech. 442, 303–334.CrossRefGoogle Scholar
Yeung, P. K. & Pope, S. B. 1988 An algorithm for tracking fluid particles in numerical simulation of homogeneous turbulence. J. Comput. Phys. 79, 373–416.CrossRefGoogle Scholar
Zang, T. A. 1991 On the rotation and skew-symmetric forms for incompressible flow simulations. Appl. Numer. Maths 7, 27–40.CrossRefGoogle Scholar
Zeng, L., Najjar, F., Balachandar, S. & Fischer, P. 2009 Forces on a finite-sized particle located close to a wall in a linear shear flow. Phys. Fluids 21 (3), 033302.CrossRefGoogle Scholar
Zhang, H. & Ahmadi, G. 2000 Aerosol particle transport and deposition in vertical and horizontal turbulent duct flows. J. Fluid Mech. 406, 55–80.CrossRefGoogle Scholar