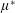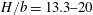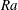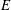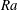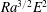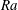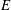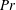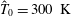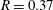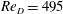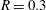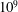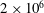JFM Rapids
Effect of aspect ratio on vertical-axis wind turbine wakes
-
- Published online by Cambridge University Press:
- 21 February 2020, R1
-
- Article
- Export citation
Onset of Darcy–Bénard convection under throughflow of a shear-thinning fluid
-
- Published online by Cambridge University Press:
- 21 February 2020, R2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
An efficient cellular flow model for cohesive particle flocculation in turbulence
-
- Published online by Cambridge University Press:
- 24 February 2020, R3
-
- Article
- Export citation
JFM Papers
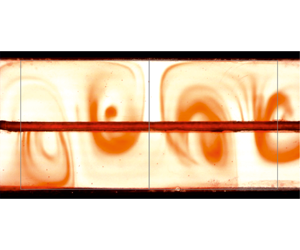
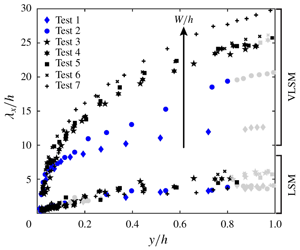
On the scaling of large-scale structures in smooth-bed turbulent open-channel flows
-
- Published online by Cambridge University Press:
- 18 February 2020, A1
-
- Article
- Export citation
Acoustic streaming in turbulent compressible channel flow for heat transfer enhancement
-
- Published online by Cambridge University Press:
- 18 February 2020, A2
-
- Article
- Export citation
Steady detonation propagation in thin channels with strong confinement
-
- Published online by Cambridge University Press:
- 18 February 2020, A3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the near-field interfaces of homogeneous and immiscible round turbulent jets
-
- Published online by Cambridge University Press:
- 18 February 2020, A4
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Preasymptotic Taylor dispersion: evolution from the initial condition
-
- Published online by Cambridge University Press:
- 20 February 2020, A5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Heat and momentum transfer to a particle in a laminar boundary layer
-
- Published online by Cambridge University Press:
- 24 February 2020, A6
-
- Article
- Export citation
Scaling behaviour in spherical shell rotating convection with fixed-flux thermal boundary conditions
-
- Published online by Cambridge University Press:
- 21 February 2020, A7
-
- Article
- Export citation
A momentum-conserving wake superposition method for wind farm power prediction
-
- Published online by Cambridge University Press:
- 24 February 2020, A8
-
- Article
- Export citation
Shape optimization of tumbling wings
-
- Published online by Cambridge University Press:
- 21 February 2020, A9
-
- Article
- Export citation
On non-Oberbeck–Boussinesq effects in Rayleigh–Bénard convection of air for large temperature differences
-
- Published online by Cambridge University Press:
- 21 February 2020, A10
-
- Article
- Export citation
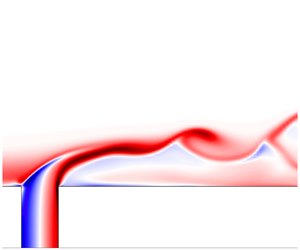
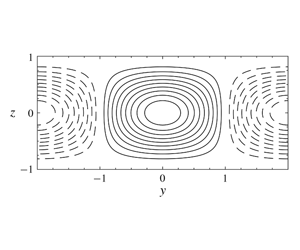
Time-dependent Kelvin cat-eye structure due to current–topography interaction
-
- Published online by Cambridge University Press:
- 24 February 2020, A11
-
- Article
- Export citation
Global linear analysis of a jet in cross-flow at low velocity ratios
-
- Published online by Cambridge University Press:
- 21 February 2020, A12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Streamwise-constant large-scale structures in Couette and Poiseuille flows
-
- Published online by Cambridge University Press:
- 21 February 2020, A13
-
- Article
- Export citation
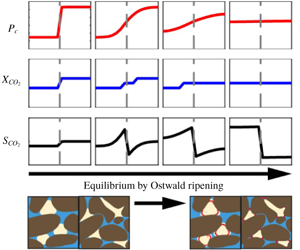
A continuum-scale representation of Ostwald ripening in heterogeneous porous media
-
- Published online by Cambridge University Press:
- 21 February 2020, A14
-
- Article
- Export citation
Liquid plug formation from heated binary mixtures in capillary tubes
-
- Published online by Cambridge University Press:
- 24 February 2020, A15
-
- Article
- Export citation
Falling film with insoluble surfactants: effects of surface elasticity and surface viscosities
-
- Published online by Cambridge University Press:
- 21 February 2020, A16
-
- Article
- Export citation
Self-similar pressure-atomized sprays
-
- Published online by Cambridge University Press:
- 21 February 2020, A17
-
- Article
- Export citation