No CrossRef data available.
Article contents
Ideal and non-ideal planar compressible fluid flows in radial equilibrium
Published online by Cambridge University Press: 22 November 2023
Abstract
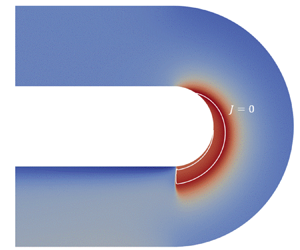
Two-dimensional compressible flows in radial equilibrium are investigated in the ideal dilute-gas regime and the non-ideal single-phase regime close to the liquid–vapour saturation curve and the critical point. Radial equilibrium flows along constant-curvature streamlines are considered. All properties are therefore independent of the tangential streamwise coordinate. A differential relation for the Mach number dependency on the radius is derived for both ideal and non-ideal conditions. For ideal flows, the differential relation is integrated analytically. Assuming a constant specific heat ratio  $\gamma$, the Mach number is a monotonically decreasing function of the radius of curvature for ideal flows, with
$\gamma$, the Mach number is a monotonically decreasing function of the radius of curvature for ideal flows, with  $\gamma$ being the only fluid-dependent parameter. In non-ideal conditions, the Mach number profile also depends on the total thermodynamic conditions of the fluid. For high molecular complexity fluids, such as toluene or hexamethyldisiloxane, a non-monotone Mach number profile is admissible in single-phase supersonic conditions. For Bethe–Zel'dovich–Thompson fluids, non-monotone behaviour is observed in subsonic conditions. Numerical simulations of subsonic and supersonic turning flows are carried out using the streamline curvature method and the computational fluid dynamics software SU2, respectively, both confirming the flow evolution from uniform flow conditions to the radial equilibrium profile predicted by the theory.
$\gamma$ being the only fluid-dependent parameter. In non-ideal conditions, the Mach number profile also depends on the total thermodynamic conditions of the fluid. For high molecular complexity fluids, such as toluene or hexamethyldisiloxane, a non-monotone Mach number profile is admissible in single-phase supersonic conditions. For Bethe–Zel'dovich–Thompson fluids, non-monotone behaviour is observed in subsonic conditions. Numerical simulations of subsonic and supersonic turning flows are carried out using the streamline curvature method and the computational fluid dynamics software SU2, respectively, both confirming the flow evolution from uniform flow conditions to the radial equilibrium profile predicted by the theory.
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press


