Published online by Cambridge University Press: 27 December 2019
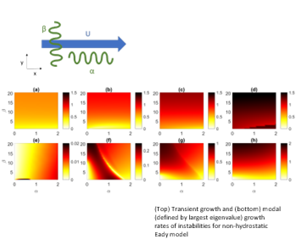
The problem of optimal initial disturbances in thermal wind shear is revisited and extended to include non-hydrostatic effects. This systematic study compares transient and modal growth rates of submesoscale instabilities over a large range of zonal and meridional wavenumbers, aspect ratios and different Richardson number regimes. Selection criteria were derived to remove spurious and unresolved instability modes that arise from the eigenvalue problem and we generalize the study of the hydrostatic Eady problem by Heifetz & Farrell (J. Atmos. Sci., vol. 60, 2003; J. Atmos. Sci., vol. 64 (12), 2007, pp. 4366–4382; Q. J. R. Meteorol. Soc., vol. 134 (635), 2008, pp. 1627–1633) to thin fronts, characterized by large aspect ratios. Such fronts are commonly found at the early stages of frontogenesis, for example, in the ocean mesoscale eddies and near the eye wall of hurricanes. In particular, we show that transient energy growth rates are up to two orders of magnitude larger than modal counterparts for a wide range of Richardson number and that the effects of transient energy gain become even greater when non-hydrostatic effects become important and/or for large Richardson numbers. This study also compares the dominant energy pathways contributing to the energy growth at short and long times. For symmetric modes, we recover the inertia–gravity instability described in Xu et al. (J. Atmos. Sci., vol. 64 (6), 2007, pp. 1764–1781). These mechanisms are shown to be the most powerful mediator of vertical transport when compared with the fastest growing baroclinic and symmetric modes. These results highlight the importance of transient processes in the ocean and the atmosphere.
Please note a has been issued for this article.