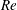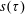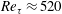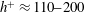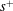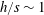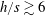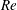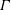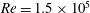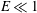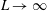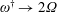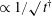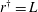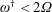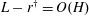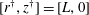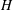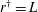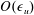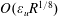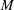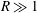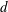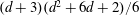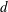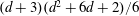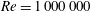JFM Rapids
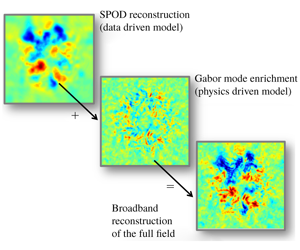
Broadband reconstruction of inhomogeneous turbulence using spectral proper orthogonal decomposition and Gabor modes
-
- Published online by Cambridge University Press:
- 06 February 2020, R1
-
- Article
- Export citation
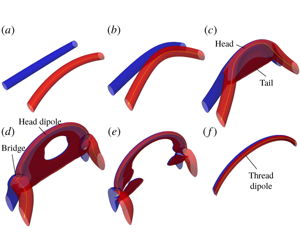
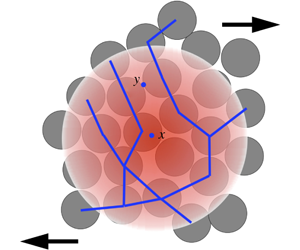
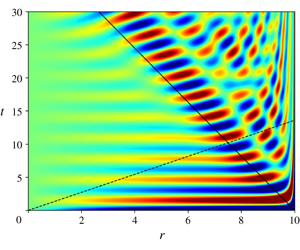
On singularity formation via viscous vortex reconnection
-
- Published online by Cambridge University Press:
- 06 February 2020, R2
-
- Article
- Export citation
A non-local constitutive model for slow granular flow that incorporates dilatancy
-
- Published online by Cambridge University Press:
- 17 February 2020, R3
-
- Article
- Export citation
Focus on Fluids
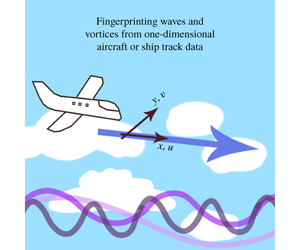
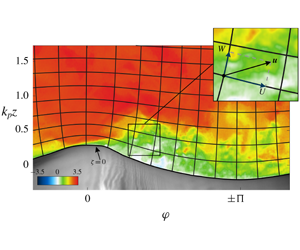
Untangling waves and vortices in the atmospheric kinetic energy spectra
-
- Published online by Cambridge University Press:
- 06 February 2020, F1
-
- Article
-
- You have access
- HTML
- Export citation
JFM Papers
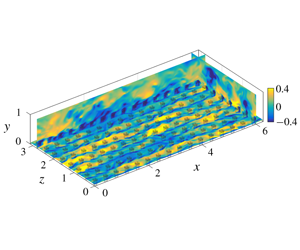
Scaling and dynamics of turbulence over sparse canopies
-
- Published online by Cambridge University Press:
- 06 February 2020, A1
-
- Article
- Export citation
Turbulent flows over dense filament canopies
-
- Published online by Cambridge University Press:
- 06 February 2020, A2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
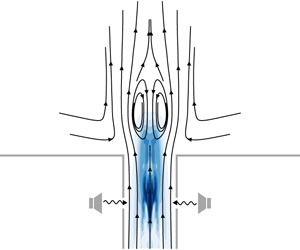
Receptivity of the turbulent precessing vortex core: synchronization experiments and global adjoint linear stability analysis
-
- Published online by Cambridge University Press:
- 06 February 2020, A3
-
- Article
- Export citation
Bypass transition in boundary layers subject to strong pressure gradient and curvature effects
-
- Published online by Cambridge University Press:
- 06 February 2020, A4
-
- Article
- Export citation
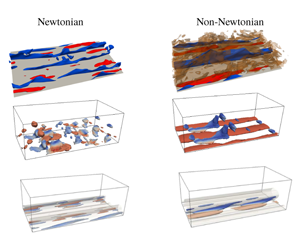
Coherent structures in the turbulent channel flow of an elastoviscoplastic fluid
-
- Published online by Cambridge University Press:
- 06 February 2020, A5
-
- Article
- Export citation
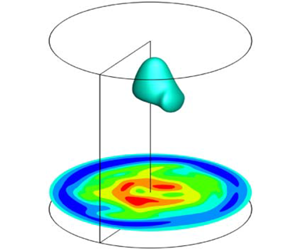
On the correlation between vortex breakdown bubble and planar helicity in Vogel–Escudier flow
-
- Published online by Cambridge University Press:
- 06 February 2020, A6
-
- Article
- Export citation
Entrainment of sediment particles by very large-scale motions
-
- Published online by Cambridge University Press:
- 06 February 2020, A7
-
- Article
- Export citation
Interactions of large-scale structures in the near field of round jets at high Reynolds numbers
-
- Published online by Cambridge University Press:
- 06 February 2020, A8
-
- Article
- Export citation
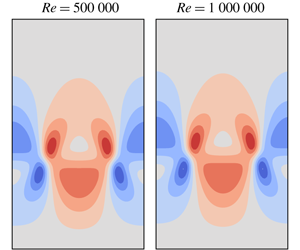
On the inertial wave activity during spin-down in a rapidly rotating penny shaped cylinder: a reduced model
-
- Published online by Cambridge University Press:
- 06 February 2020, A9
-
- Article
- Export citation
Generation of first Mack modes in supersonic boundary layers by slow acoustic waves interacting with streamwise isolated wall roughness
-
- Published online by Cambridge University Press:
- 06 February 2020, A10
-
- Article
- Export citation
Boundary layer formulations in orthogonal curvilinear coordinates for flow over wind-generated surface waves
-
- Published online by Cambridge University Press:
- 06 February 2020, A11
-
- Article
- Export citation
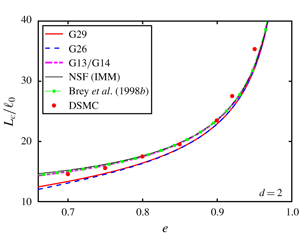
Moment theories for a $d$-dimensional dilute granular gas of Maxwell molecules
-
- Published online by Cambridge University Press:
- 06 February 2020, A12
-
- Article
- Export citation
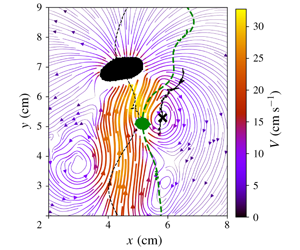
Interaction of two oscillating bubbles rising in a thin-gap cell: vertical entrainment and interaction with vortices
-
- Published online by Cambridge University Press:
- 06 February 2020, A13
-
- Article
- Export citation
Multifractal analysis of flame dynamics during transition to thermoacoustic instability in a turbulent combustor
-
- Published online by Cambridge University Press:
- 06 February 2020, A14
-
- Article
- Export citation
Self-similar invariant solution in the near-wall region of a turbulent boundary layer at asymptotically high Reynolds numbers
-
- Published online by Cambridge University Press:
- 07 February 2020, A15
-
- Article
- Export citation
Hydrodynamic ejection caused by laser-induced optical breakdown
-
- Published online by Cambridge University Press:
- 07 February 2020, A16
-
- Article
- Export citation