Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-27T05:27:06.844Z Has data issue: false hasContentIssue false
  • English
  • Français

Uniform bounds for norms of theta series and arithmetic applications

Part of: Additive number theory; partitions Multiplicative number theory Forms and linear algebraic groups Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  28 February 2022

FABIAN WAIBEL
FABIAN WAIBEL*
Affiliation:
Department of Mathematics, University of Bonn, Endenicher Allee 60, 53115 Bonn, Germany. e-mails: waibel@math.uni-bonn.de
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove uniform bounds for the Petersson norm of the cuspidal part of the theta series. This gives an improved asymptotic formula for the number of representations by a quadratic form. As an application, we show that every integer 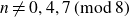$n \neq 0,4,7 \,(\textrm{mod}\ 8)$ is represented as 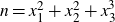$n= x_1^2 + x_2^2 + x_3^3$ for integers 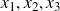$x_1,x_2,x_3$ such that the product 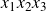$x_1x_2x_3$ has at most 72 prime divisors.

MSC classification

Primary: 11E25: Sums of squares and representations by other particular quadratic forms 11F30: Fourier coefficients of automorphic forms 11P05: Waring's problem and variants 11N37: Asymptotic results on arithmetic functions
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 173 , Issue 3 , November 2022 , pp. 669 - 691
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Cambridge Philosophical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Blomer, V., Uniform bounds for Fourier coefficients of theta-series with arithmetic applications, Acta Arith. 114 (2004), no. 1, 1–21.CrossRefGoogle Scholar
Blomer, V., Ternary quadratic forms, and sums of three squares with restricted variables, CRM Proceedings and Lecture Notes (American Mathematical Society, 2008), pp. 1–17.Google Scholar
Blomer, V. and Brüdern, J., A three squares theorem with almost primes, Bull. Lond. Math. Soc. 37 (2005), no. 4, 507–513.CrossRefGoogle Scholar
Blomer, V., Brüdern, J., and Dietmann, R., Sums of smooth squares, C. Math. 145 (2009), no. 6, 1401–1441.CrossRefGoogle Scholar
Blomer, V. and Pohl, A., The sup-norm problem on the Siegel modular space of rank two, Amer. J. Math. 138 (2016), no. 4, 999–1027.CrossRefGoogle Scholar
Browning, T. D. and Dietmann, R., On the representation of integers by quadratic forms, Proc. Lond. Math. Soc. 96 (2007), no. 2, 389–416.CrossRefGoogle Scholar
Cai, Y., Gauss’s three squares theorem involving almost-primes, Rocky Mountain J. Math. 42 (2012), no. 4, 1115–1134.CrossRefGoogle Scholar
Cassels, J.W.S., Rational quadratic forms, London Math. Soc. Monogr. vol. 13 (Academic Press, 1978).Google Scholar
Ching, T. W., Lagrange’s equation with one prime and three almost-primes, J. Number Theory 183 (2018), 442–465.CrossRefGoogle Scholar
Diamond, H. and Halberstam, H., Some applications of sieves of dimension exceeding 1. Sieve Methods, Exponential Sums and their Applications in Number Theory (Cambridge University Press, 1997), pp. 101–108.CrossRefGoogle Scholar
Duke, W., On ternary quadratic forms, J. Number Theory 110 (2005), no. 1, 37–43.CrossRefGoogle Scholar
Fomenko, O. M., Estimates of Petersson’s inner squares of cusp forms and arithmetic applications, Journal of Soviet Mathematics 53 (1991), no. 3, 323–338.CrossRefGoogle Scholar
Gradshteyn, I. S. and Ryzhik, I. M., Table of Integrals, Series, and Products, 7th ed. (Academic Press, New York, 2007).Google Scholar
Halberstam, H. and Richert, H.-E., Sieve Methods (Academic Press, New York, 1974).Google Scholar
Hanke, J., Local densities and explicit bounds for representability by a quadratic form, Duke Math. J. 124 (2004), no. 2, 351–388.CrossRefGoogle Scholar
Hsia, J. and Icaza, M., Effective version of Tartakowsky’s theorem, Acta Arith. 89 (1999), no. 3, 235–253.CrossRefGoogle Scholar
Iwaniec, H., Fourier coefficients of modular forms of half-integral weight., Invent. Math. 87 (1987), 385–402.CrossRefGoogle Scholar
Iwaniec, H. and Kowalski, E., Analytic number theory, Colloquium Publications, vol. 53 (American Mathematical Society, 2004).CrossRefGoogle Scholar
Jones, Burton W., The arithmetic theory of quadratic forms, 1 ed., The Carus Mathematical Monographs, vol. 10 (Mathematical Association of America, 1950).Google Scholar
Lü, G., Gauss’s three squares theorem with almost prime variables, Acta Arith. 128 (2007), no. 4, 391–399.CrossRefGoogle Scholar
O’Meara, O.T., Introduction to quadratic forms. Grundlehren Math. Wiss., vol. 117 (Springer, New York, 1973).Google Scholar
Rouse, J., Quadratic forms representing all odd positive integers, Amer. J. Math. 136 (2014), no. 6, 1693–1745.CrossRefGoogle Scholar
Rouse, J., Integers represented by positive-definite quadratic forms and Petersson inner products, Acta Arith. 187 (2019), 81–100.Google Scholar
Sardari, N. T., Quadratic forms and semiclassical eigenfunction hypothesis for flat tori, Comm. Math. Phys. 358 (2018), 895–917.CrossRefGoogle Scholar
Schulze–Pillot, R., On explicit versions of Tartakovski’s theorem, Arch. Math. (Basel) 77 (2001), no. 2, 129–137.CrossRefGoogle Scholar
Schulze–Pillot, R. and Yenirce, A., Petersson products of bases of spaces of cusp forms and estimates for Fourier coefficients, Int. J. Number Theory 14 (2018), no. 8, 2277–2290.CrossRefGoogle Scholar
Siegel, C. L., Über die analytische Theorie der quadratischen Formen, Ann. of Math. 36 (1935), no. 3, 527–600.CrossRefGoogle Scholar
Tartakowsky, W., Die Gesamtheit der Zahlen, die durch eine positive quadratische Form $f(x_1, . . . , x_s) (s \geq 4)$ darstellbar sind, Izv. Akad. Nauk SSSR 7 (1929), no. 1, 111–121.Google Scholar
Tsang, K.-M. and Zhao, L., On Lagrange’s four squares theorem with almost prime variables. J. Reine Angew Math. 2017 (2017), no. 726, 129–171.CrossRefGoogle Scholar
Waibel, F., Fourier coefficients of half-integral weight cusp forms and Waring’s problem, Ramanujan J. 47 (2017), no. 1, 185–200.CrossRefGoogle Scholar
Watson, G. L., Integral Quadratic Forms, Cambridge Tracts in Math. Theoret. Phys. vol. 51 (Cambridge University Press, New York, 1960).Google Scholar
Yang, T., An explicit formula for local densities of quadratic forms, J. Number Theory 72 (1998), no. 2, 309–356.CrossRefGoogle Scholar