No CrossRef data available.
Published online by Cambridge University Press: 24 October 2008
In the classical theory (3) due to Knopp, Agnew and others, the core K(x) of a sequence x = {ξn} of complex numbers is defined by 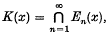 where En(x) is the smallest closed convex set containing all ξk with k ≥ n. A matrix transformation T is said to be a core-preserving transformation if
where En(x) is the smallest closed convex set containing all ξk with k ≥ n. A matrix transformation T is said to be a core-preserving transformation if

holds for all sequences x. T is core-preserving for bounded sequences if (1·1) holds for all bounded sequences x. It is readily proved that K(x) is the set of complex numbers ζ such that
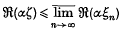
for all complex numbers α (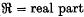 ). Now
). Now 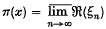 is a sub-additive, positive-homogeneous real-valued functional defined on the vector space of bounded complex sequences. This suggests the construction of an abstract theory on the following lines.
is a sub-additive, positive-homogeneous real-valued functional defined on the vector space of bounded complex sequences. This suggests the construction of an abstract theory on the following lines.