Research Article
Algebras which represent their linear functionals
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 1-14
-
- Article
- Export citation
On multiplicative systems defined by generators and relations: II. Monogenic loops
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 579-589
-
- Article
- Export citation
Ordinal recursion
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 175-182
-
- Article
- Export citation
A formalization of an ℵ0-valued propositional calculus
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 367-376
-
- Article
- Export citation
Two theorems on Engel groups
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 377-380
-
- Article
- Export citation
Bounded-weak topologies and completeness in vector spaces
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 183-189
-
- Article
- Export citation
Commutators in associative rings
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 590-594
-
- Article
- Export citation
Core-preserving transformations of a vector space
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 15-25
-
- Article
- Export citation
The codifying of tree-structure
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 381-385
-
- Article
- Export citation
Triangular representations of linear algebras
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 595-600
-
- Article
- Export citation
On closest packing by equilateral triangles
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 26-30
-
- Article
- Export citation
On the product of n linear forms
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 190-193
-
- Article
- Export citation
On approximate solutions of linear differential equations
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 601-611
-
- Article
- Export citation
The Hausdorff α-dimensional measure of Brownian paths in n-space
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 31-39
-
- Article
- Export citation
An irreducible non-convex region
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 194-200
-
- Article
- Export citation
Some results concerning the local analytic branches of an algebraic variety
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 386-396
-
- Article
- Export citation
On eigenvalues and inverse singular values of compact linear operators in Hilbert space
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 201-212
-
- Article
- Export citation
On measure of sum sets II. The sum-theorem for the torus
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 40-43
-
- Article
- Export citation
On the evaluation of the confluent hypergeometric function
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 612-622
-
- Article
- Export citation
Hyperelliptic threefolds
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 397-409
-
- Article
- Export citation

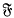 and let π(
and let π(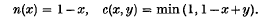
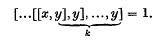
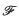 is
is 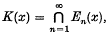 where
where 
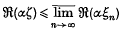
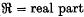 ). Now
). Now 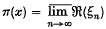 is a sub-additive, positive-homogeneous real-valued functional defined on the vector space of bounded complex sequences. This suggests the construction of an abstract theory on the following lines.
is a sub-additive, positive-homogeneous real-valued functional defined on the vector space of bounded complex sequences. This suggests the construction of an abstract theory on the following lines.
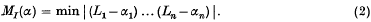

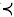 . That ís to say, there is just one star domain
. That ís to say, there is just one star domain 
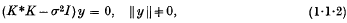
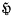 ,
,