Cushions, cigars and diamonds: an area-perimeter problem for symmetric ovals

Extract

P. R. Scott (1) has asked which two-dimensional closed convex set E, centro-symmetric in the origin O, and containing no other Cartesian lattice-point in its interior, maximizes the ratio A/P, where A, P are the area, perimeter of E; he conjectured that the answer is the ‘rounded square’ (‘cushion’ in what follows), described below. We shall prove this, indeed in a more general setting, by seeking to maximize

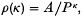
where κ is a parameter (0 < κ < 2); the set of admissible E is those E centro-symmetric in 0 that do not contain in their interior certain fixed lattice-points. There are two problems, the unrestricted one 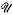, where there is no given upper bound on A (it will become apparent that this problem only has a finite answer when κ ≥ 1) and the restricted one 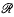, when one is given a bound B and we must have A ≤ B. Special interest attaches to the case B = 4, both because of Minkowski's theorem: any E symmetric in O and containing no other lattice-point has area at most 4; and because it turns out that it is a ‘natural’ condition: the algebraic expressions simplify to a remarkable extent. Hence in what follows, the ‘restricted case 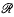’ shall mean A ≤ 4.