Research Article
Affine cubic functions: I. The complex plane
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 387-401
-
- Article
- Export citation
Cushions, cigars and diamonds: an area-perimeter problem for symmetric ovals
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 1-16
-
- Article
- Export citation
Universal matrices
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 193-198
-
- Article
- Export citation
Quaternionic analysis
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 199-225
-
- Article
- Export citation
Note on the invariant of plane cubics
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 403-406
-
- Article
- Export citation
On triangle contractive operators in Hilbert spaces
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 17-20
-
- Article
- Export citation
The modular curve X0(39) and rational isogeny
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 21-23
-
- Article
- Export citation
Algebraic solutions of partizan games with cycles
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 227-246
-
- Article
- Export citation
The probability that a point of a tree is fixed
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 407-415
-
- Article
- Export citation
Embedding theorems for groups with an integer-valued length function
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 417-429
-
- Article
- Export citation
Augmentation quotients of group rings and symmetric powers
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 247-252
-
- Article
- Export citation
The arithmetic plurigenera of surfaces
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 25-31
-
- Article
- Export citation
Closure operations for Schunck classes and formations of finite solvable groups
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 253-259
-
- Article
- Export citation
On Grothendieck's local duality theorem
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 431-437
-
- Article
- Export citation
Intersection multiplicities and tangent cones
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 33-42
-
- Article
- Export citation
Stratifying jet spaces – some special cases
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 439-444
-
- Article
- Export citation
Augmentation quotients of some nonabelian finite groups
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 261-270
-
- Article
- Export citation
An application of p-factorization methods to symmetric graphs
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 43-48
-
- Article
- Export citation
Representations and automorphisms of some wreath products
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 49-53
-
- Article
- Export citation
The covariance algebra of an extended covariant system
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 271-280
-
- Article
- Export citation

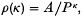
 , where there is no given upper bound on
, where there is no given upper bound on  , when one is given a bound
, when one is given a bound 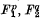 and
and 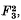 which are thus linearly dependent. The ring of all (relatively) invariant polynomials is generated by
which are thus linearly dependent. The ring of all (relatively) invariant polynomials is generated by 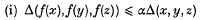
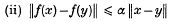
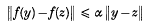
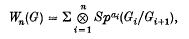
 and
and 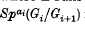 is the
is the 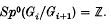
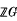 , the group ring of
, the group ring of 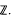 . Define the additive group
. Define the additive group 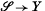 say, with fibre ρ
say, with fibre ρ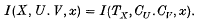
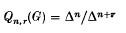
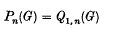
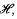 , and let
, and let 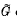 of
of 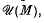 , the unitary group of
, the unitary group of 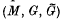 satisfies an additional axiom, we say that it is an extended covariant system. We define a Hilbert space
satisfies an additional axiom, we say that it is an extended covariant system. We define a Hilbert space 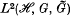 and operators
and operators 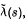 , acting on
, acting on  . The von Neumann algebra
. The von Neumann algebra 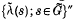 is then the covariance algebra of the extended covariant system
is then the covariance algebra of the extended covariant system 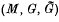 , denoted by
, denoted by 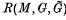 .
.