Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-27T10:46:06.781Z Has data issue: false hasContentIssue false
  • English
  • Français

The lattice properties of asymmetric hyperbolic regions

I. On a theorem of khintchine

Published online by Cambridge University Press:  24 October 2008

J. W. S. Cassels
J. W. S. Cassels
Affiliation:
Trinity CollegeCambridge
Get access Rights & Permissions [Opens in a new window]

Extract

Let θ > 0 and α ≠ 0 be real numbers, and let θ be irrational. Khintchine has shown, by the use of continued fractions, that there is an infinite number of pairs of positive integers (p, q) which satisfy the inequality

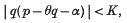
for any given K > 5−½; and, more recently, Jogin has shown the same is still true with K = 5−½. The condition that p and q shall be positive is, of course, essential, as otherwise there is the classical result K = ¼ due to Minkowski.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 44 , Issue 1 , January 1948 , pp. 1 - 7
Copyright
Copyright © Cambridge Philosophical Society 1948

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

* Khintchine, A., Math. Ann. 111 (1935), 631–7.CrossRefGoogle Scholar

† Jogin, I. I., Uchenye Zapiski Moskov Gos. Univ. Matematika, 73 (1944), 37–40;Google Scholar as quoted in Math. Rev. 7 (1946), 274.Google Scholar

‡ This has recently been improved by Khintchine, , Bull. Acad. Sci. U.R.S.S. 10 (1946), 281–93.Google Scholar Khintchine's results are easily proved by my present methods, and in a subsequent paper of this series I shall show how they can be both generalized and sharpened.

* Hurwitz, , Math. Ann. 39 (1891), 279–81.CrossRefGoogle Scholar See also Hardy, G. H. and Wright, E. M., An Introduction to the Theory of Numbers (Oxford, First edition, 1938; Second edition, 1945),Google Scholar § 11·8. We shall quote this book as Hardy-Wright.

† Hardy-Wright, § 11·10. Koksma, J. F., ‘Diophantische Approximationen’, Ergebn. Math. 4, no. 4 (Springer, Berlin, 1936), pp. 29Google Scholar et.seq.

* A. Khintchine, loc. cit.

† Segre, B., Duke Math. J. 12 (1945), 337–65.CrossRefGoogle Scholar An example is

for integral n.

* O(0, 0) is not an inner point of

† See diagram. is bounded by the thick line.