Some years ago Evelyn and Linfoot found an asymptotic formula, with estimation of remainder, for the number of representations of a large integer n as the sum of s r-free integers. For s ≥ 4 their formula was subsequently sharpened by Barham and Estermann, and for s = 3 recently by me.

Let θ > 0 and α ≠ 0 be real numbers, and let θ be irrational. Khintchine has shown, by the use of continued fractions, that there is an infinite number of pairs of positive integers (p, q) which satisfy the inequality

for any given K > 5−½; and, more recently, Jogin has shown the same is still true with K = 5−½. The condition that p and q shall be positive is, of course, essential, as otherwise there is the classical result K = ¼ due to Minkowski.

1. Let

where a > 0, be an indefinite quadratic form, so that d = b2 − 4ac > 0. A classical theorem of Minkowski states that, if (x0, y0) is any pair of real numbers, there are numbers (x, y) congruent (mod 1) to (x0, y0), such that

and, more recently, Davenport has shown that this theorem can be sharpened for certain special f, for instance that it is always possible to satisfy

In this paper, all numbers are real and all radicals are positive.

Let f(x, y) = ax2 + bxy + cy2 be an indefinite quadratic form, and let d = Δ2 = b2 − 4ac, where Δ > 0. A well-known theorem of Minkowski states that, if (x0, y0) is any pair of numbers, then there exists a pair (x, y), x ≡ x0 (mod 1), y ≡ y0 (mod 1), say (x, y) ≡ (x0, y0) (mod 1), such that

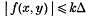
for k ≥ ¼, and Davenport has shown how this result may be improved if we know a value assumed by f(x, y) for coprime integral values, (x, y) = (m, n) ≠ (0, 0). In this paper, we discuss the more general inequality

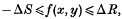
where R and S are constants, and use the method developed in the first paper of this series to obtain a sharper and more general theorem than Davenport's. We give an application to the theory of real Euclidean quadratic fields and to a problem in Diophantine approximation discussed by Khintchine.

In a previous joint paper (‘The dissection of rectangles into squares’, by R. L. Brooks, C. A. B. Smith, A. H. Stone and W. T. Tutte, Duke Math. J. 7 (1940), 312–40), hereafter referred to as (A) for brevity, it was shown that it is possible to dissect a square into smaller unequal squares in an infinite number of ways. The basis of the theory was the association with any rectangle or square dissected into squares of an electrical network obeying Kirchhoff's laws. The present paper is concerned with the similar problem of dissecting a figure into equilateral triangles. We make use of an analogue of the electrical network in which the ‘currents’ obey laws similar to but not identical with those of Kirchhoff. As a generalization of topological duality in the sphere we find that these networks occur in triplets of ‘trial networks’ N1, N2, N3. We find that it is impossible to dissect a triangle into unequal equilateral triangles but that a dissection is possible into triangles and rhombuses so that no two of these figures have equal sides. Most of the theorems of paper (A) are special cases of those proved below.

1. We write L for the class of integrable functions in (− ∞, ∞), V for the class of functions of bounded variation, and define A, A to be the classes of functions F(x) which may be expressed in the forms

respectively.

This paper is devoted to the classical problem of surfaces of minimum area subtending a given closed contour.

If h(r, θ) is harmonic in the unit circle | r | < 1 and satisfies the condition | h | ≤ 1, then there is a function u(ø) which satisfies | u | ≤ 1 such that

and conversely. Hence, any properties of such harmonic functions should be deducible from equation (1). A number of such properties have been proved by Koebe (Math. Z. 6 (1920), 52–84, 69), using Schwarz's lemma and the geometry of simple conformal transformations. They can be deduced from (1) together with an elementary lemma on the rearrangement of a function (Lemma 1 below). As, however, students of this subject will regard Koebe's method as the one best adapted to establish his theorems, we shall illustrate the alternative method by considering two new problems, namely to find max ∂h/∂r, max ∂h/∂θ, where the maximum in each case is taken for all harmonic functions h which satisfy

1. In a recent paper (1) the reflexion of surface waves by a submerged plane barrier has been considered, and it has been shown that there is a reflected wave of finite amplitude at a great distance from the barrier, so that the coefficient of reflexion (the ratio of the amplitudes, at a great distance from the barrier, of the reflected and incident waves) is finite. In this paper it is shown that in the case of reflexion by a submerged circular cylinder, the coefficient of reflexion is zero, with the result that the only effect of the obstacle at a great distance is that there is a phase-difference between the incident and transmitted waves, their amplitudes being the same. Only one case has been worked out in detail numerically, and the method employed is such that the condition that the section of the cylinder must be a stream-line has been satisfied only to an approximation; it is, however, shown that the coefficient of reflexion is zero in the general case.

1. The problem to be discussed in the present paper arises when the finite resolving time of a recording apparatus is taken into account. Events are divided into two classes, recorded and unrecorded. Any recorded event is followed by a dead interval of a certain length of time, during which any other event which occurs will be unrecorded. A typical example is an α-particle counter; a recorded particle causes the chamber to ionize, and no other particle can be recorded until the chamber has deionized. In the case when the dead interval is of constant length τ, if the observation time t lies between (n − 1)τ and nτ, the number of recorded events must be 0, 1, 2, …, n − 1 or n. We shall assume that the probability of an event occurring in the interval [t, t + dt] is λdt, λ being constant; this is the case of most practical interest. The probability distribution of recorded events for dead intervals of constant length has been determined by Ruark and Devol (2). The explicit expression of this distribution is fairly complicated, and it is therefore difficult to manipulate. The method employed in the present paper leads naturally to the Laplace transform of the distribution with respect to the time t, and this is relatively simple. The method can easily be generalized to deal with the case of dead intervals which are not all equal, but follow a probability distribution u(τ) dτ. Finally the Laplace transform is very convenient for determining the asymptotic behaviour of the distribution of recorded events for large times of observation.

1. We recall the meaning attributed by F. Hausdorff to the statement: ‘The (linear) set S is of dimension [h(x)].’

In this paper we investigate the following problem.

We suppose given a sequence of complex values wn, defined for n = 0, 1, 2, …, and for n = ∞, and such that

while at least one wn differs from zero and ∞. We consider functions f(z), which are regular in | z | < 1, and take none of the sequence of values wn, and we investigate the effect of this restriction on the rate of growth of the function, as given by the maximum modulus

A rubber molecule containing n + 1 carbon atoms may be represented by a chain of n links of equal length such that successive links are at a fixed angle to each other but are otherwise at random. The statistical distribution of the length of the molecule, that is, the distance between the first and last carbon atoms, has been considered by various authors (Treloar (1) gives references). In particular, if the first atom is kept fixed at the origin of a system of coordinates and the chain is otherwise at random, it has been conjectured that the distribution of the (n + 1)th atom will tend, as n increases, towards a three-dimensional normal distribution of the form

where σ depends on n. Thus r2 (= x2 + y2 + z2) will be approximately distributed as σ2χ2 with three degrees of freedom.

The general linear difference-differential equation takes the form

where x is a real variable, ν(x) and Aμν(x) are known functions and

1. The problem of determining the distribution of stress in a semi-infinite solid medium when its plane boundary is deformed by the pressure against it of a perfectly rigid cone is of considerable importance in various branches of applied mechanics. It arises in soil mechanics where the cone is the base of a conical-headed cylindrical pillar and the semi-infinite medium is the soil upon which it rests (1). In this instance the distribution of stress in the soil is known to be more or less similar to that calculated on the assumption that the soil is a perfectly elastic, isotropic and homogeneous medium, at least if the factor of safety of a mass of soil with respect to failure by plastic flow exceeds a value of about three (2). The same problem occurs in the theory of indentation tests in which a ductile material is indected by cylindrical punches with conical heads (3).

1. The problem investigated in this note was suggested by a study of the mathematical basis of change ringing. Its campanological application is discussed in § 4.

Bagnera(1) shows that when a certain primitive finite group of order 576, G576, is represented as a group of collineations in three-dimensional space, it contains twenty-four harmonic inversions with respect to points and planes, and he shows how to calculate the coordinates of the points and planes of the inversions. The purpose of this note is to discuss the configuration of these points, which we shall call vertices, to show that the whole group is generated by the twenty-four harmonic inversions, termed projections after Prof. Baker (2) and Dr J. A. Todd (4), and to enumerate the conjugate sets of the group.

In the dynamical theory of the motion of the Earth relative to its centre of mass, the planet is usually regarded as a rigid or at most only slightly deformable body, and moments of inertia are adopted that are taken to refer to the Earth as a whole, while the motion itself at any instant is assumed capable of representation by a single angular velocity vector. This procedure, however, appears to involve unwarranted assumptions the recognition and removal of which may lead to conclusions of considerable importance. For it is well known from the theory of earthquake waves that the material of the central core of the Earth behaves like a liquid in that it transmits only longitudinal wave vibrations, while there is also other evidence suggesting that the material of the core is a true liquid (1). There is accordingly no a priori reason for supposing that the core will behave like a rigid body firmly attached to the surrounding shell if more or less permanent shearing forces are applied to it. In particular, in respect of any couple known to act on the outer shell, it is not permissible to assume, without examination of the assumption, that its effect will be transferred immediately to the inner core in a way preserving rigid-body rotation of the whole. If the material of the core behaves like a liquid where wave-motion is concerned, this suggests that it will probably also behave like a liquid whatever shearing forces act on it, and the extent to which changes in the rotatory motion of the outer shell can be communicated to the core, and what effects direct gravitational forces acting on the core may have, must in the first instance be questions of hydrodynamics and not rigid dynamics.

It is shown that under certain conditions convective flow may occur in fluid which permeates a porous stratum and is subject to a vertical temperature gradient, on the assumption that the flow obeys Darcy's law. The criterion for marginal stability is obtained for three sets of boundary conditions, and the motion described. If such convection occurs in a stratum through which a bore-hole passes, the usual method of calculation of the heat flow must be modified, but in general the correction will not be large.

The two previous papers of this series dealt with the determination of the complete system of combinantal covariants and contravariants of a pencil of quadric surfaces. The present paper is concerned with combinantal forms involving line-complexes, and with certain syzygies which exist between these forms. It is essentially a preparation for the determination of the complete system of combinantal line-complexes of the pencil, which will be carried out explicitly in the next paper of the series.