If f is a real, indefinite, binary quadratic form of discriminant d and if κ(f) is the minimum of | f | taken over all integer values of x, y, not both zero, then it is well known that and that this is a ‘best possible’ result.

A possible degree of heterogeneity in the structure of continua is investigated in this paper.

The Vitali covering principle is a powerful method in a wide class of problems of the theory of functions of a real variable and of the theory of sets.

Let γ be an irreducible variety of dimension d, and let In denote an involution of order n on Γ. The image of In is a variety C, also irreducible and of dimension d, and Γ is said to be a multiple of C. Among the possible multiples of a given variety C there is a class of particular interest; this arises when the involution In possesses the following properties:

(1) it is unramified, that is, in every set of the involution the n points are all distinct;

(2) it is generated by an Abelian group G of order n of birational transformations of Γ into itself. Given any point P of Γ the n transformations of G transform P into n points P1 = P, P2, …, Pn which constitute a set of In. The two conditions together imply that the function field κ of Γ is an unramified Abelian Galois extension of the function field k of C, and this shows that the study of the particular class of multiple varieties—which we may call normal multiple varieties when it is necessary to give a name to them—is analogous to the study of a well-known branch of the theory of numbers.

In this note I consider the Abelian integrals of the first kind on an algebraic curve Γ which is a normal multiple of a curve C, as defined in Note I*.

1. In the complete algebraic system of concomitants of a pair of quaternary quadrics given by Turnbull† there appear sixteen covariant line-complexes, eight of the second order and eight of the third. In a later paper‡, the same author gave some geometrical interpretations of these and other concomitants. None the less, no systematic geometrical account of the relations of these complexes seems to have been made. The purpose of the present paper is to discuss the geometrical relations systematically, and make their origin clearer. Incidentally, the syzygies which exist between the complexes are obtained explicitly.

Attempts have been made to extend to higher dimensional varieties the theory of correspondences developed for algebraic curves. So far efforts have been concentrated on ‘point-point’ correspondences (i.e. between two varieties of the same dimension such that a generic point of one corresponds to a 0-dimensional variety of the other), and even in the case of surfaces important problems, such as the base number for the correspondences, are still unsolved (cf. Hodge(3)). The purpose of these papers is to draw attention to, and study in the simpler cases, another class of correspondences, the ‘point-primal’ type, in which to a generic point of one variety corresponds a primal of the other. These correspondences provide at least as natural a generalization of the theory for curves as point-point correspondences, but have so far only been touched on by Severi(7, 8) in two simple cases. In this paper we give a number of general results for point-primal correspondences (mostly immediate generalizations of Severi's results), and embark on a detailed discussion of such correspondences, which we naturally call point-curve correspondences, between two surfaces, the chief result being the determination of the base in that case. Further results on the transformation of the cycles of a surface by a point-curve correspondence, the correspondences induced between curves of the two surfaces and, in the case where the surfaces coincide, the ‘united curve’ of the correspondence, as well as the question of correspondences of non-zero valency, will be dealt with in a later paper, where we shall also consider the case of correspondences between a curve and a surface discussed in Severi's paper(7).

In the present note, which is introductory to the following paper, closed expressions, suitable for computational purposes, are found for the sums of the series

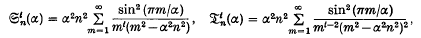
where α > 1, t = 1, 2, 3, …, and n is a positive integer. In each case a recurrent relation is found giving the values of 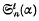and 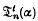for t > 2 in terms of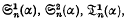 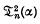and the series Θκ(α) (κ = 1, 2, …, t), where

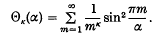
When κ is even the last series is expressed in closed form in terms of the Bernoullian polynomial φκ(l/α) and, when κ is odd and α is rational, a closed form is found involving the polygamma function Ψ(κ)(z), where 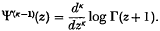The general expressions for 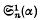and 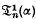involve Ψ(z) and Ψ′(z) when α is rational, but for special values of α they reduce to a form independent of the Ψ-function. 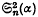and 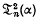are independent of n and are expressible as simple rational functions of α.

In this paper, using the results of the preceding paper, I develop a modification of Hahn's method (1) for calculating the electromagnetic field inside a type of axially symmetric resonator. A process of successive approximation is given for solving the equation which leads to the resonant wave-length λ, both in the case where all the resonator parameters are given and we wish to find λ, and also in the case where λ is given and one of the parameters (the outer radius) is to be found. Some numerical results are given.

1. The present paper deals with an enclosed (linear) harmonic oscillator. The usual boundary condition that the wave function vanishes at infinity is here replaced by the condition that the wave function vanishes at the walls of the enclosure. The problem has been treated before (1, 2, 4). However, the present discussion goes much further than that given in the papers cited*.

The Schrödinger equation for a ‘hole’ in the hole-theory of liquids is constructed and solved by the B.W.K. method. The energy levels are found to be discrete, and the eigenvalues are obtained in terms of the density and surface tension of the liquid. The relation between the energy of the ground state and the temperature of melting is considered.

1. In Dirac's classical theory of radiating electrons, the relativistic equations of motion of a point-electron in an electromagnetic field are

where (x0, x1, x2, x3) denote the electron's coordinates in flat space-time, dots denote differentiation with respect to the proper time , and the external electromagnetic field is described by the usual field quantities Fμν. The units are chosen so that the velocity of light is unity. These equations, which are derived from the principles of conservation of energy and of momentum, are the same as those obtained by Lorentz, when he used the spherical model of the electron and included radiation damping in an approximate way. But Dirac's method of derivation suggests that this treatment of radiation damping, and therefore the resulting scheme of equations, is exact within the limits of the classical theory.